The main features of bubble creation in the parallel surface facing downward
The idea of forming bubbles on inclined surfaces is a crucial one in the engineering processes such as the metallurgical process, nuclear reactor cooling, and the process of submerging gas injection in liquid metal. Besides this, it is also widely used in pharmaceutical procedures. A major application is in Aluminium production in the Hall-Heroult cell where the bubbles are formed on vertical surfaces [1,2]. The bubble’s thickness is an important factor in this process since it reduces the distance between negatively charged and positively charged electrodes and increases the resistance in the current flow. Bubble formation in parallel and inclined surfaces differ, but in both cases, the conduct of the bubble is to a great extent affected by the force of gravity among other factors such as low rate of motion, buoyancy, surface pull, and viscosity. These factors change in relation to the stage of bubble development. The physical appearance of the bubble is also important in that it affects the speed of flow in the liquid. From this, therefore, it is clear that sufficient knowledge in this subject is required if the Hall-Heroult cell production process is to be carried out successfully in an industrial setup.
A study has been carried out on bubble formation using a vertical surface with hydrokinetics of the same process in the horizontal platform in consideration [3]. It needs a thorough understanding of the physical shape of the bubbles and their relation to the speed of apparatus inside the sloping walls. This mechanism of using sliding planes on rising bubbles was reported by Maxworthy [4]. This ensures that the physical appearance and speed of bubbles inside water on both sloping and parallel planes with temperatures ranging between 5 and 90 degrees were experimented on. The effect of inclination and size of the tunnel on the speed at the terminal of large bubbles going beneath the surface has been proven experimentally by Chen et al. [5] and Che et al. [6]. In this experiment, the bubbles are developed by using a syringe to push predetermined amounts of air into a small container that is facing downwards and the outcome of the inclination on preset volume bubbles is determined. These results can be verified by using different diameters of between 2 and 5 millimeters and varying rates of flow in the injection of between 18ml/s and 166ml/s. a number of studies [3,7,8] have been carried out on temperature transmission related to the sloping bubbles. Addlesse and Cornwell made attempts to determine how thick the liquid film becomes when the bubbleheads towards the sloping surface.
Lubrication theory [7] is an assertion put across to explain the film in between the movement of the bubble and the wall of the cell. Much heat is transmitted when the bubbles are moving and this affects the thickness of the film especially when bubble is moving on a sloping surface Pushkarova and Horn [10]. Peng et al. [11] developed a measure experimentally to determine the surface push between the wall and the bubbles being formed. The result of this is a numerical representation of the predictions for the physical appearance and mass of the bubbles beneath the parallel platform. Perron et al [1] explained that the bubbles are formed in round shapes but due to the force of gravity, they flatten with time. There are two phases in which the bubbles go through, the first one being the enlargement phase and the second one being the separation phase [12]. This is however not the case in platforms that are facing downwards since here the force of gravity aides bubble growth and instead of separating, the bubbles either spread on the plane or inclination depending on what was used. When developing the circular shape, the bubbles remain attached to the plunger while at the same time maintaining contact with the surrounding of the opening. Here, the famous Laplace equation is used to determine the physical appearance of the interface at the point of stability. When applied in real-life processes such as the Hall-Heroult cell, in which case the distance between the positively and negatively charged electrodes is small, the size of the bubbles and their developing characteristics affect the flowing feature of the liquid metal.
Bubble formation and thickness
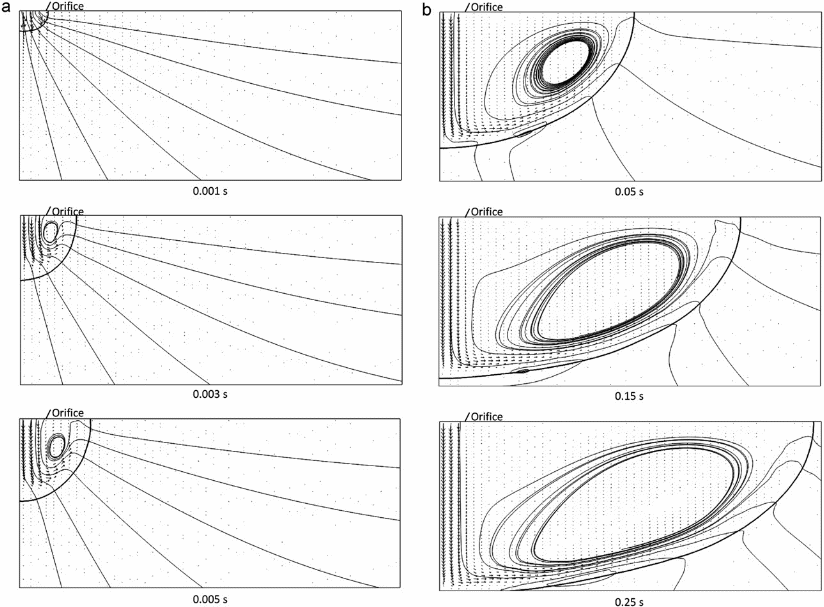
Here, the numerical outcomes arrived at using the phase-field analysis and are discussed below. The outcomes are derived from openings of different diameters which in this case are, 0.001m, 0.002m, and 0.003m. Together with the varying rates of gas injections into the liquid with a concentration of 996 kg/m3 and resistance of 1.0e-3 Pa-s the results indicated by the above figures are arrived at. Varying levels of surface pull (between 0.040 and 0.072 N/m) are also employed in this computation. Fig. 10 illustrates a forecasted phase-field value denoted as ϕ and this symbolizes the bubble platform. The resistance and speed in these two stages are graphed at different times of the experiment so as to obtain the exterior tension shown by σ = 0.072 N/m, assuming an opening diameter of 0.001m and rate of air insertion at 0.35ml/s. The radius streamlines on the outside and is shown by t at 0.001s. This is an indication of the bubble’s growth and development of a circular shape. When the air is flowing, swirls are created the moment the bubble becomes bigger than the diameter of the opening, interfering with the spherical shape.
The bubbles size grows at a fast rate and this shows a serious change in the width–height ratio. Despite this, it begins to flatten once it has obtained its optimum size since the gravitational force cannot allow it to continue growing. The top of the flattened bubble begins to accumulate a significant amount of static air because a tangential motion is experienced at the bottom, emanating from the rate of gas flow. At this point, thickness remains fixed while the base increases as shown in Fig. 10b.
Bubble growth curve
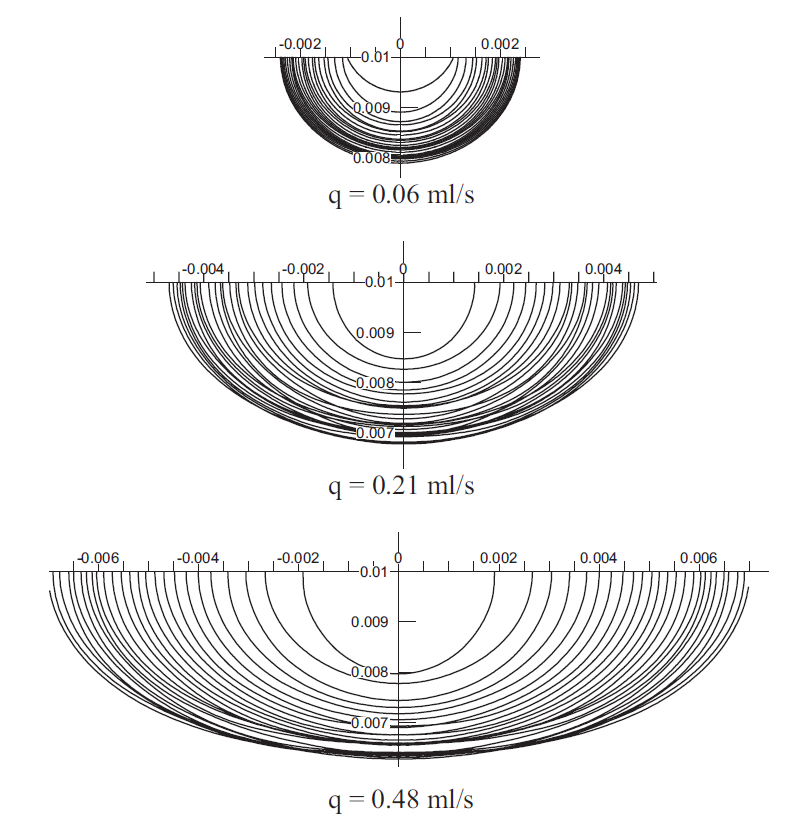
These curves in Fig. 11 are developed at a diameter of 0.002m and injection rates that differ. The rate of bubble growth and gas flow changes proportionately while the thickness changes inversely.
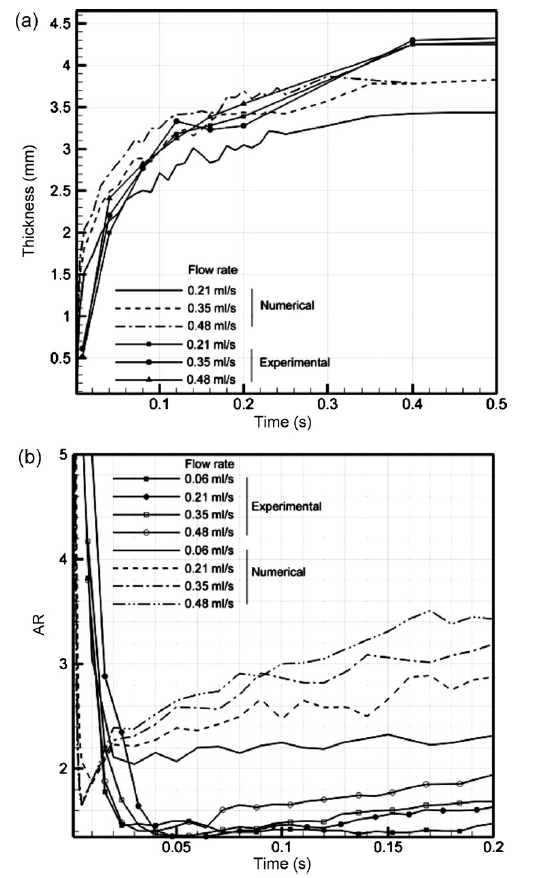
In these two illustrations, it can be deduced that the bubble’s thickness grows and reaches an optimum point after some time. This is dependent on the opening’s diameter and the speed of gas flow. The change in width – height ratio against time is equated to the obtained data and the result is similar to that observed at the beginning of the bubble development phase (Fig. 12b). An observation is made from the experiment which shows that the bubble develops in a circular shape then flattens at a point when the diameter exceeds that of the opening as a result of platform inclinations.
(σ = 0.072 N/m).
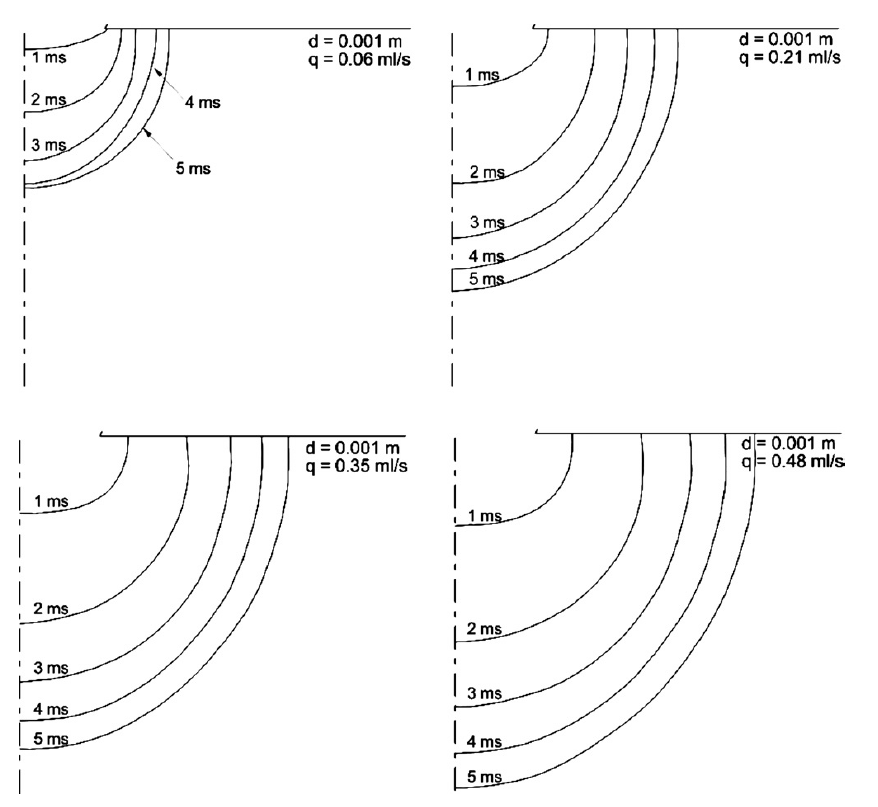
The above illustration indicates numerical outcomes of bubble growth at the beginning of the formation inside water i.e. during the first 5 ms, are compared and discussed. Fig. 13 indicates the mathematical results with differing rates of air insertion ranging from 0.06 to 0.48 ml/s and an opening diameter of 0.001m. The lines are drawn at different periods whereby the change in time is denoted by Δt = 1ms. The force of gravity affects the bubble’s physical appearance right from the beginning up to the time it gets under the parallel surface. The bubble maintains its circular form as a result of surface pull from the time it appears at the opening and the flattening phase is a result of gravitational force.
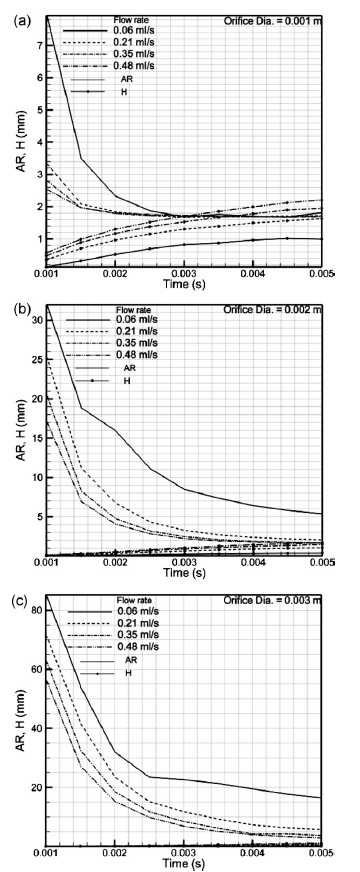
Fig 14 indicates how the opening diameter and rate of gas injection affect the change in weight–height ratio at the beginning of the process and this is blamed on the large alteration in width – height ratio. It is therefore anticipated that the flow brought about by the bubble movement should be significant. As the bubble grows, the chance of an increase in weight–height ratio diminishes since the bubble no longer thickens. Once the bubble is large, the rate of growth reduces as a result of the stabilized flow of air but this has an insignificant influence on the water surface.