Quality Control System for Typesetters and Calculation Case Study

Exclusively available on Available only on

Typing pool

Part a

This section will entail the construction of process control limits for a typing pool. The first stage entails computing the sample proportion for each of the values in the sample. The value is arrived at by dividing the number of defective items by the sample size. The sample proportion is presented in the table below.

Sample	N	Defective	Proportion defective
1	400	4	0.01
2	400	8	0.02
3	400	8	0.02
4	400	0	0.00
5	400	4	0.01
6	400	12	0.03
7	400	8	0.02
8	400	4	0.01
9	400	0	0.00
10	400	16	0.04
11	400	12	0.03
12	400	8	0.02
Total	4,800	84	0.21

The second step entails calculating the average of the sample proportion. The average is arrived at by dividing the total number of defective by the total number of observations in the sample. The calculations are shown below.

ṗ = 84 / 4800 or 0.21 / 12

= 0.0175

The third step entails calculating the standard deviation of the sample proportion. The formula for calculating the standard deviation is presented below.

Sp = √ [ṗ (1 – ṗ)] / n

= √ [0.0175(1 – 0.0175)] / 400

= √0.000042984375

= 0.006556

Upper control limit = p + 3 s_p

= 0.0175 + (3 * 0.006556)

= 0.0175 + 0.019669

= 0.03717

Lower control limit = p – 3 s_p

= 0.0175 – (3 * 0.006556)

= 0.0175 – 0.019669

= -0.002169

Therefore, the control limit for the p-chart lies between (0.002169) and 0.03717. This implies that if all the values of sample proportion fall within the range, then the process is considered to be in control. However, if some values lie outside the p-chart range, then the process is considered to be out of control.

P –control chart

The graph presented below shows the process control chart for the typing pool.

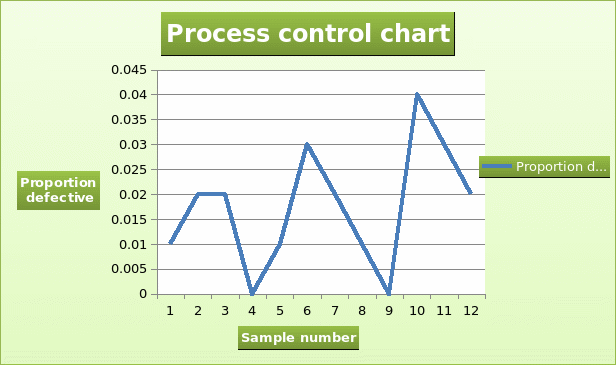
Thus, it can be noted that only one point (0.04) lies outside the control limit. It lies above the upper control limit. Thus, it can be concluded that the process is not in control. This implies a sample of 12 from 400 letters will yield only one defective.

Part b

The sample proportion for a sample of six from 400 letters is calculated as shown below.

ṗ = 6 / 400

= 0.015

From the previous calculations, the upper control limit was 0.03717 while the lower control limit was (0.002169). Thus, a value of 0.015 falls within the upper and lower control limits. This implies that the process will be in control when a sample of 6 letters is picked.

Question 2: Robin Hood Bank

This section will entail calculating control limits for the x-bar and R-chart for the bank.

Part a: control limits for x-bar and R-charts

Average daily demand deposit balance = $109 million (It represents the sample of all the sample averages.)

Average range = $15 million (It represents the average of all the sample ranges.)

X – Bar

Control limit (CL) = 109 million

The value of A₂ is read from a table. A section of the table for A₂ is presented below.

Subgroup size	A₂
2	1.880
3	1.023
4	0.729
5	0.577
6	0.483

Therefore, from the table, the value of A₂ is 0.483.

Upper control limit (UCL) = 109 + 0.483 (15)

= 116.245 million

Lower control limit (LCL) = 109 – 0.483 (15)

= 101.755 million

Based on the calculation, the control limit for the x-bar lies between 101.755 million and 116.245 million. Thus, values that lie outside the x-bar control limit will make the entire process be out of control.

R – Chart

Control limit = 15

The values of D3 and D4 are read from a predetermined table. A section of the table is presented below.

Subgroup size	D₃	D₄
2	0	3.268
3	0	2.574
4	0	2.282
5	0	2.114
6	0	2.004

Thus, the value of D3 and D4 are 0 and 2.004 respectively.

Upper control limit = 0 (15)

= 0

Lower control limit = 2.004 (15)

= 30.06 million

Based on the calculation, the control limit for the R-chart lies between 0 million and 30.06 million. Values that lie outside the range make the whole process to be out of control.

Part b: average and range

The calculation for the average demand deposits for the past six days is presented below.

= (110 + 102 + 96 + 87 + 115 + 106) / 6

= 616 / 6

= 102.67 million

The calculation for the range of the demand deposits for the past six days is presented below.

= 115 million – 87 million

= 28 million

The average of the sample of the past six days is 102.67 million. It lies within the upper and lower control limit for the X-bar. Further, the range of the sample collected in the past six days is 28 million. The range also lies within the upper and lower control limit for the R-chart. Thus, the management needs to continue with the production process because there is no alert for an assignable cause.

Question 3

α = 0.1 (all values are corrected to 2 decimal places)

Day	Demand (D_t)	F = F_i+ 0.1(Ai – F_i)		D_t– F	\|D_t– F\|
1	200	=100 + 0.1(200 – 100)	110	90	90
2	134	=110 + 0.1(134 – 110)	112.4	21.6	21.6
3	147	=112.4 + 0.1(147 – 112.4)	115.86	31.14	31.14
4	165	=115.86 + 0.1(165 – 115.86)	120.77	44.23	44.23
5	183	=120.77 + 0.1(183 – 120.77)	126.99	56.01	56.01
6	125	=126.99 + 0.1(125 – 126.99)	126.79	-1.79	1.79
7	146	=126.79 + 0.1(146 – 126.79)	128.71	17.29	17.29
8	154	=128.71 + 0.1(154 – 128.71)	131.24	22.76	22.76
9	182	=131.24 + 0.1(182 – 131.24)	136.32	45.68	45.68
10	197	=136.32 + 0.1(197 – 136.32)	142.39	54.61	54.61
11	132	=142.39 + 0.1(132 – 142.39)	141.35	-9.35	9.35
12	163	=141.35 + 0.1(163 – 141.35)	143.52	19.48	19.48
13	157	=143.52 + 0.1(157 – 143.52)	144.87	12.13	12.13
14	169	=144.87 + 0.1(169 – 144.87)	147.28	21.72	21.72
		Total		425.51	447.79

α = 0.3

Day	Demand D_t	F = F_i+ 0.3(Ai – F_i)		D_t– F	\|D_t– F\|
1	200	=100 + 0.3(200 – 100)	130	70	70
2	134	=130 + 0.3(134 – 130)	131.2	2.8	2.8
3	147	=131.2 + 0.3(147 – 131.2)	135.94	11.06	11.06
4	165	=135.94 + 0.3(165 – 135.94)	144.66	20.34	20.34
5	183	=144.66 + 0.3(183 – 144.66)	156.16	26.84	26.84
6	125	=156.16 + 0.3(125 – 156.16)	146.81	-21.81	21.81
7	146	=146.81 + 0.3(146 – 146.81)	146.57	-0.57	0.57
8	154	=146.57 + 0.3(154 – 146.57)	148.80	5.2	5.2
9	182	=148.8 + 0.3(182 – 148.80)	158.76	23.24	23.24
10	197	=158.76 + 0.3(197 – 158.76)	170.23	26.77	26.77
11	132	=170.23 + 0.3(132 – 170.23)	158.76	-26.76	26.76
12	163	=158.76 + 0.3(163 – 158.76)	160.03	2.97	2.97
13	157	=160.03 + 0.3(157 – 160.03)	159.12	-2.12	2.12
14	169	=159.12 + 0.3(169 – 159.12)	162.08	6.92	6.92
		Total		144.88	247.4

Thus, exponential smoothing with α = 0.3 provide better results than α = 0.1.

More related papers