Commonly Used Heuristics in Resource Allocation Essay

Finding solutions to resource preparation problem for most favorable response is exceedingly complicated, especially for the big project networks with several distinct resource types. Nevertheless, according to Akanda’s presentation of heuristics in project management, many heuristics are present to tackle such difficulties. According to the YouTube video presentation, these heuristics assign resources to activities to reduce project postponement based on some priority principles (Akanda et al). The two mostly applied heuristics are the serial and the parallel methods.

Akanda evidently states in the video presentation that in the serial technique of resource distribution, activities are arranged into a list and resources distributed to each of the bustles one at a time in anticipation of resources distributed to all activities. The parallel technique on the other hand, has resources distributed on an interval basis other than each activity. In this technique, only those actions whose previous activities have been accomplished will be taken into consideration (Balas 189). If two or more actions vie for same possessions, then distribution of the possessions is centered on certain stipulated main concern principles. Akanda clear states in the video that when parallel heuristic is compared to serial, there is no doubt that the parallel technique is the most widely used heuristic (Akanda et al). Below are examples of main concern principles provided by Akanda in the video, in order presented that are most influential in project postponement.

• Smallest time period
• Minimum slack
• Lowest action identification number

Despite these preoperational heuristic applied, the main impact of resource limitation scheduling is the defeat of flexibility because of the minimization of slack as observed in the YouTube presentation. He added on that the minimization in slack also raises the number of significant or close to significant activities. In order to understand the concept of the two majorly used heuristics, the following details are provided.

The Serial Method

According to the video presentation, Kelly (1963) suggested the serial technique, which consists of n=1…..j stages, whereby every activity is chosen and scheduled. Related to each of the two stages are two put out of place activity-set. Tutor Akanda clearly states in the presentation that in the schedule set S_n are the actions, which were already in program and therefore belong to the fractional program (Balas 190). The decision group, D_n encloses the un-programmed actions with each precursor being in the program set. He adds on that in every stage, one action from the decision group is picked with a main concern rule (when ties occur, the actions with the smallest action number is picked) and programmed at its premature precursor and resource practicable start time. Thereafter, the picked action is eliminated from the.determination set and included in the programmed set. This as a result, may put a number of actions into the determination set, because all their precursors are now programmed (Akanda, lecture 15).

The algorithm ends at stage number n=j, where all actions are in the fraction program i.e. the scheduled set. Tutor Akanda went on to suggest in the YouTube presentation that in order to issue a formal account of the serial programming method, some extra notation has to be commenced. Let 7rK_rt be the left over size of the renewable possession r in period t, and D_n the determination set, be described as follows (Akanda, lecture 15)

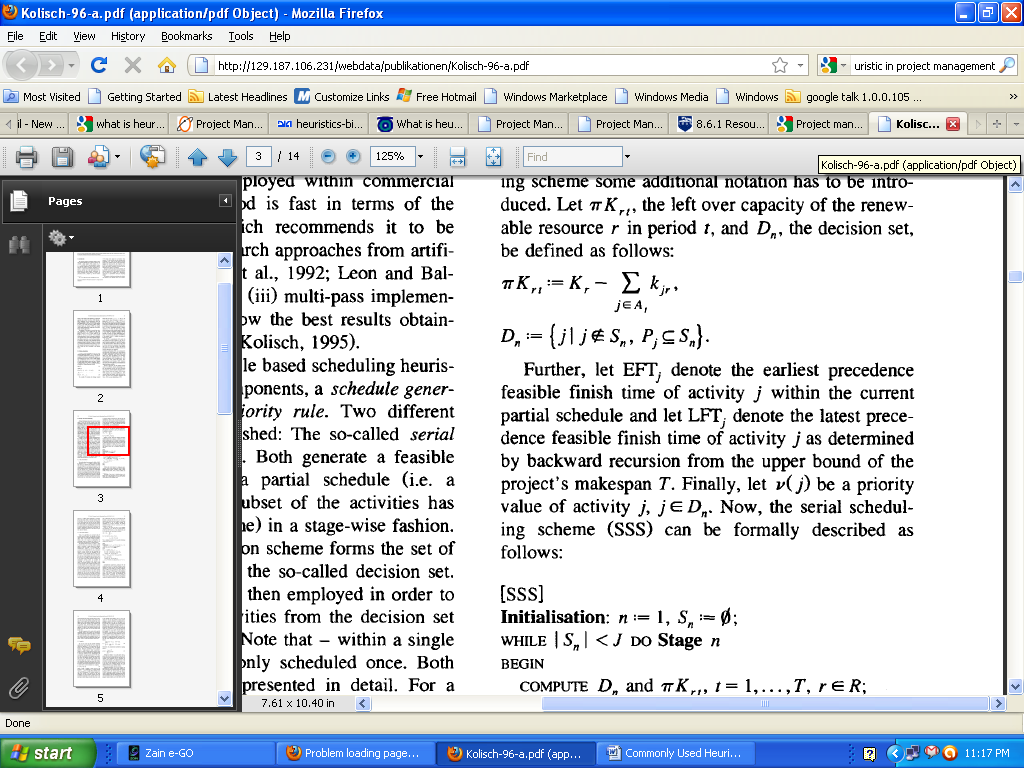
Moreover, let EFTj stand for the initial precedence feasible complete time of actions j within the running fraction program and let LFTj stand for the latest precursor feasible complete time of action j as determined by rearward recursion from the upper leap of the project’s make span T. (Akanda, lecture 15). Lastly, let v(j) be a main concern figure of action j, j ED_n. Now, the serial Scheduling scheme (SSS) can be once defined as follows;

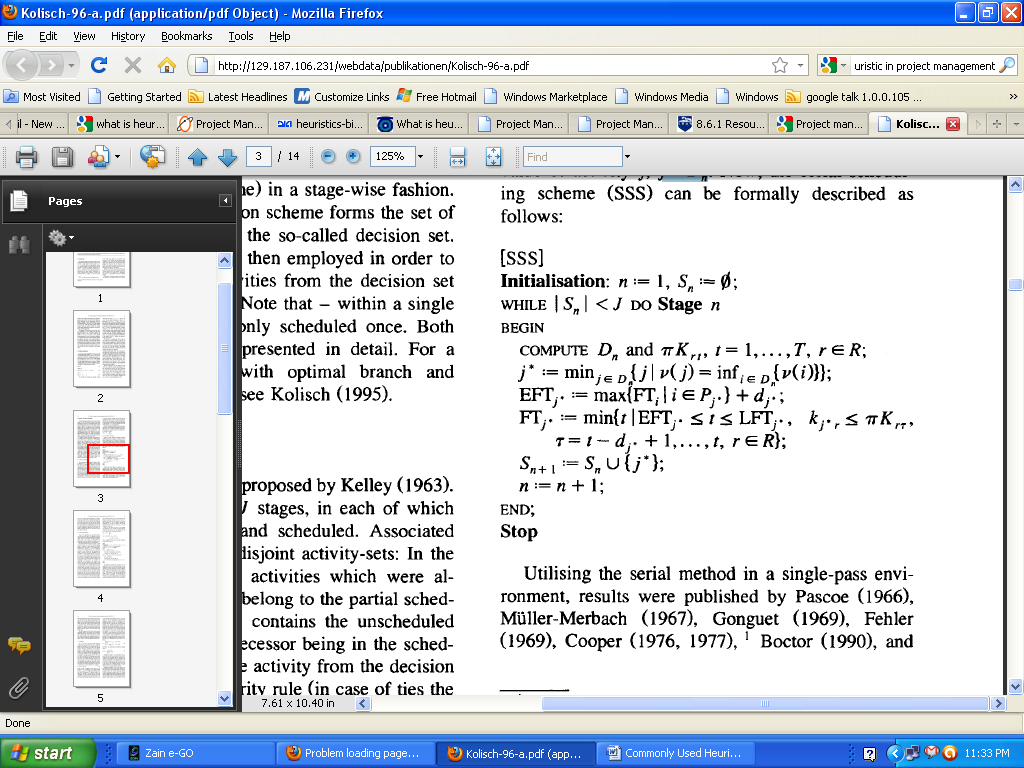
The YouTube presentation clearly indicates that there was a computational research carried out by Boctor based on 36 little examples from literature. The two finest main concern rules used in his research picked the action with the smallest final intersection number in an action-on-arrow network. Bondages were sorted out by programming the activity with the least initial joint and with the highest total possession requirement, respectively (Balas 194). Both principles acquired an average rise of 9.13 percent above the most favorite objective operation. Therefore, it is evident enough in the presentation that serial scheme, activities are arranged into a list and resources distributed to each of the bustles one at a time in anticipation of resources distributed to all activities.

The Parallel Method

The parallel technique contains two algorithms; the algorithm of Kelly (1963) and the algorithm of Brooks (Bedworth and Bailley, 1982), which is also referred to as “Brooks algorithm” (BAG) (Akanda et al). Just the way it is in several publications, the programming system as suggested by Brooks is used herein and called parallel method. The presentation clearly states that the parallel technique is made up of utmost j stages in each where a set of actions (which might be blank) is programmed. An exclusive characteristic of the parallel technique is that every stage n is related to a program time t_n where t_m <_ t_n for mholds. On description of this program time, the set of programmed actions is now halved into the following two subsets: actions which were programmed and are accomplished according to the program and they are in the complete set C_n, while actions which were programmed whose program time is still active and running are in the Active Set A_n.

Lastly, there is the decision set D_n. Unlike the serial method, parallel technique contains all but not programmed actions, which are present for programming w.r.t. precursor and resource restrictions. The fractional program of every stage is equivalent to the initial completion time of actions in the active group of the ancestral stage (Akanda et al). Every stage consists of two steps: (1) the new program time is established and actions with a complete time equal to the (new) program time are eliminated from the lively set and included in the finished set. (2) one action from the determination set is picked with a main concern principle (in case of binding together, the actions with the least label is selected) and programmed to begin at the present program time (Balas 197).

Thereafter, this action is eliminated from the determination set and included in the lively set. The second step is done again until the determination set becomes blank that is, actions were programmed or are not available any longer for programming w.r.t. resource restrictions. The parallel technique ends when all actions are in the complete or lively set (Akanda et al). Given A_n, the lively set, and C_n, the complete set, respectively, 7rK_r, remaining period size of the renewable possession r at the program time, and D_n, the decision set, are described as follows (Balas 200):

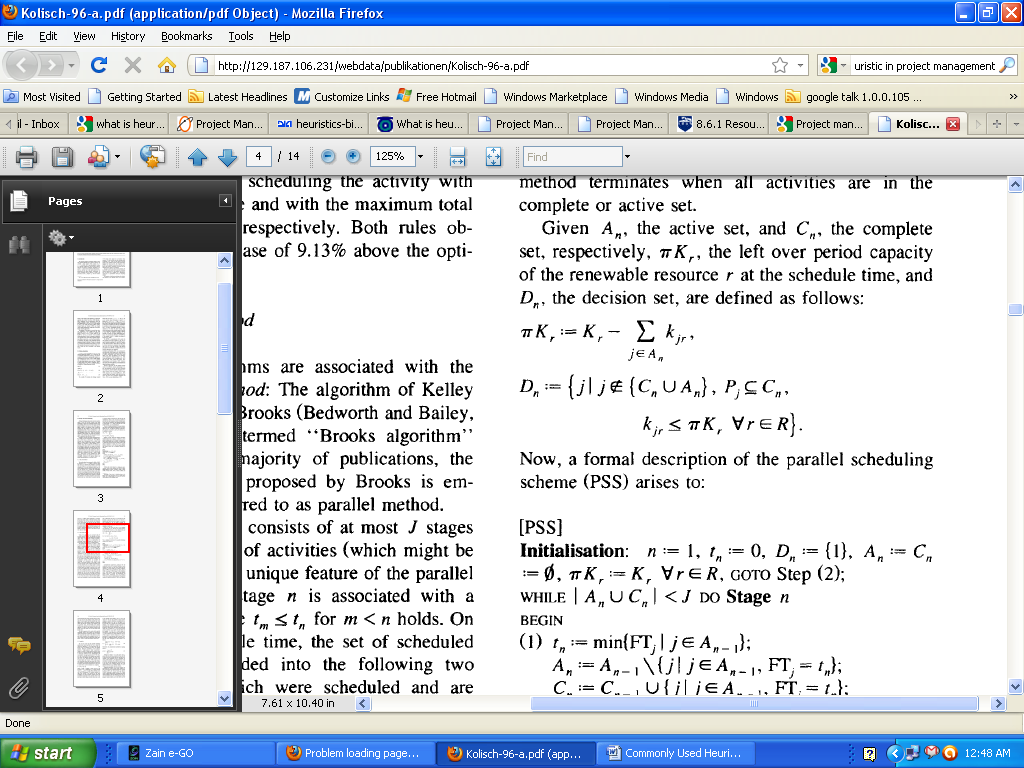
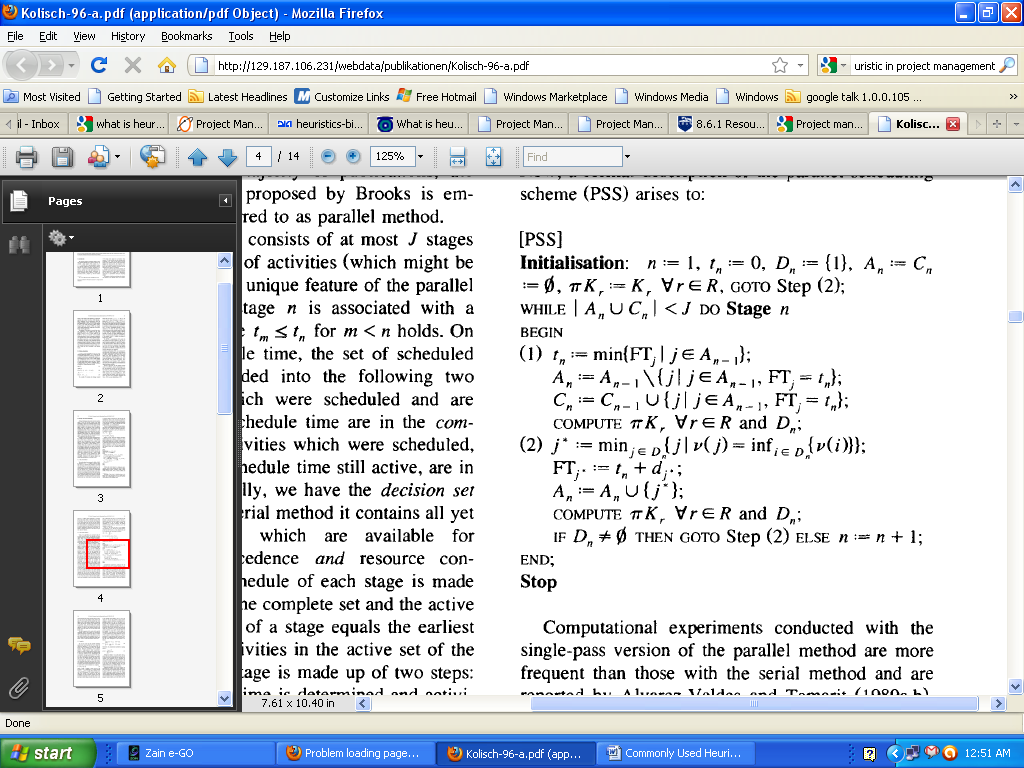
In this case, an official illustration of the parallel scheduling scheme (PSS) arises to:

Reccomendation

I decided to pick on Serial and parallel heuristics methods because they are the best for projects of all types unlike other heuristics such as representativeness heuristic, availability heuristic, anchroing heuristic and similarity heuristic among others. according to Akanda’s youtube presention of heuristics for project management, serial and parallel are the best of all heuristics because they are able to work concurrently and in several different projects where they are able to perform many functions. according to the youtube presention by Akanda, serial and parallel heuristics are important because they are the only ones which can perform the following five key functions:

• Multi-user functionality
• Scheduling function
• Consolidation
• Communication
• Integration

The other heuristics can only perform one or atmost two of the above functions meaning that they are not as efficient as the serial and parallel heuristics. Therefore, it is evident enough that serial and parallel heuristic methods are the best for project management especially in mutiple projeccts where the computation comes out perfectly (Akanda et al). Both of them produces practible schedules that are most favorable in the absence of resource constraints. It was confirmed that the serial technique produces lively programs while the parallel program scheme generates non-delay programs. Both of these programs are efficient and very effective in all types of projects.

Works cited

Akanda, Arun. “Lecture -15 Limited Resource Allocation”. YouTube Video Presentation. 2011. Web.

Balas, Ebru. “Project scheduling with resource constraints”, in: E.M.L. Beale (Ed.), Applications of Mathematical Programming techniques. London: English University Press, 2003. Print.