Although commonly confused with motivation, job satisfaction describes how happy employees are with their job. There are many factors that contribute, either directly or indirectly, to job satisfaction. For purposes of data analysis in this study, I have chosen employee position and extrinsic factors.
Based on data available in this study, position held by an employee is described as hourly employee or salaried employee in which case only the former is eligible for overtime work. This aspect is likely to affect the level of job satisfaction since it places restrictions to employees based on their position ascription. Besides extrinsic factors such as working environment, team members, leadership style at workplace and office location are likely to contribute directly to job satisfaction. I believe these two variables are the most appropriate in this study.
Findings from data examination
Position
Position as represented in this data is a qualitative. Such a data set can only be analyzed using mode to describe the frequency of the distribution (Bartz, 1971). Mean and median are not applicable in this case since this is a coded data set referring to only two situations. For this reason, computation of mean and median will be misleading. Measures of variability are equally not applicable in this case since they are computed from mean, a measure which has already been disputed.
This data set has a mode of 1; meaning that majority of employees interviewed in this study are hourly employees. This shows that most employees are comfortable working as hourly employees with the guarantee of paid overtime as opposed to being salaried employees. Figure 1.1 clearly illustrates these findings.
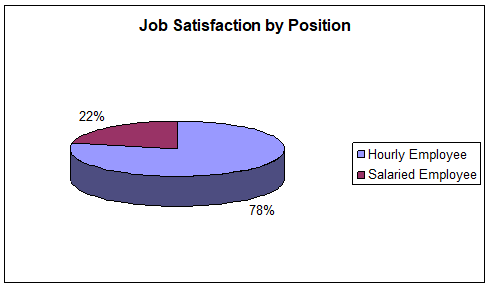
Figure 1.1: Job Satisfaction by Position
Source: Researcher
Extrinsic Job Satisfaction
Extrinsic job satisfaction arises from factors external to the job itself. Extrinsic job satisfaction as represented in this data is a quantitative, hence can be analyzed both by measures of central tendency as well as variability (Bartz, 1971).
Sample mean computed from this data set is 5.421875. This reflects a high level of job satisfaction arising from extrinsic factors. On a scale of 1-7, the majority of those interviewed recorded their satisfaction level above the average figure thus resulting into a high mean score.
This can also be explained from the median and mode point of view. This data set has a median and mode of 5.6. Median is the central figure that separates the two halves, i.e the lowest-value side and the highest-value side, in a frequency distribution (Bartz, 1971). A median of 5.6 represents a positively skewed data since it is higher than the mean.
The mode which describes frequency distribution also falls at 5.6, clearly indicating that the majority of those interviewed recorded their level of satisfaction at 5.6 slightly higher than the mean score hence a positively skewed data. Figure 2.1 depicts a visual illustration of this information.

Figure 2.1: Job satisfaction by Extrinsic factors
Source: Researcher.
Apart from the central measures of tendency, measures of variance can also provide an insight into this data. Both the standard deviation and variance are measures of trend characterizing the dispersion among various measures in a population. They show how tightly all the values are clustered around the mean in a data set ((Bartz, 1971). They express the inconsistency of the population by showing how far away from the mean the data points tend to be (Bartz, 1971).
A small value, of both, reflects a distribution in which most data points tend to be close to the mean as evidenced in this data set. This data set has a variance of 0.232732 and a standard deviation of 0.482423. In addition, standard deviation is a measure of confidence levels in empirical conclusions. An acceptable empirical error margin is at two standards deviations from the mean resulting into 95% confidence level.
This data set is normally distributed since 68% of the values are within one standard deviation from the mean ranging between 4.9 and 5.9 and 95% of the readings fall within two standard deviations ranging between 4.5 and 6.4. This information is visually portrayed in figure 2.1. If the bars were to be joined by a line, then a bell shaped diagram would result.
The significance of charts/graphs in conveying information
Charts and graphs help readers to have a better understanding of the meaning of data. They convey information in a manner that can be easily understood (Bartz, 1971). Besides, through the use of graphs and charts, differences between separate pieces of data can be clearly illustrated in a clear method.
Lessons learnt from the results
The importance of descriptive statistics as a first step in data analysis comes out clearly in this study. Although the results reveal very little concerning the subject of study, much is learnt about the frequency distribution and the nature of population dispersion thus forms a benchmark against which other detailed data analysis can be done.
The results from this study can lead to the conclusion that both position and extrinsic factors play a key role in influencing employees’ job satisfaction.
Reference
Bartz, A. E. (1971). Basic descriptive statistics for education and the behavioral sciences (4th ed.). Oxford, UK: Burgess.