What are collinearity and multicollinearity?
The phenomenon that appears when in a multiple regression two predictor variables have a non-zero correlation is known as collinearity; at the same time, the effect when more than two variables are correlated with one another is recognized as multicollinearity. The latter phenomenon does not tend to influence the statistic variables such as p values, F and R2 ratios, and also does not affect the regression model generally. Overall, multicollinearity should not produce an effect on the predictions that are made by the regression model. However, when one is interested on the individual predictors and their effects, multicollinearity is likely to represent a significant challenge.
How common is collinearity or multicollinearity?
Multicollinearity or collinearity can be found in the vast majority of quasi-experimental and non-experimental studies when observational data is collected. The only type of study unlikely to have these phenomena is a designed experiment. However, the major issue is not merely the presence or absence of collinearity or multicollinearity but the effect they produce on the data analysis. In other words, in practice it may not happen often that two variables are in a perfect linear correlation, but in economic estimations it is often the case that multiple variables are in a strong correlation.
Causes for multicollinearity can also include:
- Insufficient data. The this is the problem, it is possible to address it by means of collecting more data.
- Incorrect use of dummy variables. For instance, due to a researcher’s error one of the redundant categories my end up included; or the dummy variables may be added to some of the categories.
- Combining two variables that are supposed to be separate. For instance, a researcher could use the variable of total investment income that is actually a combination of income from savings interest and income from stocks and bonds.
- Using two variables that are identical. For instance, one could by mistake include bond income and investment income and savings as two separate variables.
Types of multicollinearity
Is it possible to distinguish between two primary types of multicollinearity:
- Structural multicollinearity – a mathematical artifact caused by the use of the existing predictors to generate new ones (for example, creating the predictor y2 from the predictor y).
- Data-based multicollinearity – a result of an experiment with a flawed design or basing the analysis on the observational data only.
Level of collinearity or multicollinearity
Imperfect multicollinearity can be of high and low levels. In particular, it occurs when the variables used in an equation are correlated in an imperfect manner. Differently put, this phenomenon can be presented as: X3=X2+v, (knowing that v represents a variable that is random and can be seen as an ‘error’ in the exact linear correlation).
Low level: Under the low level of correlation between X’s, β can be estimated confidently because OLS provides a wide range of information for that.
High level: Under the high level of correlation between X’s, the amount of information available to OLS is very limited and it complicates one’s capability to distinguishing the effects on Y produced by X1 and X2. In that way, β can be estimated with a high level of uncertainty.
Consequences of Imperfect Multicollinearity
When multicollinearity is imperfect, the estimators of OLS can be acquired; besides, they can be categories as Best Linear Unbiased Estimators or BLUE. Regardless of the fact that linear unbiased estimators possess minimal variance, those of OLS are usually larger than the variances that were found without the impact of multicollinearity.
Concluding when imperfect multicollinearity is present we have:
- Estimates of the OLS may be imprecise because of large standard errors.
- Affected coefficients may fail to attain statistical significance due to low t-stats.
- Sing reversal might exist.
- Addition or deletion of few observations may result in substantial changes in the estimated coefficients.
Perfect Multicollinearity
When the linear relationship is perfect, it is possible to use an example of the model below:
Y=β1+β2X2+ β3X3+e
where the sample values for X2 and X3 are:
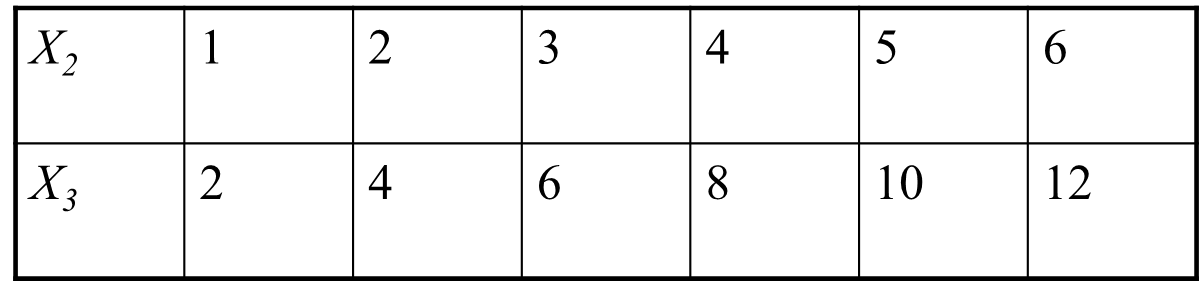
It is seen that X3=2X2. In turn, it may seem that the quantity of the explanatory variables is two, in reality is it just one. The explanation is simple –this is the case due to the collinearity of X2 and X3 or because X3 is the precise linear function of X2.
Consequences of Perfect Multicollinearity
When multicollinearity is perfect, the estimators of OLS are nonexistent. An attempt to estimate an equation with a perfect multicollinearity of specification in Eviews will fail. In response to such attempt Eviews will show an error.
The Detection of Multicollinearity
Two regressor model
High Correlation Coefficients
Among independent variable, pairwise correlations may have high absolute value. In cases where the correlation is > 0.8 there is a chance that severe multicollinearity takes place.
More‐than‐2 regressor model
High R2 with low t-Statistic Values
It may be possible for the general fit of an equation to remain high even though its individual regression coefficients are insignificant.
High Variance Inflation Factors (VIFs)
Variance Inflation factors estimate the increase in the variance of the measured coefficient due to the impact of multicollinearity. This relationship is reflected in the degree to which the explanatory variables in the equation are capable of explaining a single variable. There are tests that allow assessing multicollinearity; they are Farrar-Glauber test, Condition number test, and Perturbing the data.
Remedies for Multicollinearity
Do Nothing
At times, doing nothing is the best suitable course of actions. However, it is possible to inform that a number of predictors tend to jointly predict a certain result and it makes sense to collect more data to estimate their effects separately.
Drop a Redundant Variable
One more important aspect to pay attention to is the impact of unnecessary variables. If one of the variables is redundant, its presence in the equation can be characterized as a specification error. Such variables need to be detected and dropped according to the guidance in the economic theory.
Transform the Multicollinear Variables
In addition, it can be possible to minimize multicollinearity by means of re-specification of the model. One example of such reduction is via creating a combination of the multicollinear variables.
Increase the Sample Size
Moreover, the precision of an estimator can also be maximized when the sample size is increased. This measure also reduces the negative impact of multicollinearity. However, the addition of data may end up not being feasible.
Use other approaches
Ridge Regression and Principal Component Regression are the additional strategies helping to address multicollinearity.
Real life examples
Example One
One predictor variable in the model is found to be in a direct causal relationship with another predictor variable.
For instance, the model that includes the total gross income of a town as well as the size of its population is used to determine the contribution to the town’s charity funds. It is possible that the estimations will find that the two variables are in a high correlation since the town’s population size contributes directly to its total gross income. To address the issue, the model needs to be restructured avoiding the regression of two related variables (omitting one of the variables or combining them).
Example Two
A model includes two predictor variables that in turn represent a common latent variable construct (the halo effect)
For instance, several measures of customer satisfaction are used to assess customer loyalty and two of them (network satisfaction and product satisfaction) are in a high correlation because the customers’ description of satisfaction did not refer to these predictors separately. In this case – the two measures work as a reflection of a single predictor – the overall customer satisfaction. In that way, to avoid the problem, the latter common predictor could be used as a variable instead of two separate reflections.
References
P. Kennedy. A Guide to Economics. Cambridge MA: MIT Press, 2003.
D. Neeleman. “Some remarks on linear economic model,” in Multicollinearity in Linear Economic Models. New York, NY: Springer Science & Business Media, 2012, ch. 1, pp. 1-14.