Historical Context of Perspective Drawing
Perspective drawings entails portraying three dimensional spaces into two dimensional spaces, and are classified into aerial and linear perspective. Historically, perspective drawing was examined by philosophers including Euclid, Roger Bacon, and Robert Grosseteste according to their professions, and the way they made observations of the visible world.
Duccio and Giotto immensely contributed to the study of perspectives through paintings representing real world observations. The underlying goal was to accurately describe what a viewer was seeing with changing vision changed, leading to the mathematical theories of perspective drawing by Piero della Francesca in 1478. Albrecht Dürer (1471-1528) discovered drawing machines as illustrated in figure 1 below, where different positions of the same object are attained because of variations in viewing positions.
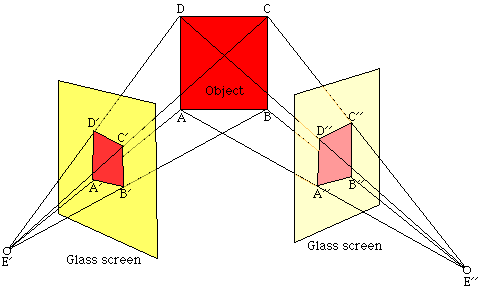
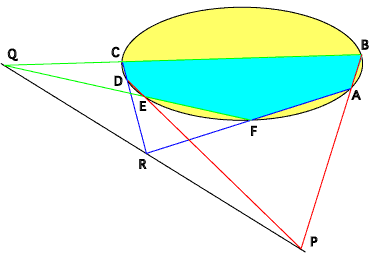
Other contributions were made by Leonardo da Vinci (1452-1519), where geometry and painting were combined, Albrecht Dürer (1471-1528) on the ‘practice of geometry’, Girard Desargues (1591-1661) on ‘projective geometry’ for slotting a point, x, for mapping points to points and lines to lines, as shown in figure 2 below, the advent and propagation of the use of mathematics in perspective drawing.
Math Used In Perspective Drawing
The mathematics used in perspective drawing includes a one point, two point, and three point perspective.
One point perspective
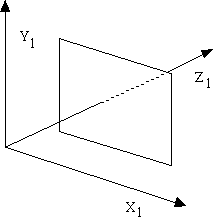
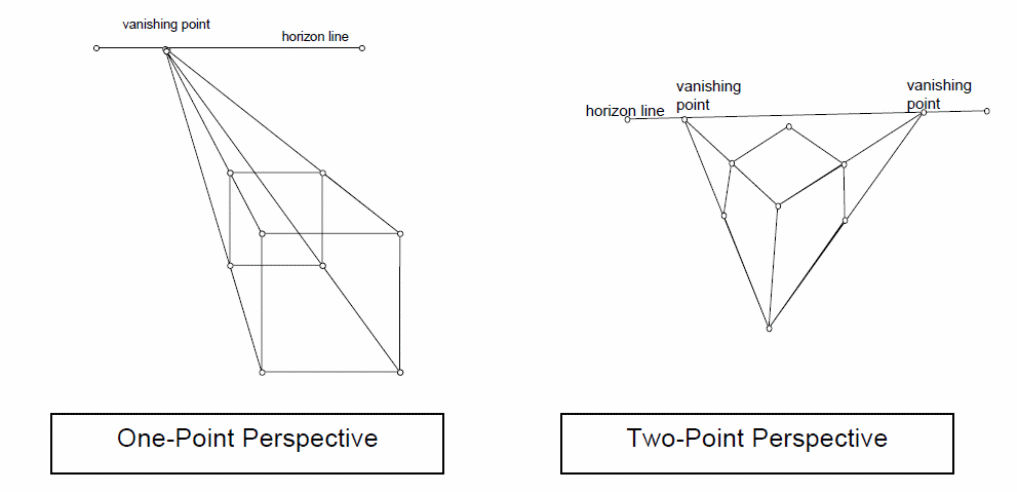
One point perspective is defined by diminishing points as the distance from the observer increases. Take a specific point of choice as the center point and eye point of an object with the axes of the objects having parallel orientations to the drawing plane as an example. If the center point is cp= [6.0, 5.0, 2.0], and the eye point is ep= [6.0,-15.0, 2.0], and the y=l plane is parallel to the x and y axes, there is no rotation because dp= [0, 20, 0]. In this case, the position of the center point is the vanishing point. Figure 2 illustrates one point perspective with one point projection axes. The projection plane is pierced only by one principal axis (Z1).
Two point perspective
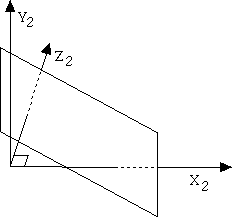
The projection plane is pierced by two principal axes in a two point perspective as shown in figure 4 below. If the eye point is ep= [16.0,-15.0, 2.0], and the center point is cp= [6.0, 5.0, 2.0], such that there is a rotation about the z axis, by taking dp= [-10, 20, 0], then, for y=l and z-axis are parallel. The y2 axis does not pierce the axis. Axes or points can rotate in this system.
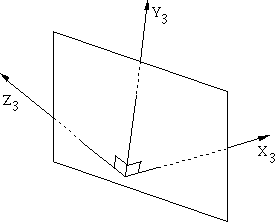
Three point perspective
The three point perspective occurs when the line of projection is pierced by three principal axes. As illustrated in figure 5 below, the projection plane is pierced by the X3, Y3, and Z3 axes.
How perspective drawing involves the mathematical ideas
Mathematical ideas are involved in perspective drawing because it lies on the rations of the objects that are drawn as illustrated in figure 6 below.
Bibliography
Barsky, Brian A. A Note on the Mathematics of Two- and Three- Point Perspective. Web.
Boyer, Carl B., A history of mathematics, Princeton University Press, Princeton, 1985.
Treibergs, Andrejs, The Geometry of Perspective Drawing on the Computer. Web.