Introduction
The report involves an experiment to collect data from the collision of objects to develop a mathematical and graphical model that can be compared to the Impulse-Momentum Theorem. In the experiment, there is a moving cart to which a force is applied and a stationary cart, each weighing 25.4g and set to collide on a track. During each collision trial, the force readings from force sensors, the time taken by the moving cart, and the velocity of the stationary cart after collision are recorded. Impulse for each trial is then calculated using the formula J=F∆t, and a graph of velocity against time is plotted.
The experiment shows a relationship between the velocity of the stationary cart and the impulse applied to it after the collision. Additionally, the results and calculations for the experiment show similarities to the equation with the impulse-momentum change equation that states Force (F) x Time (t)=Mass(m) x change in velocity (∆v).
Data
Both the cart on track and the stationary cart are set to weigh 252.4g each.
Results
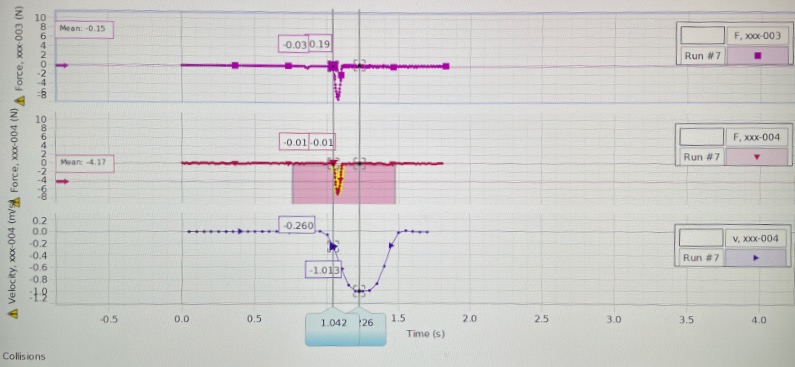
Figure 1: Results for Force, Velocity, and Time as recorded from trials
Calculations & Graphs
Impulse (J) is calculated using the equation J = F∆t.
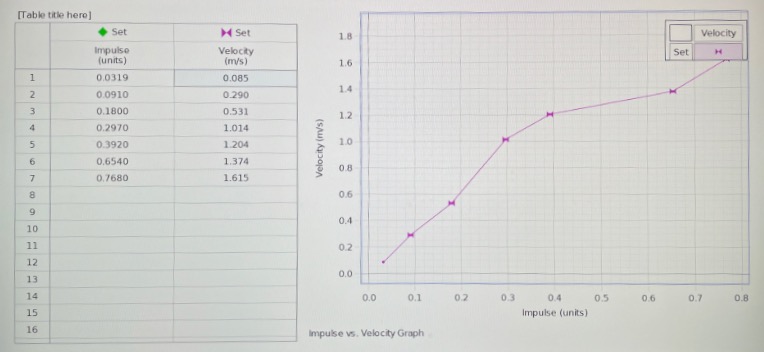
Figure 2: Calculations for impulse from the trial experiment
Discussion
The slope of the velocity-impulse graph relates to a property that states mass is always constant. The y-intercept is the velocity of the collision. The y-intercept has a positive value because the action force applied by the moving cart is greater than the reaction force of the stationary cart.
Therefore, the velocity during collision impact will only be reduced. The results are consistent with the Impulse-Momentum Theorem. Since the masses of the objects are constant, the calculation of impulse and the positive curve shown in the velocity-impulse graph shows that the curve satisfies the impulse-momentum change equation.
Some of the factors that affect the motion of a stationary cart include friction between the stationary cart and the surface, velocity of the moving cart, elasticity of the moving cart, and mass of the moving cart. Factors over which one has little or no control include the friction between the stationary cart and the surface and the accuracy of the devices. The factors that directly relate to each other are the mass and velocity of the moving cart. By setting impulse as an independent variable, the dependent variables include collision force and elasticity of the moving cart.
The changes to impulse applied to a stationary cart are predicted to increase the cart’s velocity by some degree, depending on various factors such as force applied, that is, Impulse (J) α Velocity (v) (Naskar, 2018). Higher impulse will result in a higher velocity of the cart’s movement. Similarly, a lower impulse has a lower velocity effect on the cart.
Conclusion
The report results and calculations show a relationship between impulse and velocity through the impulse-momentum change equation. Furthermore, the Impulse-Momentum Theorem is similar. Therefore, the report shows that a successful model to experiment with the effect of collision has been developed.
References
Naskar, A. (2018). Impulse and Momentum – Thoughful Physics. Quantemporary.