Calculus-Integration Essay

Indefinite integrals

The most important characteristic of calculus is the relationship between the concepts of derivative and integral. The relationship is summarized by simply saying that integration is the opposite of differentiation. The relationship is synonymous with subtraction and addition which we know serves to undo each other or division and multiplication which work on the reverse principle.

Essentially, differentiation is a process that is developed from an original function say f, and the new function or the derivative is f’. The previous discussion calls us to ask ourselves that if we are given the derivative function f’, will it be possible to find the original function?

As noted, indefinite integration is simply the opposite of differentiation and is sometimes referred to as anti-differentiation (Dadkhah, 2010). If an indefinite integral function is F and given a certain function f, the function F or the integral is determined such that F’ equals the original function f (Dadkhah, 2010). Indefinite integration is essential in calculus.

It is a technique used to find the distance traveled by projectiles, electrical and physical equations or the area under a curve. For instance, the equation of instantaneous current through a capacitor is i =CdV/dT where I is the instantaneous current; t is time; V is voltage and C is the capacitance. The unknown voltage can be determined through integrating the function at time t.

Going back to the question, F is the anti-derivative of f on a certain interval l if F’(x) = f(x). F is also known as an anti-differential of f(x) dx on l. The process of obtaining anti-derivatives is what we call integration. The indefinite integral of f(x) on the interval l is a set of all integrals of f(x) on interval l and is denoted as

This means that it is a set of all functions of F whose values satisfy the equation F’(X) = f(x).

Example: Determine a function that can be differentiated to attain the function below.

F(x) = x³+ 4x – 6

Solution: We can begin by differentiating this function in order to have a clue on how to find the actual solution. The differentiated equation will be: F’(x) = 3x²+ 4. This step reminds us of how to find derivatives. To differentiate the powers of x, the rule is to multiply the expression by the power and reduce the power by one. Going back to the example, we can begin with the first expression x³.

The term x³ must have been attained by differentiating an equation and since we reduce the power by one, t it seems that the differentiated term was x⁴. But the derivative of x⁴ would have been 4 x³ and there is no 4 in our first term. Therefore, this 4 must cancel out to have the correct derivative. It seems that (¼) x⁴ must be differentiated so as to attain x³.

Similarly, the expression 4x would be attained if we differentiate (4/2) x². Two (2) at the denominator is for canceling the 2 we pick from the power during differentiation. The final expression is a constant and it is clear that the derivative of x is 1. Hence, it also applies that the derivative from which -6 came from was -6x.

Combining all the answers we get the equation F(x) = (¼) x⁴+ 2x²– 6x. We can confirm the answer by differentiating F’(x) = x³ + 4x – 6. Since the derivative of a constant is zero, any constant included in the function satisfies the integral (Dadkhah, 2010). Therefore, the function can take the form F(x) = (¼) x⁴+ 2x²– 6x + c. Where, ‘c’ is a constant.

Definite integral

Formal definition

Assume we are given a function f(x) at the interval [s, t] and told it is continuous at this interval (Dawkins, 2003). We can subdivide the section [s, t] into n very small sub-section with identical widths of Δx. For every subsection we select a point x_i as illustrated below.

Therefore, a definite integral for f(x) in between s and t is obtained by:

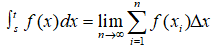
where dx mean the integration is done with respect to x.

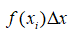
denotes the area (length * width) of each subsection (Dawkins, 2003).

Explanation

The notation

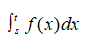
is used to denote a definite integral of a function f(x) integrated with respect to x. In order for us to understand it, we equate it to a simpler equivalent that we are more conversant with like

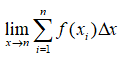
We can break this function in to smaller sections to easily comprehend it. However, before that, we explain our earlier subdivision of the intervals. A curve can be said to be a series of equal minute lines of width X joined in varying angles to bring the effect of an arc. These arcs when joined together form the curve f(x). These minute lines form rectangles whose area is

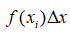
when bound by two values of

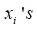
on the side and the x-axis on the lower end. By summing the areas of these small rectangles, we form

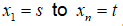
Thus, we obtain the area bounded by the curve f(x) and the x -axis in the interval [s, t]. This is denoted by

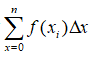
Under normal circumstances, this would be sufficient. Nevertheless, since we are dealing with a curve, all the above is only possible if it is continuous. As earlier noted, for any function to be continuous its limit must exist. We therefore introduce the limit in our earlier function in order for it to hold true for all curves. It thus becomes,

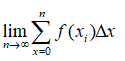
Theoretically, the definite integral of any function f(x) for any given interval is the area bounded by the x-axis and the function itself between the interval values. For this to be evaluated, the function must be continuous (Dawkins, 2003).

Example

Since we will have to evaluate the limit, we have to simplify the summation using some formulas. Note that i is a variable and n a constant and therefore the summation can be broken as below:

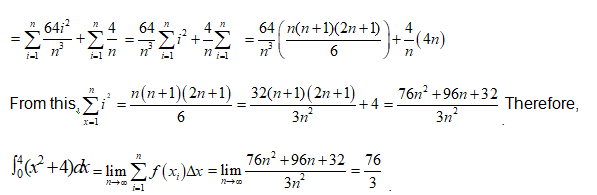
In advanced calculus, there are several ways of evaluating the definite integral without using the definition as above. Irrespective of the method used, the answer should always be the same.

References

Dadkhah, K. (2010). Foundations of Mathematical and Computational Economics. New York, NY: Springer.

Dawkins, P. (2003). Paul’s online math notes. Retrieved from: http://tutorial.math.lamar.edu/Classes/CalcI/DefnOfDefiniteIntegral.aspx