Decision Theory
Decision making
Chapter three Decision Theory is a discussion on how software designers and IT security professionals can make good decisions using the decision-making theory when faced with different alternatives. The following objectives were sued to make good decisions.
Objectives
- To understand the meaning of a decision
- To investigate the steps necessary to make a good decision
- To formalize the decision-making process
A decision is defined as the conclusion that is made when different alternative solutions are compared and the best one chosen. The utility of a solution (U) is very important in determining whether a decision is good or bad. When making a decision, different candidate solutions exist, and each has its own utility. However, the utility of the solution depends on the outcome of the solution when an action is applied to produce an outcome.
A good decision has a higher utility and a higher probability of producing better results than a bad decision. If the utility of a decision is EU (a) is put on the left side of an equation, the right side of the formula will indicate the formula for calculating the utility function. Here, the utility is calculated by integrating the right side of the equation function, which is the product of the utility (U) and the probability of occurrence, P.
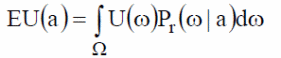
Techniques and methods
Different tools such as the Thompson’s tree, the Laplace method, and the expected value of return can be used to calculate the utility of a decision. For instance, using Bayes’ theorem, IT security specialist can make a good decision from either to apply a countermeasure or not to protect data. Let ‘A’ represent the probability of investing in the countermeasure, and ‘B’ represents the positive outcome after a countermeasure has been implemented.
P=the probability of a good return on investment
1-P=the probability of a negative return on investment
Let P (FO=favorable outcome) and P (UF=unfavorable outcome)
Assume that P (FO) =0.87 and 1-P (UF) =0.13, then, the probabilities can be revised according to Bayes’ theorem to provide accurate results where P (accurate revised probability) is given by:
If the countermeasure were not used, then p (negative) =1-0.539=0.461, showing that the decision to use a countermeasure is better because the utility is p=0.539.
Results and conclusion
The results show that decision making is a process that depends on what the decision-maker understands the meaning and how the decision-maker uses the tools and techniques available to make good decisions.
According to the results, the decision to use a countermeasure is high p=0.539, which is above the utility gained if a decision was made not to use a countermeasure to protect data in an information system. In conclusion, the paper strongly recommends the use of effective decision-making tools and techniques to avoid the adverse effects of poor decisions.
Forecasting Techniques
Forecasting
The paper provides a detailed discussion of the importance of using forecasting techniques and modelling tools to efficiently allocate resources that meet the needs of tourists visiting a city. Resources can be allocated using econometric models to predict the demand for services or time series methods to predict how best to allocate available resources. The author compared the ARMAX, ARMA, and ADL, TVP, and VAR econometric models by evaluating the findings to arrive at an informed conclusion, based on the following objectives.
Objectives
- To compare the value of search data using ARMAX with ARMA models
- To determine the most accurate econometric models among the three models to use in tourism forecasting.
The techniques and Tools
One of the tools used in the study was the Google search engine that was queried to generate search data for almost two years. The parameters used in the study were estimated for 60 weeks, and the parameters used to validate the results were estimated for 21 weeks. Here, tourism demand is ‘yt‘ and the number of weeks is t, and the search queries were represented by x3t and x5t. The demand for tourism is ‘yt’ at the time t, and the error Q occurs at time t. The family of models that were used to evaluate the performance of the Google search engine includes AR, ARMA, and ARIMA.
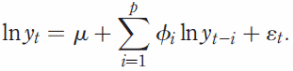
By making p=1, two different results were obtained in the model estimation calculations using the time series and the unit square root test. The results show that the demand for hotel tourism is not constant or stationary despite some variables being stationary.
Results and Conclusion
Many of the traditional methods that are used to forecast tourism demand do not provide accurate results because the accuracy of a model does not increase with its complexity. For instance, when p was assigned values (p=1, 2), the results of the econometric models using ARX (1), ARMAX (1, 1), ARIMAX (2, 1, 2), ADL, TVP, VAR, ADL, TVP, and VAR respectively, the results were not in favor of the were econometric models.
Computations, based on the mean absolute percentage error (MAPE) and the root mean percentage error (RMPE), showed that ARX1 yielded 6.896 against RMSPE and 5.529 for MAPE. However, assigning p values for ARMAX (1, 1) based on RMPSE and MAPE, the results were 7.021 and 5.565, and for ARIMAX (2, 1, 2) respectively.
The respective values were 9.783 and 7.918. ADL TVP and VAR were 9.766, 8.238, and 9.773. However, when the models were computed against RMSPE and MAPE, the results were 8.339, 9.019 and 7.874 respectively. In conclusion, using the ARMAX models to forecast provided better results than using the ARMA forecasting models.