Introduction
The experiment was conducted to estimate the acceleration due to gravity based on the kinematics equation of motion in three scenarios: a fan-powered cart, cart motion along an inclined plane, and a free-falling ball. The relationships between velocity and time and position and time were used to assess whether the experiment results agreed with the theory of motion and gravity. When the equations generated from the graphs matched the theoretical equations, the researcher proceeded to calculate acceleration due to gravity. The researcher realized an error of 51%. From the graphs, it was deduced that the report results were consistent with the laws of motion.
Data Analysis
A Cart on a Track
The observed measurements and final results did not have a clear pattern. Furthermore, there was no clear trend in the graph. The plots were random values – they could not be predicted. The tables below indicate the data results from the various experiments.
- Initial Position, x0 = 2.0 m
- Final Position, x = 0.3 m
- Distance, Δx = 2.0 – 0.3 = 1.7 m
Table 1a. Time Taken by a Fan-Powered Cart to Travel the Specified Distance
Average of Trials = (4.12+4.25+4.59+4.57+4.75+4.75)/6 = 4.505 s
Cart Acceleration, a = 2 Δx/t2 = 2(1.7)/4.5052 = 0.168 m/s2
Table 1b. Velocity vs. Time Graph.
A Cart Down the Incline
Average of Accelerations from Distance and Velocity Graphs = (0.0896+0.0884)/2 = 0.089 m/s2
- Initial Position, x0 = 2.0 m
- Final Position, x = 0.3 m
- Distance Traveled, Δx = 1.7 m
Table 2a. Time Taken by a Cart to Travel the Specified Distance Along an Inclined Plane
Average of Trials = (2.56+2.5+2.43+2.53+2.56+2.5)/6 = 2.51 s
Cart Acceleration, a = 2 Δx/t2 = 2(1.7)/2.512 = 0.54 m/s2
Table 2b. Velocity vs. Time Graph
Average of Accelerations from Distance and Velocity Graphs = (0.414+0.443)/2 = 0.429 m/s2
Incline Angle, θ = sin-1(h/H) = sin-1(0.13m/2.11m) = 3.53°
Acceleration due to Gravity, g = a/sinθ = 6.97 m/s2
A Free Fall Ball
Table 3a. Time Taken by a Ball to Fall the Specified Distance
Average of Trials = (0.35+0.65+0.34+0.37+0.47+0.62)/6 = 0.47 s
Acceleration, a = 11.6 m/s2
Table 3b. Velocity vs. Time Graph
Average of accelerations from position vs. velocity graphs = -14.8 m/s2
Acceleration due to gravity, g = -9.81 m/s2
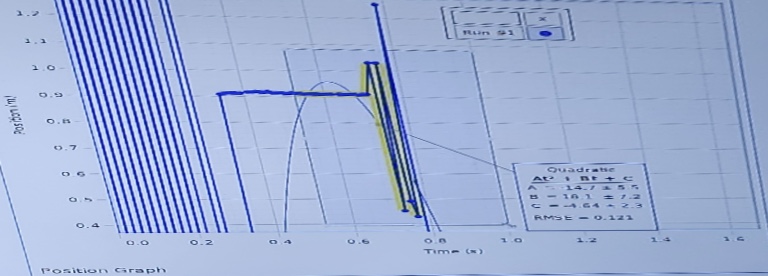
The calculations showed that acceleration (a) and coefficient (A) relate such that 2A=a. Additionally, the quadratic equation of the curve obtained, x = x0+vit+½at2, was similar to y=ax2=bx+c. From the graphs of velocity against time, the results estimated that the velocity of an object in motion decreased with increased time.
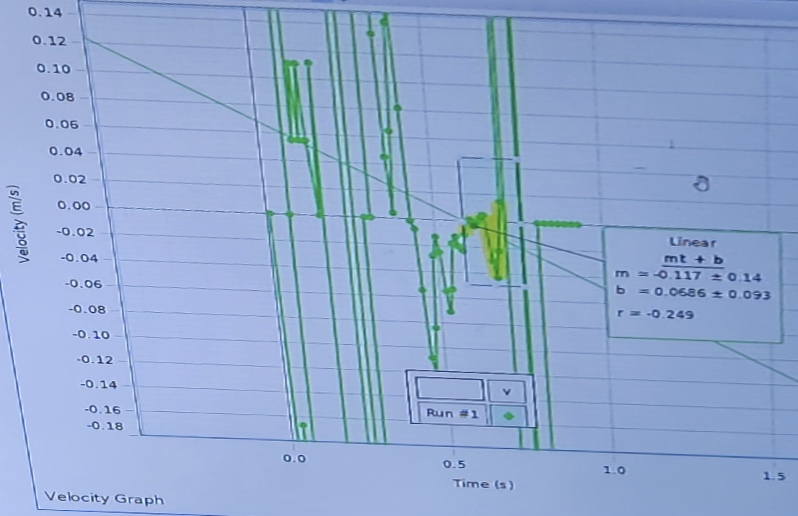
However, the graph of position against time showed that as time increased, the position increased to a given level, and then it started to fall. It was concluded that the experiment satisfied the kinematic equations of motion since the equations generated from the graphs matched the theoretical equations.
The deviations in data results were due to the uncertainty inherent in the experimental method. From the initial measurements, there existed elements of randomness in recording the stopwatch timer and position reading by the motion sensor. The experimental uncertainty is solved by conducting as many trials as possible using an accurate device and working within a regulated environment due to its nature (Kumar, 2020). For example, the table below shows that the errors calculated from stopwatch readings for the inclined plane experiment are random – they have no pattern.
Conclusion
The researcher realized that the experimental results matched closely with the theoretical expectations. The report showed that the errors could have resulted from the limitation of experiment data, inaccuracy of the tools, and increasing data sample size by conducting as many trials as possible. Similarly, the researcher found that using more accurate sensors could improve the reliability of collected data.
Reference
Kumar, S. (2020). Newton’s Laws of Motion and Friction Mechanics (Vol. 3). Sanjay Kumar.