One of the fundamental features of mathematics is that it can be applied to real objects. This justifies the origin of this science as primarily a craft for measuring, evaluating, and shaping natural objects not on paper but in life (Wittmann, 2021). This presentation will discuss how geometric concepts find applications in life. In particular, I will focus on the use of Pythagoras’ theorem. The idea behind this theorem is that in right triangles, the square of the hypotenuse is equal to the sum of the squares of the catheters (Africk, 2021). This seemingly uncomplicated equation makes finding either side in right triangles possible when the other two are known. Crucially, the triangle to be studied must be right-angled, meaning that one of its angles is 90° and the other two combine to give 90°. For this project, I will choose one of Apple’s latest innovations, the 12.9-inch iPad Pro, as the actual object to measure (Apple, 2022). This will support the relevance of the study.
I did not use measurements on the actual iPad Pro but instead literally put a ruler against the computer screen to measure the sides of the iPad Pro screen. In other words, the measured values were not the actual dimensions but instead were the lengths of the three sides measured to some scale. The lengths I found with the ruler I recorded on the slide. You can see the upward trend perfectly: 9.5 cm, 12.5 cm, and 15.7 cm.
In the previous step, Pythagoras’ theorem was not used because all the sides (or rather their projections at some scale) could easily be detected with a real plastic ruler. However, Pythagoras’ theorem is used here to check the literacy of length measurements and to determine whether there are cases in which Pythagoras’ theorem turns out to be infeasible. So, in order to implement this theorem, we need to refer to the formula:
Suppose we do not know the length of the hypotenuse c, but we have two measurements of the catheters, a and b. Let us substitute the obtained values, and we realize that
All that is left to do is to take the root of this number and determine the calculated hypothesis length value:
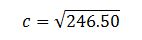
Notably, by the rules of mathematics, both answers, negative and positive, are the roots of this equation, but since I am talking about geometric parameters, using negative length is unacceptable. In other words, the length of the hypotenuse calculated with a ruler is 15.7 cm.
Hence, all measurements and calculations have been done so that we can proceed to conclusions. First, it should be said that Pythagoras’ theorem turns out to be a valuable tool wherever there is a right angle — it allows you to calculate the lengths of any of the missing sides when there are two others: the two cathetuses or the cathetuses and the hypotenuse. The hypotenuse measured with the ruler was exactly 15.7 cm; precisely, the same value was obtained by calculating the Pythagoras formula. It means that the measured and calculated values turned out to be absolutely identical. Their equality is due to the iPad Pro screen’s even, geometrically correct sides. Both sides intersect strictly at 90°, which creates perfect conditions for applying Pythagoras’ theorem without errors. It must be said that the iPad Pro picture has rounded edges, which at first glance creates an obstacle for the strictly perpendicular sides of the screen. However, it is worth understanding that the rounding has no effect on the real angle, which is formed by the imaginary extension of the sides to their intersection at 90°. If the calculations did not turn out to be identical measurements, then among the reasons would be the error of the ruler, the inaccuracy of measurement, taking into account even fractions of a centimeter, or the lack of a real right angle.
This project taught me how to look for mathematical concepts in real life. Now, when I look at ideal shapes, I automatically build measurements for them and try to identify missing dimensions — an excellent analytical skill. In addition, I have learned to look for reasons for different totals from the project as I began to think about why the hypotenuse might be unequal even before the calculations. This contributes to my critical thinking as a researcher.
References
Africk, H. (2021, September 05). Pythagorean theorem. LibreTexts. Web.
Apple. (2022). iPad Pro 12.9‑inch. Apple, Inc. Web.
Wittmann, E. C. (2021). Connecting mathematics and mathematics education. Springer.