Introduction
Depending on what reactions are induced in an object in response to an applied force, it can be regarded as a point particle or an extended object. In the first case, the force affects the particle so that it causes it to move in space, but does not cause it to rotate. In the case of an extended object, the force also causes the object to rotate around its axis.
It is noteworthy that the nature of the rotation of such an object depends on the point of application of the external force, which is realized through the formation of torque on a thin rod. The torque on a thin rod has a direction that leads to a shift in the equilibrium of the suspended object, and the direction of the torque turns out to be perpendicular to both the force vector and the direction vector of the rod itself (SS, 2022). In the present work, different forces are applied at different distances to a thin rod
Data
The primary data from the experiment performed are shown in Table 1 for ease of use in the statistical analysis. Table 2 shows the three additional measurements used to extend the current model.
Table 1. Original primary force and distance data for the experiment
Table 2. Extended analysis model for the experiment
Procedure
Figure 1 shows the experimental setup used to perform the current study. Forces of different values were applied to a thin rod suspended horizontally at different distances from the origin until equilibrium was reached, and all the distances and force values were measured (Table 1).
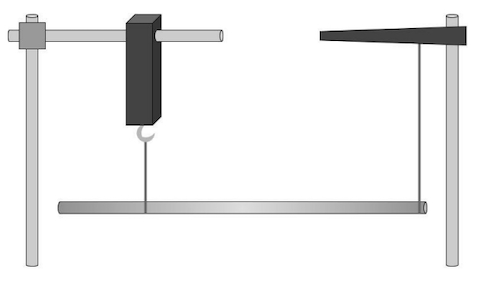
Results
Calculation
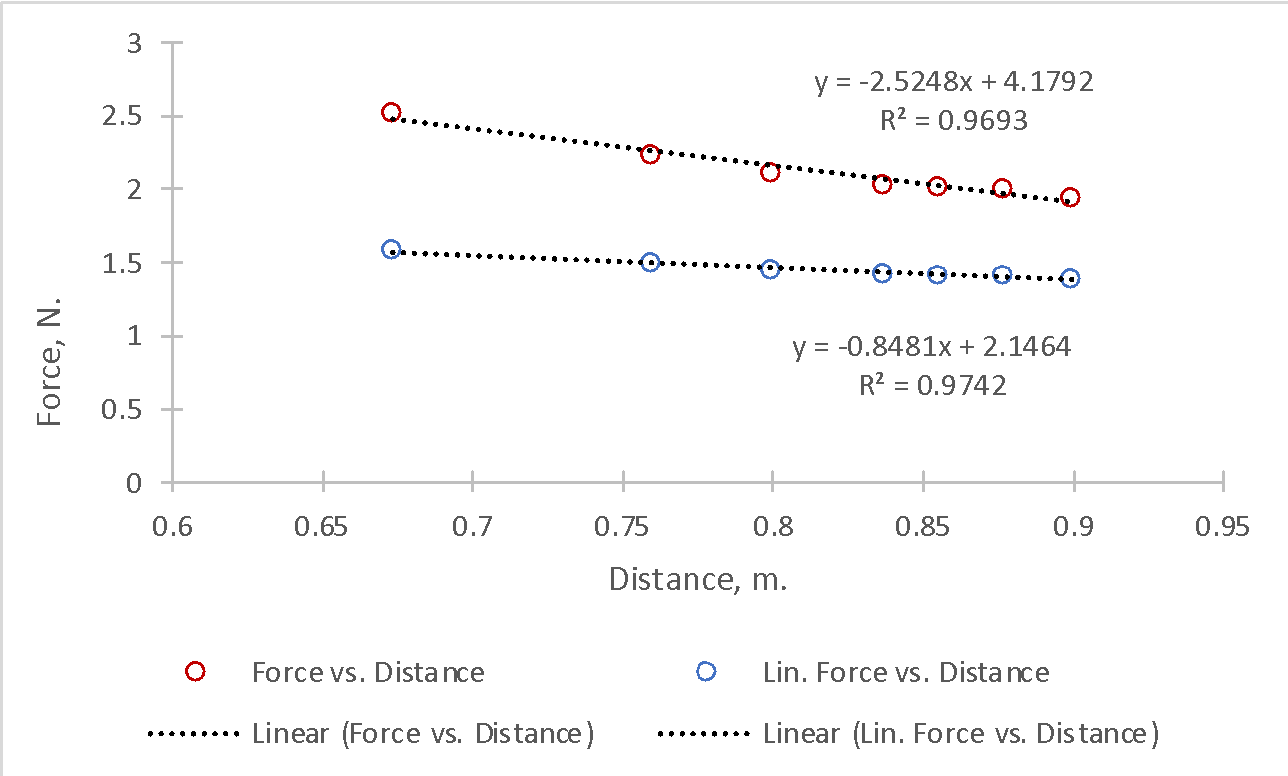
All data were collected in Table 1; no additional calculations were required for the current laboratory experiment. However, the calculations helped extend the model: in particular, using the resulting regression equations (Fig. 2), the predicted necessary force values were determined:

And for the linearized model:

The empirical values of the applied force for 0.596, 0.614, and 0.651 meters from the origin were 2.99, 2.77, and 2.65 N, respectively. It follows that the non-linearized model more closely matched the empirical values, and the percentage errors were:
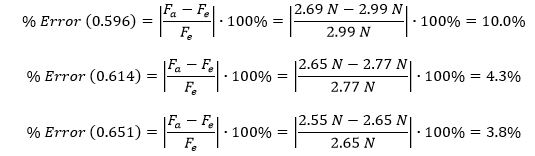
Graph
For the original data shown in Table 1, the force-distance relationship was plotted as shown in Figure 2. Overall, it can be seen that the dependence is well described by a descending linear function, and the coefficient of determination reports that the model covers up to 96.93% of the variance of the data set. Linearizing the power (taking the square root) increased the variance coverage to 97.42%.
In both dependencies, it can be seen that as the distance from the starting point increased, the values of the applied force before the thin rod reached equilibrium increased. In both cases, the slopes were negative (-2.52 and -0.85), corresponding to the rate at which the force decreased as the distance from the origin point increased.
At the same time, the y-intercepts made physical sense because they showed a nonzero value of the force applied at zero distance for a thin rod. In other words, they showed what force was applied to the rotation axis to achieve the rod’s equilibrium. If a metal rod were replaced by a wood rod with less mass, this would affect the moment of inertia as it relates to mass (SS, 2022). In particular, the moment of inertia for a wood-thin rod would be lower.
Conclusion
The present laboratory work aimed to investigate the dependence of the applied force on the distance to achieve equilibrium in the case of a horizontally suspended thin metal rod in light of the torque. The results showed that more force was required to achieve equilibrium as the distance increased. A downward linear trend was confirmed between the variables. This is consistent with theoretical expectations because for the torque of a thin rod, the formula τ = F×r×sin(θ) demonstrates an inverse relationship between F and r.
Reference
SS. (2022). Force and torque. Study Smarter. Web.