Summary
This lab work explores the use of vector rules to find the equilibrium state between three force vectors adjusted with a Force Table and a tunable force sensor. Two of the three pulleys on the Force Table were fixed with 100 g weights (at the 0° position) and 200 g weights (at the 90° position); the third pulley was fixed on a force sensor that was adjustable during the laboratory work. The equilibrium state of the three forces was determined by placing the ring connected to the three pulleys at the center of the Force Table. Table 1 contains information about each measurement and reports the uncertainties of these measurements. For mass, it was assumed that the minimum measured value was 1 g, so the uncertainty, in this case, is calculated as half of this minimum (±0.5 g). The same assumptions were made for the pulleys position since the minimum measurement was 1° (±0.5°).
Table 1: Results of direct measurements obtained empirically
Analysis
The data obtained were used to plot free-body and vector sums on cell paper, as shown in Figure 1. A ruler and transport were used for the construction, assuming that the size of one cell is 25 g.
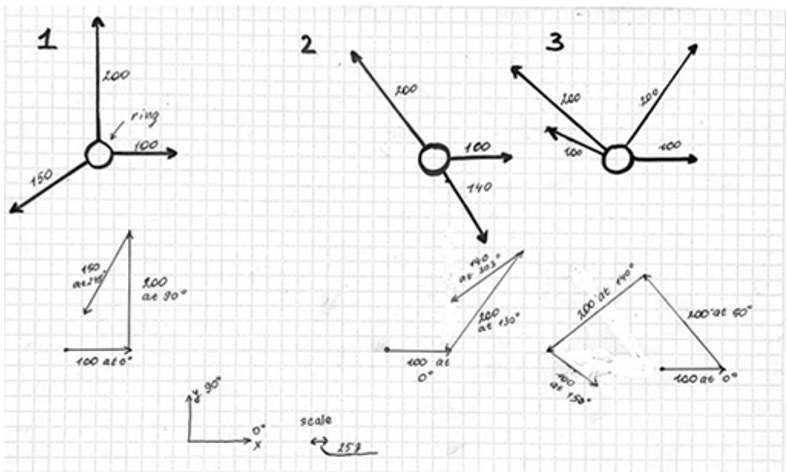
Each vector in the set can be written in the form of coordinate pairs. Each vector must be broken into two components by projecting the vector onto the X-axis and the Y-axis. In this case, for the first set, the three corrected vectors will be defined as (100, 0), (0, 200), (-75, -140). For the second set, the three projected vectors should be (100, 0), (125, 150), and (-125, -85). Finally, the third set with four vectors has the following values: (100, 0), (-125, 150), (-160, -125), (85, -50). Then it becomes possible to determine the vector sum that physically denotes the value of the resultant force vector, the very force that results from the superposition and is responsible for the equilibrium of the ring on the Force Table (Black, 2020). To calculate the three vector sums, the coordinates responsible for the X and Y coordinates must be added together in pairs:
- Force1 = (100+0-75), (0+200-140) = (25, 60)
- Force2 = (100+125-125), (0+150-85) = (100, 65)
- Force3 = (100-125-160+85), (0+150-125-50) = (-100, -25)
Thus, the vectors of each of the resultant forces were obtained by coordinate addition. According to the tutorial assignment, it was expected that the sum of forces for vectors should be equal to zero — only in this case, an equilibrium condition for the system, the so-called zero force, is reached. However, calculations showed that the vector sums were not equal to zero, which means that true equilibrium was not reached for all systems. The reasons for this may be, for example, errors in performing the experiment. In the case of uncertainties, the equilibrium may also be shifted due to measurement errors, but if it had been reached, one could postulate that equilibrium is reached under uncertainties.
Reference
Black, T. C. (2020) Physics 201 Lab 4: Static equilibrium and the superposition of forces [PDF document].