Functional mathematics allows you to trace the relationship between variables and predicts the value of a dependent variable from some independent factor through function analysis. The relationship between them can be anything: linear, exponential, polynomial, and other kinds of relationship, depending on the equation constructed. Some equation is always precisely defined for functions, which allows using any reasonable values of X to determine their influence on the parameter Y. The converse is true since any equation can be transformed to find X when Y is known. In this example, I have chosen to focus on the mathematical function of compound interest, allowing for profitable increases in capitalization through compounding. The basic compound interest equation is defined as follows:
As you can see, there are five variables in the function. A is a dependent factor that determines the future value of the money initially invested, P, at an annual interest rate r, accruing at some period n, over time t (Fernando, 2022). In fact, the function A(P,r,n,t) depends on four variables at once, which complicates the analysis task. Therefore, I decided to make three of them constants in order to study the function in a more meaningful way:
In this unique function, $1000 was invested at some interest rate r, according to the compound interest formula, every two months for a year (six times in all) for ten years. The $1000 is expected to turn into a more significant amount after that time, but now it can be seen that the particular value of A will only be determined through the interest rate r according to some polynomial relationship. If I enter a value of 0.05 as r, then in ten years, the amount will turn into $1645, as shown in the equation below. In fact, the applied meaning of such an analysis might be to choose the best interest rate that will save money faster. For example, at a rate of 0.09 after ten years, the value of money would be $2443, while at a rate of 1%, it would be only $1105. Thus, it is possible to measure the value of A based on the interest rate parameter.
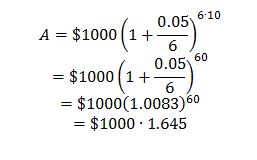
Reference
Fernando, J. (2022). Compound interest. Investopedia. Web.