Hamilton-Jacobi-Bellman Equations
The Hamilton-Jacobi-Bellman equation is considered a necessary condition in mathematics that describes extreme geometry in problem generalizations drawing from the calculus of variations. It is regarded as the best statistical method because it offers a sufficient and necessary condition for control optimality while remaining respectful of a loss of function (Maruta et al., 2020, p 159). In addition, the solution provides the value of the function, hence the equation is typically a nonlinear partial differential in the value function. The equation is calculated as follows:
− ∂J ∗ ∂t = min u(t)(L(x,u,t) +(∂J ∗ ∂x )f(x,u,t)).
With boundary condition J ∗ (ξ, T) = φ(ξ, T) for all ξ.
If x(T)is required to satisfy ψ(x(T), T) = 0, then the boundary condition becomes J ∗ (ξ, T) = φ(ξ, T) for all ξ that satisfy ψ(ξ, T) = 0.
Alternatively, J ∗ (x ∗ (t),t) = φ(x(T),T) +Z T t L(x ∗ ,u ∗ , τ)dτ.
Differentiate concerning t, obtain the HJB equation directly: dJ∗ dt = −L(x ∗ ,u ∗ ,t) = ∂J ∗ ∂t + ∂J ∗ ∂x ∗ f(x ∗ ,u ∗ ,t).
In this regard, in the context of the case study of Apple, the qualitative data can be adapted to the HJB equation by establishing a convergence and a quasi-optimal error estimate. The qualitative data can then be coupled with a quasi-variational inequalities system to give a monotone iterative scheme (Maruta et al., 2020, p. 160; Tedone & Palladino, 2021, p. 5662). As such, a consequence of iterated decisions will be generated, leading to the selection of optimal feedback control using the minimizer or maximizing through the so-called verification technique.
Linear Pearson Coefficient
Using a linear regression, the Pearson coefficient can determine the strength and direction of a correlation between two variables. The formula for the notion is as follows:
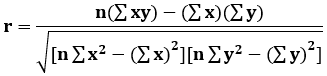
Where:
- r = Pearson Coefficient
- n= number of pairs of the stock
- ∑xy = sum of products of the paired stocks
- ∑x = sum of the x scores
- ∑y= sum of the y scores
- ∑x2 = sum of the squared x scores
- ∑y2 = sum of the squared y scores
In the context of business planning, as presented in the case of Apple, the formula can be adopted to assist in decision-making involving portfolio diversification. It is critical to assemble a portfolio based on risk and return parameters (Schober et al., 2018, p. 1765). This extends to the calculation of scatter plots across asset pairs such as small-cap equities, equities-bonds, debt-emerging market equities, bonds-real estate, and large-cap equities (Schober et al., 2018, p. 1766). However, it is critical to note that it remains limited in indicating causation for this case as it is mainly concerned with correlation.
Deterministic Control
The problem of deterministic control involves a stochastic disturbance of a unique type wherein, in particular situations, it arises that the state targets specific stochastic time points. As such, it ranges from continuous, stopping time, and impulse controls with limitations on optimal cost, including a viscosity solution with no disruption of the dynamics equation (El Farouq, 2017, p. 214). In solving the problem, the focus is on the disadvantage that arises from the cost optimization point of view utilizing a closed-loop feedback policy control rather than an open-loop one. In this regard, the deterministic problem is executed forward in time through its algorithm and then backward (Ahn et al., 2018, p. 65). These forward and backward algorithms perform the shortest graphical paths, solving the existing deterministic problem.
Reference List
Ahn, H.-S. et al. (2018) ‘Analysis of deterministic control and its improvements for an inventory problem with multiproduct batch differentiation’, Operations Research, 66(1), pp. 58–76. Web.
El Farouq, N. (2017) ‘Deterministic impulse control problems: Two discrete approximations of the quasi-variational inequality’, Journal of Computational and Applied Mathematics, 309, pp. 200–218. Web.
Maruta, I., Nishida, S. and Fujimoto, K. (2020) ‘A study on numerical solutions of Hamilton-Jacobi-Bellman equations based on successive approximation approach’, SICE Journal of Control, Measurement, and System Integration, 13(3), pp. 157–163. Web.
Schober, P., Boer, C. and Schwarte, L.A. (2018) ‘Correlation coefficients: Appropriate Use and Interpretation’, Anesthesia & Analgesia, 126(5), pp. 1763–1768. Web.
Tedone, F. and Palladino, M. (2021) ‘Hamilton–Jacobi–Bellman equation for control systems with friction’, IEEE Transactions on Automatic Control, 66(12), pp. 5651–5664. Web.