Hooke’s Law, Simple Harmonic Motion, and Archimedes’ Principle Report

Introduction

Several essential laws and processes are essential for describing forces in mechanics as a field of physics. First is Hooke’s law, which postulates that the force applied to a spring turns out to be directly proportional to the deformation at that location, as shown in equation (1). Second, it is the phenomenon of simple harmonic motion, which corresponds to the proportionality of the drag force to the object’s displacement. Hooke’s law turns out to apply to this type of motion as a particular case, when the oscillation is characterized by a period, as shown in equation (2). Finally, one of the fundamental laws is Archimedes’ axiom, which states that the expulsive force for a body immersed in a liquid is equal (or partially equal) to the weight of this body: equation (3).

Objectives

1. To study Hooke’s Law on the example of a small spring.
2. To study the possibility of determining the period of vibration of a spring as a function of mass.
3. To study Archimedes’ Principle using the example of deformation in a vertical spring.

Materials

1. Spring.
2. Ruler.
3. Stopwatch.
4. Weights.
5. Beaker of Water.

Procedure

The entire experiment is divided into three procedures, successively examining different aspects of the laws of deformation mechanics. In the first part, for ten different masses, the length of a spring was measured as a description of its deformation under the action of an applied downward force. In the second part, ten different masses were suspended from springs and subsequently pulled down: for each oscillation, the time for making a complete oscillation was measured. Finally, in the third part, a mass on a spring was lowered under water to measure the volume of water displaced.

Data tables

Table 1. Data for the first part of the experiment.

Table 2. Data for the second part of the experiment.

Table 3. Data for the third part of the experiment.

Analisys

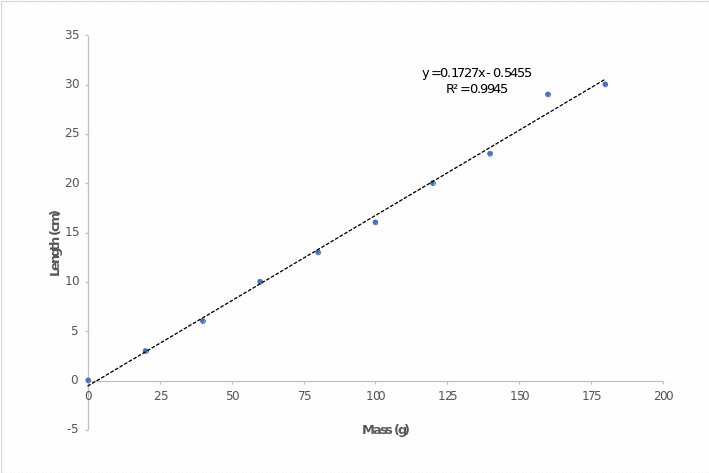
Figure 1 shows a graph of the length of the spring as a function of the mass of the weight suspended from it. It can be clearly seen that the greater the mass applied to the spring, the greater the deformation is observed, which is expressed as an increase in the length of the stretched spring. This coincides perfectly with equation (1), which postulates a linear relationship between the length of deformation x and the mass of the suspended weight in the state of equilibrium reached. The regression equation shows that the coefficient of elasticity is 0.1727.

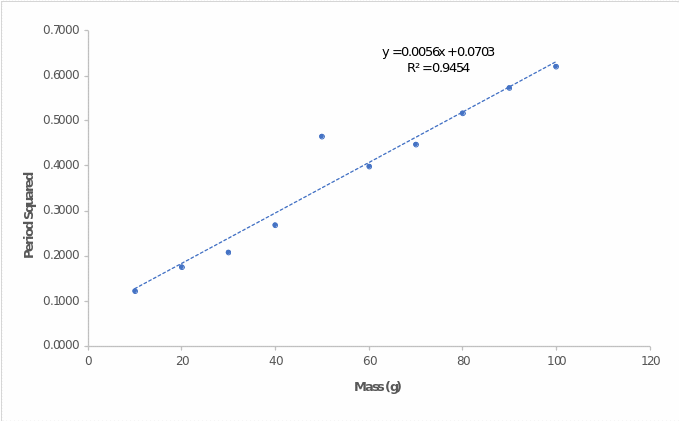
Interestingly, Figure 2 demonstrates the same linear dependence, but in this case, the square period linearly depends on the mass of the weight. In this case, the linear regression slope also corresponds to the coefficient of elasticity, but in a different form, as shown in equation (4). Consequently, the slope is 0.00566, and the elasticity coefficient is determined according to equation (5).

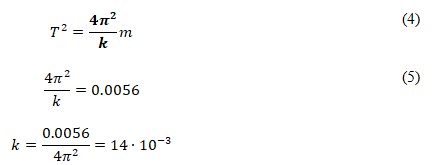
It can be seen that the elasticity coefficient for the first and second parts differ significantly, which may indicate errors in data collection.

For the third part of the experiment, it has been plotted the dependence of the change in the length of the spring as a function of the volume of displaced water. According to Archimedes’ principle, the heavier the body, to a known limit, the greater the volume of water it displaces, and the greater the deformation of the suspended spring, as was shown in the first part of the experiment. According to the laws of mathematics, a larger volume of water displaced leads to a more considerable deformation of the spring, as shown in Figure 3. In this case, the coefficient of elasticity k is defined as the slope of the graph and is equal to 31.021.

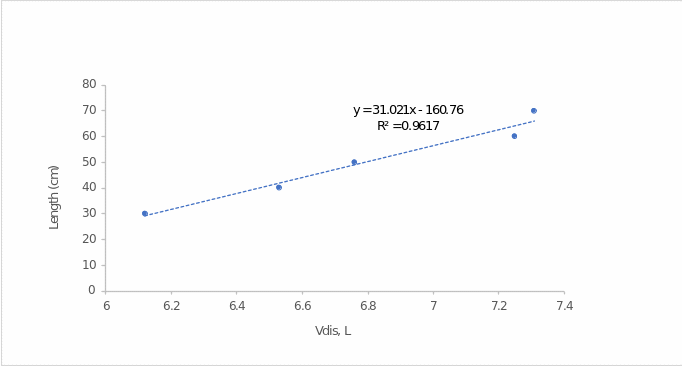
Conclusions

In the present work, a study of the properties of deformation has been conducted on the example of a spring subjected to the action of external forces. All the fundamental laws of physics were confirmed, and graphs of linear dependence were obtained for each of them. Thus, the length of deformation of the spring linearly depends on the mass of the suspended body, according to Hooke’s Law. The square period of vibration linearly depends on the mass of the suspended body, which also followed from the formula for calculating the period. Finally, it was deduced that the length of deformation of the spring would depend linearly on the volume of water displaced, according to Archimedes’ Principle.