When teaching children to choose the right strategy to memorize basic facts, it should be considered that children choose different strategies. However, children should “attempt to memorize facts only after understanding is attained” (Reys et al., 2008, p.196). Children come to such understanding quicker if they have a physical experience.
The “Abacus” game was suggested to address the need to use physical experiences during the class. This game helps children to understand how basic facts are attained. Adding and subtracting beads, children memorize by using visual memory. The game can be played in any classroom regardless of computers availability.
Another game suggested by the National Library of Virtual Manipulatives is “Factor Tree”. This game addresses the need to drill knowledge. As it has been stated by Reys et al. (2008) drill “is not the time for explanations” (p.196). While playing this game children should quickly recall basic facts. Children drill basic operations by multiplying and dividing. According to Reys et al. (2008), problem-solving is one of the best strategies to help children attain basic skills. Kids face particular challenges that excite them.
When teaching multiplication children form a background for learning division since multiplication and division are based on the same principles.
I do not agree with the statement since children should rely on physical experience as claimed by Reys et al. (2008), and counting fingers is the most available one. Thus, when they only start learning to count, children need to use fingers.
I agree since if a calculator is available all the time, students can find it easier to use a calculator to calculate even those computations which should be solved mentally. This may cause losing basic skills since no drill is available during the class.
Counting back can be an effective strategy when units’ digits are involved. For example, it can be helpful when computing 10 – 4, 25 – 2, 59 – 5. However, this strategy is not effective in cases involving tens and hundreds, etc. when it is necessary to compute 65 – 34, 165 – 127, 845 – 631. It can be more helpful to use separation problems or part-whole problems.
A clown had 24 balloons. 6 children saw his performance. He divided his balloons among all viewers equally. How many balloons did each child get?
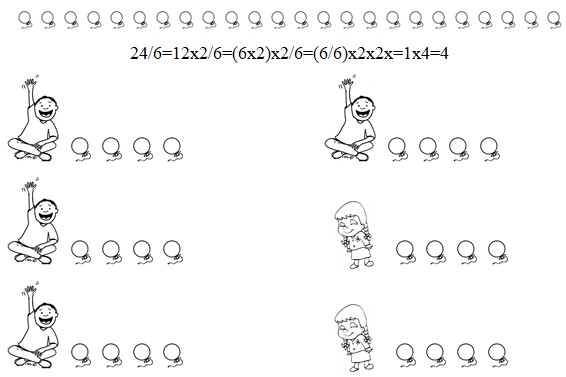
Twenty-four is twelve multiplied by two, or six multiplied by two which is multiplied by 2. Admittedly, it is easier to divide six by six, than two multiply by two, than twenty-four divide by six.
Mary bought twenty-four balloons. If she gives her six brothers balloons one by one, how many balloons each brother will get?
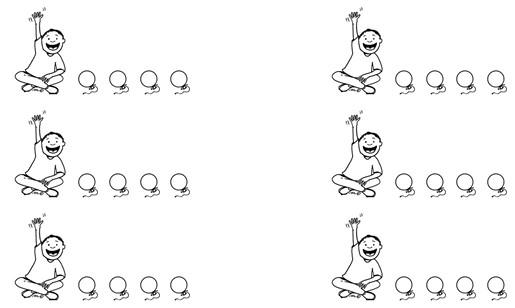
It is possible to add one balloon to each “brother”, and after this count, how many balloons each brother got.
NCTM claims that calculators should be available for students at any time (Reys et al., 2008). However, many educators would disagree, since they think that students would neglect other types of computing, relying on calculators. To my mind, students can lose major computing skills if they use calculators too often.
In many countries (and even in the USA) quite little attention is paid to computational estimation, since the focus is made on written computation (Reys et al., 2008).
The assignment is not a good one, since it focuses on the fact that computational estimation does not give the correct answer. Many students can be discouraged to use it. Reys et al. (2008) stress that it is essential to make students aware that estimation helps define whether they are moving in the right direction, rather than obtain the correct answer.
Reys et al. (2008) claim that estimation helps students understand whether they are moving in the right direction. Thus, they should be aware of the major strategies used for adjusting. They should not focus on details, but they should take into account the most significant points. Thus, if a student needs to count how much is 4235 + 6123 + 9547, he/she should add thousands to (approximately) estimate the answer.
Calculator using arithmetic logic:
- 253 – 85 / 4 = 42
- 85 / 4 = 21.25
- 253 – 21,25 = 231,75
Calculator using algebraic logic:
- 253 – 85 = 168
- 168 / 4 = 42
- 253 – 85 / 4 = 231,75
Students were doing mental computation and estimation since they had certain ideas for answering and obtaining results. All children articulated the way they were counting. The teacher helped students with certain computational methods. Students did not make up their own methods, though they chose the most comfortable one. I think the lesson was held perfectly; however, the students’ background knowledge should be considered.
This algorithm is effective, however, it is too complicated for such a simple action.

This is the most effective one, as it is universal. However, it may be improved by removing the unnecessary regrouping and adding-on part:
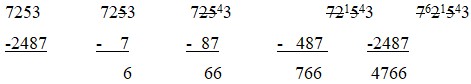
this one is too confusing.
This algorithm is effective, however, it takes too much time for solving, and does not add understanding to students.
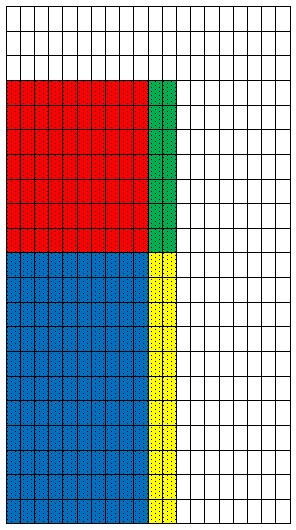
12×17=(10+7)x(10+2)=10×10+7×10+10×2+7×2=204
The diagram shows how the multiplication of two numbers may be calculated. Hence, the numbers are divided into components that are multiplied separately, and then, results added.
These subtractions should be resolved with standard algorithm described above. Children should understand the rules of subtraction, and be able to apply them in practical assignments. Therefore, making subtraction 52-25, children should realize the basic principles of math operations:
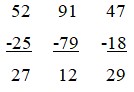
Hence, children should realize that if minuend is lesser then a subtrahend, the minuend “borrows” value from a number of a higher rank.
Their mistakes may be corrected by explaining that every following operation is performed for numbers of a higher rank. Therefore, each operation moves the numbers to higher rank. This presupposes that students need to understand the belonging of each digit of a number to a particular rank. Therefore
23* 15/115
+23/345
In fact, standard algorithms are useful for teaching students to feel the numbers, and make operations quicker. This means, that students develop the necessary way of thinking, and start solving math operations automatically, without thinking over the process in general. However, if students have an opportunity to invent their own algorithms, this will inevitably mean that they already have the necessary feeling of numbers. Additionally, the invention process will help students to overcome standard frames of thinking that will develop creativity for solving math problems. Teaching standard algorithms only will not stimulate the flexibility of thinking, while this is the key factor for solving any problems and tasks.
Manipulatives can be regarded as the necessary basis for teaching students to feel the fractions, as these manipulatives help children to attain the basic skills and physical experience which is needed for further education and training. As it has been emphasized by Reys et.al (2008), the general principles of education should involve the opportunity of independent learning and inventing. Consequently, when kids practice with squares, apples, rectangles, circles and so on, they learn to manipulate and operate with fractions, which gives them the basic understanding of fraction principles.
Manipulations are useful for studying the names and symbols of fractions, as these create images for better understanding. These images stimulate visual memory of the students, while dividing squares students learn the names of the fraction components, as we as learn to make simple math operations with these parts. Ordering fractions is performed by dividing manipulative objects into different parts (that may be compared), and then, children are offered to compare them, and decide which is bigger or smaller. Hence, they will have the basic skills for finding the least common denominator which will be needed for adding fractions with different denominators.
Therefore, the concepts associated with fractions and decimals is not simple. Nevertheless, partitioning and equivalence are claimed to resolve this problem by joining some concepts together. These concepts will help to describe the fact that 3/4 and 6/8 are equal, as well as 1/2 and 2/4.
Multiplying and dividing is reasonably regarded as a real challenge for teachers, as without proper understanding of the fractions, kids will not be able to understand the rules of multiplying and dividing fractions. Both operations are generally featured with finding a common denominator. However, multiplication produces this denominator automatically, while division requires finding it previously to performing the operation. Another way is just to explain the division of fractions is similar to multiplication as the divisor just needs to be turned upside down:

The physical models of these operations will involve explaining that division and multiplication of fractions is based on the same rules as division and multiplication of integers.
The stages identified by Hiele are as follows:
- Level 0 Visualization. This is the basic level of understanding the principles of geometry. Kids children understand that a triangle, for instance, should have three sides, and everything that has three angles or three sides will be a traingle
- Level 1 Analysis. Children that are at this level will know that sides of a triangle are straight, and lines make a closed shape. They are able to differentiate correct triangle from incorrect one. Students tart thinking applying their knowledge of shape.
- Level 2 Abstraction. Students start reasoning as for the matters of basic shapes, and they are able to find simple arguments for proving their position, and confirming the attributing of some features to particular shapes.
- Level 3 Deduction. Students learn to make the systems of proofs that are helpful for solving simple geometric problems.
- Level 4 Rigor. This level involves understanding geometry from the position of math operations. Therefore, students are able to combine their knowledge of shapes with their math knowledge.
Physical manipulations with shapes differs from virtual manipulation by principles of operating with the shapes. Therefore, physical manipulation involves senso-motoric memory as well as visual, while virtual manipulation is featured with visual perception only. However, virtual one may be featured with the opportunity to make more accurate shapes, therefore, students will learn the basic principles of making these shapes, and avoid mistakes associated with inaccurate folding of the sheets, or inaccurate drawing of the lines. Considering the teaching perspective, virtual and physical manipulations may be equal, however, learning process will be more effective if students will have an opportunity not only to see the shapes, but sense them with their fingers, fold, unfold, move, or even taste. Therefore, more perception channels will be involved, and quicker passing for the next level will be observed. In the light of this statement, it should be emphasized that the key principles of teaching should be based on involving students into the learning process as much as possible.
Reference List
Reys, R. E., Lindquist, M. M., Lambdin, D., Smith, N. L., (2008). Helping Children Learn Mathematics, 9th Edition.
National Council of Teaching Mathematics (2011). Early Childhood Corner. Nctm.org.