Kirchhoff’s Voltage Law and Its Effectiveness Report

Introduction

The investigation reported in this analysis was conducted to validate whether Kirchhoff’s Voltage Law was effective. Three resistive circuits were built to test Kirchhoff’s voltage law. The sum of voltages across various closed routes in each system and the sum of the currents at different nodes were measured.

Limitations

The experiments are limited because they operate under the hypothesis that the electromagnetic force in the closed loop system is constant. Kirchhoff’s loop criterion can be disobeyed in the presence of a fluctuating electromagnet field because electric fields and electromotive fields can be produced.

Theory

The theoretical basis of this investigation was evaluating the sum of the voltage drops throughout various closed connections, which is equal to zero. The preliminary work required was understanding the concepts of homogeneity and additively and using the digital multimeter to determine the resistor values.

Experimental Procedures

Schematic

The three figures below are the schematic diagram of the circuits involved in these experiments.

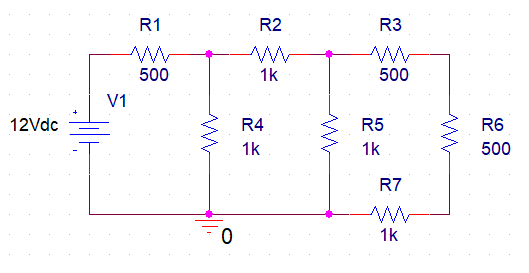
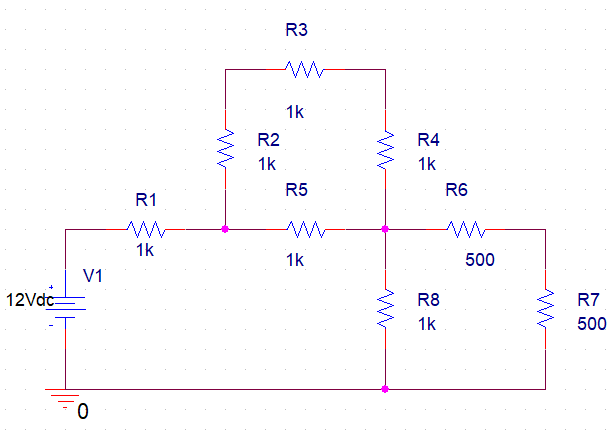
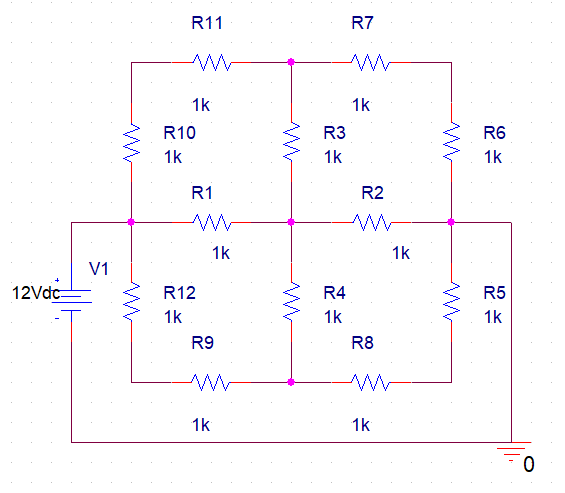
Procedure

Identify all voltage measurement nodes and execute the voltage calculations. Constructing the circuit is illustrated in Figures 1, 2, and 3. Use laboratory apparatus to measure voltage. Every measurement must be made in relation to the ground.

List of Components Used

• Breadboard
• Resistors
• Connecting wires
• Multimeter
• DC power supply

Results

The results of the figures above are presented in the tables below with voltage measurement points.

Table 1

Table 2

Table 3

Sample Calculations

Experiment 1

IR =V

I₁ (500+625) = 12V

I₁ =0.01A

V₁ =0.01A×500Ω

=5.0V

V₂ =0.01×625

=6.25V

I₂ =6.25V÷1000Ω

=6.25mA

I₃ =0.01-6.25×10^-3

=3.75mA

6.25-V₃ = (1K) (3.75mA)

V₃ =2.5V

I₄ =2.5V÷1000Ω=2.5mA

I₅ =3.75mA-2.5mA

=1.25mA

V₄ =3.75mA×1000Ω

=7.5V

V₅ =500Ω×1.25mA

=0.625V

V₆ =1000Ω×1.25mA

=1.25V

Experiment 2

I =12V÷ (1000+750+500) Ω

=5.33mA

V_{4 =}12-(5.33mA×1000Ω)

₌6.67V

V₅ = (12V×500Ω) ÷ (1000+750+500) Ω

=2.67V

V₆ = (2.67V×500Ω) ÷ (1000Ω)

=1.335V

5.33mA =3I₂+I₂

I₂ =1.3325mA

V₄₂ =1.3325mA×1000Ω =1.3325V

V₄₅ =6.67V­-2.67V =4V

V₄₅ =3V₄₂

4V =3V₄₂

V₄₂ = (4÷3) V =1.667V

V₂ = (6.67-1.667) V

=5V

V₃ = (5-1.667) V

=3.33V

I =2I₄

I₄ =5.33mA÷2

=2.605mA

V₇ = (2.667×10^-3A) (1000Ω)

=2.667V

Experiments 3

V₁ =12V, V₃ =0V

At node 2,

4V₁-V₅-V₈-12 =0 … (1)

At node 1,

2V₂+V₅-V₈ =48 … (2)

At node 8,

V₂-2V₈-6 =0 … (3)

From (1) and (2),

7V₈-V₅ =36 … (4)

Adding (2) and (3),

5V₈+V₅ =60 … (5)

Adding (4) and (5),

12V₈ =96

V₈ =8V

V₅ =-5(8) +60

=20V

V₂ =2(8)-6

=10V

V₇ =12-[(12-V₈)/2]

=10V

V₄ =12-[(12-V₅)/2]

=16V

V₆ =V₅-V₅/2

=10V

V₉ =V₈-V₈/2

=4V

Interpretation

The experimental measurements were much higher than the expected results from the calculations. The values were not precisely zero when combined. However, this was anticipated due to experimental error when connecting several components. The idea that series voltages added up made no difference, but from observation, the polarity of these voltages significantly affects how the numbers are added. Since the polarities of each voltage drop are in the same direction (Salam, & Rahman, 2018). Although the cause of this discrepancy is uncertain, the wrong connection of the multimeter might have contributed to giving inaccurate readings. Variability in the resistor and voltage source values was another factor that might have caused errors in circuit measurements.

Conclusions

In summation, in a complex circuit where all voltages around a particular loop are known, Kirchhoff’s voltage can be employed to determine an unidentified voltage. The law failed to predict the total sum of the voltage drops along closed circuits under consideration due to experimental errors.

Reference

Salam, M., & Rahman, Q. M. (2018). Electrical Laws. In Fundamentals of Electrical Circuit Analysis (pp. 25-73). Springer, Singapore.