Laying Pipelines Under the Sea Research Paper

Introduction

Laying pipelines under the sea for transportation always requires a lot of money. This often calls for creative means of installation in order to not only reduce cost but also increase on efficiency of the pipelines and cater for issues like the vortex shedding and hydrodynamic forces (Bruke, 2009). Pipelines laid offshore are usually laid directly on the seabed just intermediate to deep water in efforts to reduce cost.

Pipelines are often meant to touch the sea bed but this is not always the case as the sea bed is often not flat causing some sections to be hanging off the sea bed a concept referred to as free spans. In evaluating the hydrodynamic forces on the pipelines, the sea bed is often assumed to be plane and the pipelines touching the sea bed.

This is done because it is critical that the hydrodynamic forces in the pipelines be calculated during the design process of the pipelines and is also critical in decision making during the installation process.

In attempts of reducing the installation costs of pipelines and for other technical reasons, different pipelines of varied or similar diameters are often installed together in a bundle under the sea bed. It helps to reduce costs as well as to ease the maintenance process (Wilcox, 1994). Normally, smaller diameter pipelines are often installed besides already installed bigger diameter pipelines hence forming the pipeline bundle.

The pipeline with a bigger diameter is often referred to as the main pipeline or primary pipeline while the other pipeline(s), often smaller than the main pipeline being referred to as secondary pipelines. The bundle is often strapped together at particular points and laid on the sea bed together.

S one can notice, this will reduce installation costs by a huge difference since the money that would have been otherwise used to install the different pipelines is used to install the single bundle hence saving on costs and time. Generally, the pipelines may be in direct contact with one another or placed close together depending on the engineering technique employed during the installation process (Zdraykovich, 1987).

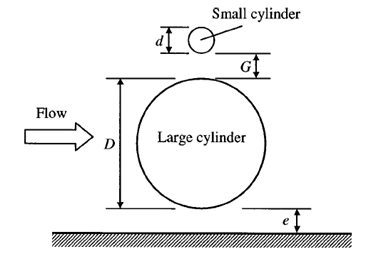
This form of installation is normally used on the gas and oil industry and is often referred to as the piggy back pipeline. Below is a figure demonstrating how the piggy back pipeline is designed. This present paper seeks to study the piggy back pipelines into details and to assess and evaluate the rationale behind such a design using appropriate calculations and examples.

The paper seeks to assess the effects of the hydrodynamic forces on the piggy back bundle and on the single pipelines forming the bundle. This will give the rationale behind this kind of layout or design. As mentioned earlier, the consideration of hydrodynamic forces will be critical in the design and installation of the pipelines. The paper will use make several unconfirmed assumptions in the process of calculations (Bruke, 2009).

The assumptions are included in this statement: that bundle will be regarded as a single pipeline depending on the proximity of the pipelines and the fact that they are installed together. The diameter of the bundle will be equal tot het combined diameters of the two pipelines and the space between the pipes if they are separated.

This will aid and simplify the calculation process and can be justified as the bundle may e regarded as operating as a single unit. Previous research indicates that vortex shedding can be suppressed at very small ratios. In fact, the smaller the gap ratio the more the vortex shedding is suppressed.

This paper investigates numerically a boundary layer which is between two cylinders which have differing diameters and near a plane or wall (Course, 2008). The two cylinders under investigation by this paper are laid in the piggy back format where the small and the big diameter cylinders are placed adjacent to one another and the ratio of their diameters kept at a constant 0.2.

The Reynolds number anchored on the pipeline with the larger diameter is kept at a constant value of 2.0_10₄. Different values in the different ratio are placed under investigation and the effect of each value ratio is recorded for comparison.

This will help the paper to deduce on the effects that take place at each ratio and thus forming a view on how different ratios impact on the bundle.

This will help form a view on the best ratio to employ during installation and during the design of the bundle. It is important to note that in this experiment, the secondary pipeline is placed above the primary pipeline and the diameter ratio is kept constant all through (Mcneill, 2009).

The figure below indicates the design of the bundle under investigation by this current paper.

Literature Review

Previous investigations have given some results that this paper seeks to confirm or contradict. Experiments by (Zhao, 2005) seem to concur that vortex shedding is lesser at small gap ratios as compared to big gap ratios. The suppression of vortex shredding is mostly observable at the ratio 0.3 between e/D that is, the distance between the bigger pipeline and the flour (e) and the diameter of the bigger pipeline (D).

It is however important to note that the experiments in this research were conducted at high Reynolds numbers. Taneda, (1965) carried out an experiment on the suppression of vortex shedding neat a plane wall for R_170. It is important to underline the fact that this is a plane wall which may not form a natural base for pipelines under the sea bed.

Zdraykovich (1987) states: that a decrease in the Reynolds number leads to an increase in the vortex shedding suppression at the gap between the cylinder and the wall. The experiment that ascertained this was carried out at Reynolds numbers that range from 80 to 1,000. The above experiments were conducted on the cylinders with different diameters.

This leaves a question of whether a replica in results will be witnessed if the experiment was carried out with cylinders of similar diameters. (Williamson, 1985) conducted a study with two cylinders of an identical diameter placed side by side. This is also another difference between the former experiments which placed the two cylinders one below the other.

The side by side arrangement is also asymmetrical prototype forming one of the flow features of this new design. (Wilcox, 1994) found that wakes flop randomly between two identical cylinders. (Tsiolakis, 1982) investigate pairs of two closely placed cylinders and had findings which found that vortex street occurred just behind the cylinders.

(Zhao, 2005) investigated flow around two cylinder of different diameter, the investigation was numerical and was carried out at two different Reynolds number values. The impacts of the pipeline with a smaller diameter on the flow around the forces were investigated.

The experiment ensured different position angles, different diameter ratios and different gap ratio. The side by side placing of the cylinders elicited a lot of interests in terms of vortex shedding and hydrodynamic forces.

Objectives

1. This current paper seeks to study the influence of a small pipeline on the hydrodynamic forces of a piggyback pipeline system. This is with a view to aid in the design and installation of the sea bed. Piggy back pipeline should be able to last after installation in order to serve the purpose for which it is installed.

It should be able to also ensure the reduction of costs both in the long term and in the short term and most importantly, piggy back pipeline should be able stand the pressure and the wear and tear it faces under the sea bed. Vortex shredding should be at the most minimum or not at all there to allow for the pipeline to last under the sea bed.

2. To determine the effects of the position angle of the small cylinder on the forces on the piggyback pipeline. Different position angles have different effects to the flow of fluid through the bundle.

As was discussed in the above researches in the literature view section, when the pipelines are placed side by side to one another they have different characteristics in the flow and vortex shredding is observed to a particular extent.

Similarly, when the smaller pipeline is placed above the bigger pipeline it shows different effects. Therefore this paper, as one of its objectives, seeks to investigate the best angle with which to place the cylinders and have the least negative effects on the bundle such as vortex shredding.

3. To determine the effects of the small pipeline on the vortex shedding frequency of the piggyback pipeline. The piggyback pipeline often faces a lot of vortex shedding and this may lead to lack of full operation of the equipment at given times.

This is normally causing inconveniences on the part of engineers in terms of maintenance and also the economist in term of costs. This therefore calls for the assessment of the extent of impacts caused on the piggy back pipeline by the small pipeline.

The smaller cylinder might e increasing the Vortex shredding or reducing it at particular gaps, therefore we need to know the exact points where these happen hence the experiment. Apart from the literature review, we need an independent research to ascertain or contradict their findings.

4. To recommend a design of the piggyback pipeline. As mentioned earlier, the effects on the piggy back pipeline placement is important as it affects several economies as it does all our safety.

If the gas company were to ignore the effects on the pipelines there could be gas leakages and this would lead to devastating results to the sea life and also the human life in general.

As such, this paper seeks to recommend the most appropriate design with which the bundle of the piggy back should be designed in order to maximize on its operations. The recommendations are going to range from the appropriate gap range to the appropriate angle with which the two cylinders should be placed.

Methodology

Apparatus

• The study was carried out numerically. This is due to the lack of figures on the piggy back pipeline.
• FEM_NS2D will be used to simulate flow around two-dimensional structures. The FEM_NS2D will be used to represent the forces that act on the two cylinders at the bottom of the sea. The nature of FEM_NS2D will be able to provide the required condition bearing that it is of similar dynamic characteristics as of that at the sea bed. The two dimensional structures that will be used will represent the two cylinders under investigation.
• Different angles for the small cylinder.
• Will be looking at two different values of the gap ratio 0.2 and 0.5.

Procedure

The two dimensional structures were placed adjacent to one another at different angles while the gap is left at a particular number. The first instance the two structures were placed at an angle of 00⁰ at a gap of 0.2. The results of this condition were recorded.

The second instance, the structures were placed at an angle of 45⁰ while the gap was left at an angle of 0.2. The angle was then changed ot 90⁰ while the gap left at 0.2, the results were recorded as well. This angles were changed to 135⁰ and then to 180⁰ while the gap was always left at 0.2. this was important as it ensured consistency in the findings.

The changing of agles and leaving the gap at a constant figure to act as control helped to have the results of the findings reliable.

The next step then involved the changing ot the gap to 0.5 while and trying this with the different angles. The results were recorded for analysis.

Results

• Results @ α=00°, e=0.2, Main and Small pipelines with the Total of both
• Results @ α= 45°, e=0.2, Main and Small pipelines with the Total of both

At this point, the force vs Time Main recorded a CD of 0.6 while the CL was recorded as around 0.1 as indicated in the graphs above. For the force vs Time small the CD was a little lower at around 0.001while the CL was recorded at slightly below 0.01, that is around 0.09. The total drag and lift had a CD of around 0.3 and the CL was at around 0.01.

• Results @ α= 90°, e=0.2 Main and Small pipelines with the Total of both

At this point, the force vs Time Main recorded a CD of 0.9 while the CL was recorded at slightly below the 0.00 mark at around -0.01 as indicated in the graphs above. For the force vs Time small the CD was a little lower at around 0.13 while the CL was recorded at slightly above 0.05 that is around 0.02. The total drag and lift had a CD of around 0.5 and the CL was at around 0.00

• Results @ α =135°, e=0.2 Main and Small pipelines with the Total of both

At the above mentioned angle and gap, the force vs time and force vs Time small showed a difference in the results too. The CD at the force vs Time Main was recorded at 0.6 while the CL was recorded at around 0.19.

The force vs Time small on the other hand indicated the CD at around 0.135 and the CL at 0.125. In turn, the Total Lift and Drag of the two structures recorded CD at around 0.35 and the CL at around 0.15.

The above result seemed to be differing form the previous results and therefore the need to continue with the experiment and attain more figures for comparison purposes.

Results @ α= 180°, e=0.2, Main and Small pipelines with the Total of both

At the above mentioned angle and gap, the force vs time and force vs Time small showed a difference in the results too. The CD at the force vs Time Main was recorded at 0.65 while the CL was recorded at around 0.195. The force vs Time small on the other hand indicated the CD at around 0.015 and the CL at 0.095.

In turn, the Total Lift and Drag of the two structures recorded CD at around 0.45 and the CL at around 0.01. The above result seemed to be differing form the previous results and therefore the need to continue with the experiment and attain more figures for comparison purposes.

Results @ α= 00°, e=0.5 Main and Small pipelines with the Total of both

At the above mentioned angle and gap, the force vs time and force vs Time small showed a difference in the results too. The CD at the force vs Time Main was recorded at 0.25 while the CL was recorded at around 0.00 though it had fluctuating values of the Ut/d making the graph to form a wavy line.

The force vs Time small on the other hand indicated the CD at around -0.05 and the CL gave varied figures. In turn, the Total Lift and Drag of the two structures recorded CD at around 0.45 and the CL at around 0.00 though a bit fluctuating sometimes to -0.01.

The above result seemed to be differing form the previous results and therefore the need to continue with the experiment and attain more figures for comparison purposes.

• Results @ α= 45°, e=0.5 Main and Small cylinder with the Total of both

At the above mentioned angle and gap, the force vs time and force vs Time small showed a difference in the results too. The CD at the force vs Time Main was recorded at 0.65 while the CL was recorded at around 0.00 though a bit fluctuating sometimes to -0.01.

The force vs Time small on the other hand indicated the FX at around 0.45 and the CL at 0.001. In turn, the Total Lift and Drag of the two structures recorded CD at around 0.45 and the CL at around -0.01.

The above result seemed to be differing form the previous results and therefore the need to continue with the experiment and attain more figures for comparison purposes.

• Results @ α =90°, e=0.5 Main and Small cylinder with the Total of both

At the above mentioned angle and gap, the force vs time and force vs Time small showed a difference in the results too, they indicated fluctuating values in the g/d and the Ut/d figure with the following averages. The CD at the force vs Time Main was recorded at 1.0 while the CL was recorded at around -0.5.

The force vs Time small on the other hand indicated the CD at around 0.19 and the CL at 0.095. In turn, the Total Lift and Drag of the two structures recorded CD at around 0.55 and the CL at around -0.05. The above result seemed to be differing form the previous results and therefore the need to continue with the experiment and attain more figures for comparison purposes.

• Results @ α =135°, e=0.5, Main and Small cylinder with the Total of both

At the above mentioned angle and gap, the force vs time and force vs Time small showed a difference in the results too, they indicated fluctuating values in the g/d and the Ut/d figure with the following averages. The CD at the force vs Time Main was recorded at 0.75 while the CL was recorded at around -0.5.

The force vs Time small on the other hand indicated the CD at around 0.21 and the CL at 0.19. In turn, the Total Lift and Drag of the two structures recorded CD at around 0.45 and the CL at around 0.15. The above result seemed to be differing form the previous results and therefore the need to continue with the experiment and attain more figures for comparison purposes.

• Results @ α =180°, e=0.5, Main and Small cylinder with the Total of both

At the above mentioned angle and gap, the force vs time and force vs Time small showed a difference in the results too, they indicated fluctuating values in the g/d and the Ut/d figure with the following averages as well. The CD at the force vs Time Main was recorded at 0.65 while the CL was recorded at around 0.00.

The force vs Time small on the other hand indicated the CD at around 0.49 and the CL at -0.49. In turn, the Total Lift and Drag of the two structures recorded CD at around 0.45 and the CL at around 0.00.

I was able to calculate the Mean Drag and Mean Lift in all the cases. The Mean Drag against position angle and Mean Lift against position angle were also plotted. The RMS for both the Main pipeline and the Small pipeline were computed for analysis.

Data Presentation

Notes :-These calculations are non-dimensional.

– C_D : Drag force, C_L : Lift Force RMS: Root Mean Square.

• Calculate: C_D = F_D / (1/2*ƥDV²) , C_L = F_L/ (1/2*ƥDV²).
• Calculated the Mean C_D and Mean C_L. (From when the graphs became stable).
• RMS =√(Ʃ(C_D – Mean C_D)²)/ total .
• Mean Drag and Mean Lift vs Position angel α for main Pipeline. (@ 0.2 gap ratio)
• Mean Drag and Mean Lift vs Position angel α for small Pipeline. ( @ 0.2 gap ratio )
• Mean Drag and Mean Lift vs the position angel α for main pipeline. (@ 0.5 gap ratio )
• Mean Drag and Mean Lift vs the position angel α for small pipeline. ( @ 0.5 gap ratio )
• Root Mean Square v/s position angels α for main pipeline. ( @ 0.5 gap ratio )
• Root Mean Square vs position angels α for small pipeline. ( @ 0.5 gap ratio )

Conclusion

This current paper has managed to investigate the flow of fluid over two cylinders placed in a piggy back design. This has been done numerically as has been indicate above.

The Vortex Shedding is governed by gap ratio. In our investigation, we conclude that the vortex ration is in a large extent governed by the gap ratio. This is the distance from the ground to the cylinder. The gap ratio of 0.5 indicated more of the Vortex shredding while the 0.2 gap gave a lesser vortex shredding effect.

It is therefore important to mention that placing the two cylinders closes to the ground is likely to be more effective in terms of avoiding the vortex shredding effect. There were modes of vortex shedding that were quantified and identified as the function gap ratio (Mcneill, 2009).

The effects of the Mean Drag and Mean Lift Coefficients and the mode of the vortex shedding affect the coefficients on the cylinders. This is because when the smaller diameter cylinder is experiencing vortex shredding the coefficient forces on both the two cylinders fluctuates as shown in the graphs above at frequencies that correspond to those of the smaller pipeline.

When the two cylinders behave as a single body as in the case of bundles, then the coefficient force fluctuate at frequencies identical to those that would otherwise correspond to a pipeline of the a diameter of the combined cylinders (Taneda, 1965). But, when vortex shredding processes are two, then the force coefficient fluctuate at a combination at frequencies that are similar to those that emanate from the two cylinders.

Increase in the ratios of the diameter of the big cylinder (D) and the distance from the ground (e) increases the drag coefficient on the cylinder with a larger diameter (primary cylinder) (Bruke, 2009). How the mean drag varies on the larger cylinder with G/D is anchored on the value of e/D already described above.

An increase in the e/D leads to a decrease in the mean lift coefficient on the large cylinder, the increase is sharp when the G/D is lower than 0.2. But when it reaches 0.2 and still is increasing, the change becomes less sharp till exponential.

Since no Vortex shredding exists in the section of e/D-0.2 and 0.3, the RMS coefficients are 0. In the case of e/D=0.5, the lift and drag force coefficients on both cylinders will always have a value of greater than 0.

However, it is important to note though that the gap ratio has a small effect on the small cylinder’s RMS force coefficients for a G/D-0.2. The mean drag force is biggest at α = 90° while the lift force tend to be lowest at the same angle (Mcneill, 2009).

Importance of this study

The study has helped in the understanding of the design and the installation of the pipelines and how they should be done at a minimal cost on the maintenance of the pipelines. As was required by the objectives of the study, the effects of the small cylinder on the hydrodynamic forces have been ascertained to the angle of placement of the cylinder against the big cylinder.

The paper also sought to determine the effects of the position angle of the small cylinder on the forces on the piggyback pipeline which the paper has achieved. This has happened to all the objectives of the study as has been discussed in the conclusions (Zhao, 2005).

Recommendation

The small cylinder should be located on the opposite side of where the force is hitting the main pipe. This will help shield the small pipe from direct hit by the hydrodynamic forces and hence reduce the cortex shredding effect.

And thus during installation, the angle to which the small pipe is placed should be dictated by the direction from which the force is coming; it should then be placed in a manner able to shield it from the turbulence.

The pipelines should be as close as possible to the seabed. This is also to reduce the lift force on the pipelines and to ensure less damage due to effects emanating from drag force. Placing the bundle closest to the sea bed also helps stabilizes the bundle and as such the bundle is able to last and require less attention for maintenance (Mcneill, 2009).

References

Bruke, J. 2009, Report writing, Cengage, New York.

Course, OU, 2008, Thinking Critically, Open University Worldwide, New York.

Mcneill, SC, 2009, Research Methods: Third Edition, Cengage Learning, Chicago.

Taneda, S, 1965, Experimental investigaion of Vortex Streets, J.Phys, Japan.

Tsiolakis, E, 1982, Reynoldische Spannungen in einer mit einem, Dortmund Publishers, Berlin

Wilcox, D, 1994, Simulation with transition with a two-equation turbulence model, AIAAJ, New York.

William, m, JP, 2006, Research Methods Knowledge Base, Cengage, Chicago.

Williamson, C, 1985, Evolution of a single wake behind a pair of bluff bodies, J. Fluids, Japan.

Zdraykovich, M, 1987, The effects of interference between crcular clinders in a cross flow, J. Fluids, Japan.

Zhao, M, 2005, Numerical simulation of viscous flow past a bundle of two cylinders of different diameters, Apple Ocean, New York.