Optimisation Modelling to Enhance Operational Efficiency at Manufacturing Companies
Manufacturing companies currently manage a large number of business processes of various kinds. Maintaining competitiveness in a constantly changing environment is an urgent and, at the same time, multicriteria task, often depending on many external factors. However, despite the complexity, organizations often change to optimize these processes. To adapt them to modern requirements, advanced technologies are used that are rapidly developing or new methods in individual sectors: HR, logistics, innovation, and much more.
Among these methods, the most well-established include systems analysis and modeling. These techniques have long been shown to have a vast potential for use in business due to their explanatory and predictive functions, which are critical for understanding the complexity of business processes (Mitroff et al., 1974; Pidd, 1997). Despite the identified number of systematic approaches to operations, their specificity is sometimes polarized depending on the methods, technologies, or subject area of business use.
Optimization models began to evolve along with the leap in hardware and software. Not only independent, comprehensive systems, including accounting, sales control, transport schemes, and much more, have been received by many enterprises worldwide, but also more straightforward tools, the capabilities of which have greatly simplified part of their activities. For example, spreadsheets combine the functions of complex calculations and mathematical operations into statistical methods (Baker, 2016).
Industries that need to optimize multiple processes at once and coordinate them with each other in time and departments can build Gantt charts, calculate supply by demand, seasonal factors, plan costs and revenues, and much more (Albright & Winston, 2005; Baker, 2016 ). By receiving information using this software, management made decisions and changed the operational activities of departments. In addition, spreadsheets made it possible to organize and control previously scattered data, which was not subject to corrections, and store, as a rule, in handwritten paper form.
Logistics, being such a complex science, also needed modeling. In addition to the obvious possibilities for calculating delivery times and building the most optimal routes and networks, technologies provided the functionality of taking into account risks when creating a model (Reveillac, 2017). The system’s complexity, as the goal of the most realistic model, was achieved through the consistent implementation of economic and mathematical mechanisms and techniques and, later, the methods of system analysis and informatics (James, 2021). Technologies such as big data, artificial intelligence, or neural networks that can be trained on different samples have taken logistic models to a new level. They have become able to be controlled and managed in real-time, independently calculate the optimal opportunities for specific input data, and much more (James, 2021; Reveillac, 2017).
As a result, to remain competitive, all enterprises must, to one degree or another, implement optimization models for several business processes. These include financial management, HR, supply chain, production with the inclusion of certain specifics, and much more. Over a long period of research, many approaches have already appeared that can decompose the process into components and provide information from various points of view. In today’s world, where global challenges play a significant role in influencing business and technology becomes an indicator of progress and development, constant optimization is critical to maintaining market positions.
Linear Programming Model
In this paper, we consider the logistics system of one of the enterprises, which can be optimized by the indicated means due to its complexity. First of all, it is necessary to designate this problem as a classical transport problem in the subject area of optimization methods. The transport problem is a mathematical linear programming problem, particularly about finding the optimal distribution of homogeneous objects from the accumulator to the receivers while minimizing the cost of moving (Moutinho & Huarng, 2015).
The transport problem can be solved in various ways and with software. As a rule, MATLAB packages or Excel spreadsheets are used for this (Anderson, 2016). The solution comes down to choosing the most optimal value for the linear function, the minimum extremum point, and the lowest possible transportation costs in the applied context. Although in the classical form, the task has a less complex structure, unlike fundamental business processes, there are various possibilities for adaptation. For example, in this case, there are intermediate points that are beneficial in terms of transportation but have storage restrictions. Moreover, the most obvious difference lies in the ranking of the transported products, which creates the need to solve the problem iteratively.
This paper defines six variables: warehouse, retailer, product, factory, units, and cost price. The classical transport problem involves the availability of stocks in warehouses and the specifics of the throughput of intermediate points with the overall goal of supplying the final points with the necessary volume of products. Linear programming is a branch of mathematical programming that studies methods for solving extremal problems characterized by a linear relationship between variables and a linear criterion (James, 2021). Combining optimization possibilities with the help of linear programming, one can get the most optimal routes that minimize costs. The linear relationship between the variables is apparent: the duration and distance of the journey determine the number of costs.
The task will be solved for each product, of which there are only three. Each product travels from the factory to the retailer, with the ability to get through warehouses. In this case, it is necessary to take into account the possibility of direct delivery from the factory to the client. This model can only work under several restrictions. Firstly, the cargo must be equal at all stages of transportation to the volume sent.
Secondly, factories and warehouses have their capacity, while each retailer has its own demand for each product, which cannot be exceeded. As part of the work in Excel, restrictions were also indicated in traffic volume values greater than zero, and the number of products must be set to integers. At the moment, a possible solution to the problem lies in the plane of the iterative approach.
First, the most optimal placement of the product in warehouses is determined by the possibilities of their filling, and then the problem of linear programming for warehouses and retailers is solved. Finally, the rest of the demand is distributed by optimizing the delivery from the factories. The result is three tables with three objective functions for optimizations within each product. After the second iteration or step, restrictions are also calculated for products that have already satisfied demand or have already been sold through warehouses. Figure 1 shows the solution to the problem for the first product.
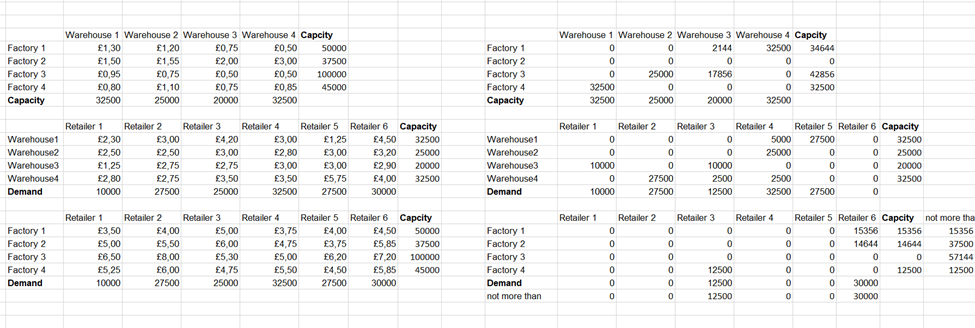
The progress of the work is the creation of convenient tables of initial data, from which data for three offset tables are taken, as in Figure 1. The construction of the function for optimization is carried out according to the SUMPRODUCT () formula, which returns the sum of the product of the array elements, which in this case is the price of transportation multiplied by the number of items shipped. Limits in the tables on the right are set using the SUM() function, which must be less than or equal to the corresponding demand or capacity values from the tables on the left, where prices are indicated.
In this case, the task was to complete the sale of products from warehouses on demand, while the remainder was sold by the remnants of capacity from factories. Less than or equal limits apply to factory capacity values in the first table, demand in the second table, and again factory capacity in the third table, while the other values must be strictly equal in the two tables. Thus, there is a check of the number of goods at each stage of transportation and the need to satisfy the demand of each of the customers with each product. Therefore, the linear function itself, in general, has the form where F is factories, W is warehouses, and R is retailers:
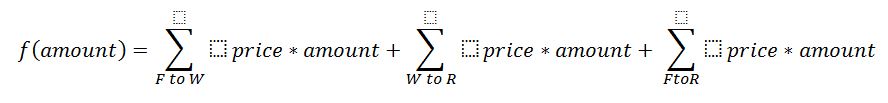
This system model is tested at each stage. Products are first distributed to warehouses as far as possible, then sold from warehouses to meet customer demand. This route was chosen primarily due to the fact that transportation from warehouses is usually more profitable than direct delivery from production. Secondly, the rest of the demand is saturated with delivery from factories, after which all costs are summed up. The results will be presented and discussed in the next chapter.
The technique is imperfect since it does not consider the potential dynamics of parallel sending and optimization, considering multicriteria. The product can be shipped directly at once, and in some situations, shipping is cheaper. However, a search for a solution in Excel for a table exclusively of demand and sales from factories showed that, in this case, delivery is much more expensive than through warehouses.
In this way, the value of a given staging point in the supply chain is realized, and this method can show the need to expand warehouse property, or real estate itself, by predicting costs with a known demand (Russell & Taylor, 2010). This kind of analytics is critical in the practical field of almost any production due to the flexibility of methods (Laursen & Thorlund, 2016). Considering that the model itself has the potential for improvement, its importance in constructing the most optimal routes is difficult to overestimate.
Since each warehouse has a specific stock for each product, an iterative approach becomes justified. Otherwise, complex calculations of the highest priority warehouse filling with one of the three products would significantly complicate the calculations, which had to be integrated into a more complex information environment, unlike Excel. As a rule, the classical transport problem of linear programming can only take into account the ranking of stocks and the ability to bypass intermediate points if they are strictly specified.
More complex systems for working with transport and logistics tasks can provide a more complex solution with a large number of input data. The solution proposed using spreadsheets optimizes the cost price variable, which is presented in the objective function as the sum of the products of costs and the number of units of goods transported. In each case, the function is optimized by finding the minimum under given constraints on warehouse capacity, production scale, and customer demand.
The variables of factories, warehouses, and retailers are presented to identify the limitations of their characteristics – capacity and demand – and are more illustrative in Excel’s framework for solving this problem. After obtaining the minimized sum of costs for each iteration, all costs for the three products are also summed up and presented as a solution to the transportation problem. This value is compared with the company’s current costs, and further steps are discussed with the management to implement the optimization model for fundamental business processes.
Results
Table 1. Results.
As a result of an iterative approach to solving several linear programming problems, the results presented in Table 1 were obtained. In the applied context, they must be compared with the company’s actual costs for the transportation of these products. Figure 1 above shows a detailed solution with the distribution of goods for the first product. Figures 2 and 3 below show the resulting tables for products 2 and 3, respectively.
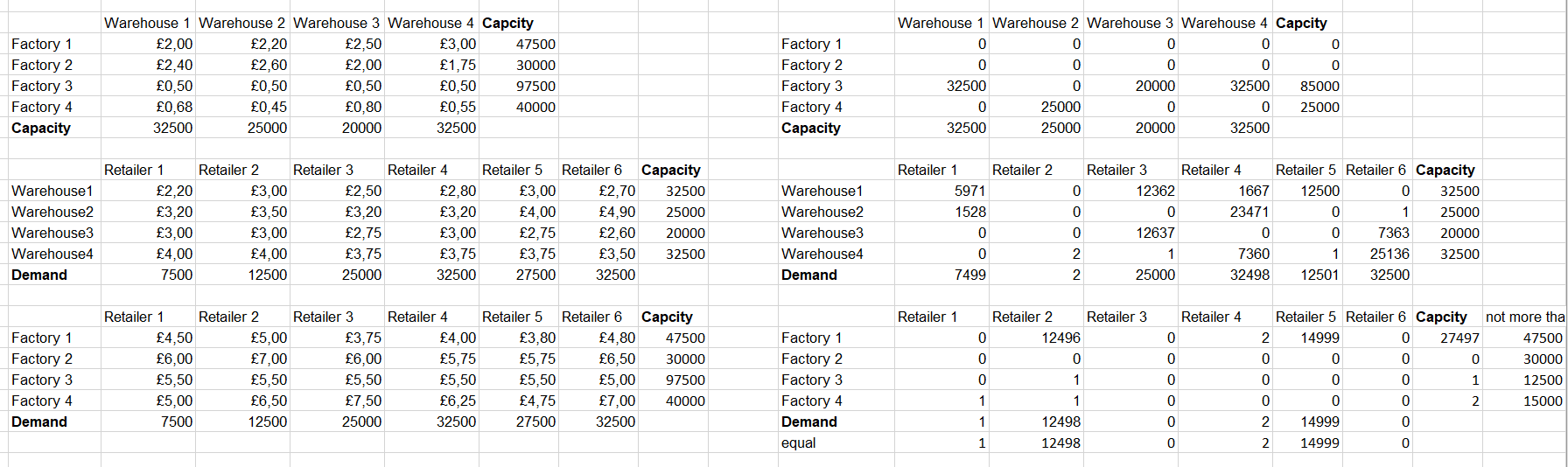
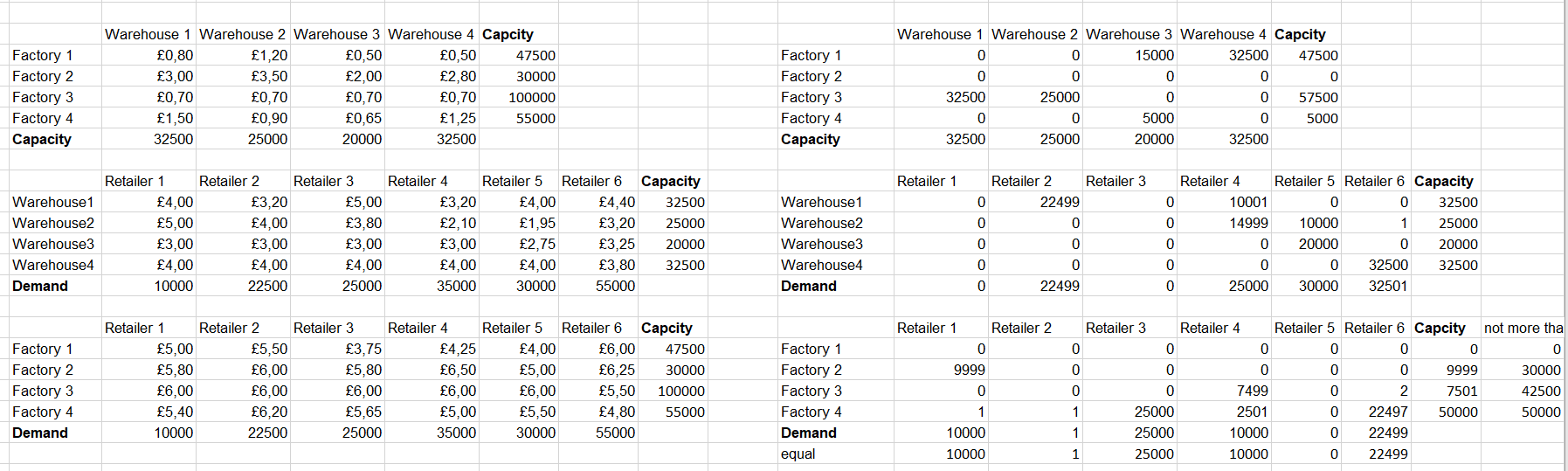
This model has several advantages. Firstly, it considers all the indicated costs and can be easily recalculated for new input data when referring to the corresponding cells. Secondly, in contrast to the classical transport problem, the iterative approach allows taking into account some restrictions, intermediate points, and ranking of goods, even though, in fact, at each iteration, the task is reduced to the simplest possible. As a consequence of the advantages, this model has many limitations or weaknesses. First of all, the model does not take into account a dynamic integrated approach: in this situation, the company necessarily distributes the maximum load of products to warehouses, although in some situations, a more flexible and adaptive approach is possible with the transition to transporting goods directly to customers, leaving a reserve storage space. In addition, when distributing goods among warehouses, the model does not consider the potentially high cost of delivery to retailers from factories, which are left without satisfying demand as a result of solving the second table. These limitations only emphasize the complexity of the data and the potential for model development.
At the same time, there are several restrictions on transportation, which the model takes into account. First, warehouses are filled with goods from each factory, but no more than the amount the factory can produce. Secondly, all goods are sent from warehouses to customers, but no more than the demand of each retailer and no more than the current number of units of goods in warehouses. Then, the balance of goods in the factories and the needs of customers are checked. This difference is made up of deliveries from factories, which are no more than their available balance of production by an amount equal to the remaining demand. This model passes the sensitivity analysis due to the introduced restrictions, and the construction of the spreadsheet makes it possible to calculate this search for a solution on new input data.
However, it is also worth mentioning the potential limitations in the form of various external factors and emergencies. The model does not include in these calculations the risks that may be associated with vehicle breakdown and more severe political restrictions, such as lockdowns and restrictions on movement. In various situations, these losses can lead to a delay in time, damage to products, increase in tariffs. The solution to this problem may lie in the plane of introducing risk coefficients calculated based on empirical observations and setting mandatory costs at specific intervals. However, such a model requires more serious software and can hardly give an accurate assessment using Excel.
Benefits of Transportation Planning and Optimization Software
Excel has a simple and accessible interface with the most commonly used functions. However, in the context of optimization methods, this software has several advantages exclusively within the framework of analytics and data analysis. Its features in finding solutions could be more extensive and sometimes more convenient when compared to SPSS or MATLAB. Even though these packages have a more expensive license and a much less intuitive interface, they provide many more options for optimization methods, including Monte Carlo, multivariate regression, and much more.
MATLAB can process vast amounts of data relatively quickly, which can also be presented graphically. Excel could be handier when working with enormous amounts of data. SPSS is more focused on statistical methods and is required when it is necessary to find a correlation between non-obvious indicators of production and, for example, financial relations. The proposed transport problem is best solved using MATLAB tools, while Excel will be helpful in small calculations of related tables.
Therefore, if a company has an extensive product database and, as a result, a more complex logistics system, it will need MATLAB as a more suitable tool for working with more data and implementing more complex methods. Excel is suitable for an organization’s financial reporting, where relatively simple relationships are calculated at various time intervals. Finally, SPSS will be required to evaluate and control sales, demand, and marketing and find their correlation between various production or financial indicators or to process survey data, such as employee satisfaction, within the company. All software has its tasks, but it is necessary for the company’s sustainable development.
References
Albright, S. C., & Winston, W. L. (2005). Spreadsheet modeling and applications: essentials of practical management science. South-Western Pub.
Anderson, D. R. (2016). Quantitative Methods for Business. Cengage Learning.
Baker, K. R. (2016). Optimization modeling with spreadsheets. John Wiley & Sons.
James, R. E. (2021). Business analytics: Methods, models and decisions. Pearson.
Laursen, G. H., & Thorlund, J. (2016). Business analytics for managers: Taking business intelligence beyond reporting. John Wiley & Sons.
Mitroff, I. I., Betz, F., Pondy, L. R., & Sagasti, F. (1974). On managing science in the systems age: two schemas for the study of science as a whole systems phenomenon. Interfaces, 4(3), 46-58.
Moutinho, L., & Huarng, K. H. (Eds.). (2015). Quantitative modelling in marketing and management. World Scientific.
Pidd, M. (1997). Tools for thinking—Modelling in management science. Journal of the Operational Research Society, 48(11), 1150-1150.
Reveillac, J. M. (2017). Modeling and simulation of logistics flows 1: theory and fundamentals. John Wiley & Sons.
Russell, R. S., & Taylor, B. W. (2010). Operations Management: Creating Value. John Wiley & Sons.