Abstract
The paper sought to analyze the physiologically-structured population models and their ordinary differential equations reduction. It includes the formulation of a physiologically structured model of the population as a non-autonomous linear integral equation of the population level birth rate (Diekmann et al., 2019). The study seeks to find out when the model that is structured physiologically allows reduction to an ODE that does not involve losing relevant information.
Description of the Problem
There are models which have been developed but have not considered the reduction of a population in a more detailed structured population. The paper seeks to solve the problem of understanding the conditions under which the individual processes against survival, growth, and fission do the developed equations lead to an honest representation of a cell-based model that is size-structured (Diekmann et al., 2019). The particular focus is on cell fission into two parts that are equal. The derivation of an ODE system through the description of the asymptotic time behavior of the population death, reproduction, growth, and depends on the environmental condition, and it is mainly through a single common factor.
The developed problems are as below:
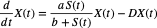
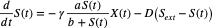
Where:
- X(t) refers to the bacterial biomass and
- S(t) is the substrate concentration in the growth tank at time t
The model was formulated while considering bacterial biomass and not considering issues concerning cells individually. It considered the assumption of results that are substrate in how cells grow and specifically not directly focusing on cell fission. In addition, the issue of ODE-reducibility was considered from different angles and while working under restrictions that are not similar. It analyzed the birthrate at the population level while considering the assumption of a number that is finite specifically for states-at-birth and also at dynamics which are at the individual state. Furthermore, the paper gives new examples, particularly working with division or fission into two parts that are equal. There is also the promotion of equation formation that is the renewal of a structured population that is physiological in nature.
Methods Used
There are several methods used during the study in achieving the desired results. The first method used is the constructive method. It was developed for solving first order partial differential equations without non-local terms. The methods, therefore, solve the equations through generation expansion as applied in the renewal equations theory. The renewal equation took center stage through the use of birth rate history as a state. It is also through dynamical system definition through history updating (Diekmann et al., 2019). This paper, therefore, focuses on renewal equations as the beginning point in modelling populations that are physiologically structured.
Another method is through computation that involves elimination of everything that is non-linear in the combination of the present components. It, in most cases, also involves E-dependent coefficients in the process. This is followed by finding out if the remainder can be written as a linear combination of new functions of x, which is then added to the new functions as additional components (Diekmann et al., 2019). This is a generally acceptable ODE test for reducibility that begins with output functionals collection, which one requires.
New Results
The paper showed the renewal equation leads to the condition for ODE reducibility. There are equations that involve per capita growth, rates of reproduction, and death. The analysis of k=1 and k=2 specifically for fission into two equal parts, the researchers reviewed a paper submitted by Diekmann et al and realized that it was completely under specific restrictions (Diekmann et al., 2019). The paper also found the connection between the example by Diekmann (1983), the equation indicated below;
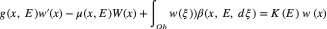
,and the example of Metz and Diekmann (1986), thus allowing for the reduction in large time behavior to an ODE. It needs proper dedication of resources for the suitable solution to occur; otherwise, the topic is open for anyone interested to pursue further studies. Scholars are also encouraged to share new findings in the field so that more researchers can utilize the literature in their studies.
Possible Extensions
Researchers should focus more on ODE reducibility as it is a field that has not been fully exploited. Its challenging nature makes it difficult for most researchers to study. This move leaves a gap that needs to be filled by new research. This, therefore, encourages researchers to venture into the field and seek out answers for the problems. Such a move contributes to knowledge that can be used in future studies. The ordinary differential equation can also be utilized by other fields’ expertise in solving the challenges they face. The reduction of order method is an area where most researchers have not fully ventured and explored. The ODE is continually evolving to make the field grow; hence any little contribution by any research can have a significant impact in this field.
Reference
Diekmann, O., Gyllenberg, M., & Metz, J. A. (2019). On models of physiologically structured populations and their reduction to ordinary differential equations. Journal of Mathematical Biology, 80(1-2), 189-204. Web.