Introduction
The present laboratory work investigates the relationship between the velocity of a picket fence falling at constant acceleration and the instantaneous value of the time it takes for this fall. Four tests were performed to collect data in which the picket fence is released in vertical free fall against a photogate, the passage of the black strokes recorded automatically. As a result of these tests, Table 1 was constructed, reflecting the time taken to pass a particular path.
Table 1: Raw data from four measurements
Analysis
For each of the four tests, it was necessary to determine the instantaneous values of time and velocity. The corresponding mean values were calculated according to the formulas given in the textbook — [1] and [2] — for the pairs of each of the seven positions (from 0.000 m to 0.300 m) and entered in Table 2.

From the last two columns for each section of Table 2, it was necessary to plot the linear dependence: a total of four graphs. The corresponding visualizations showing the linear regression equation are shown in Figures 1-4.
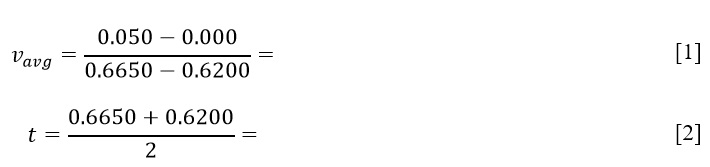
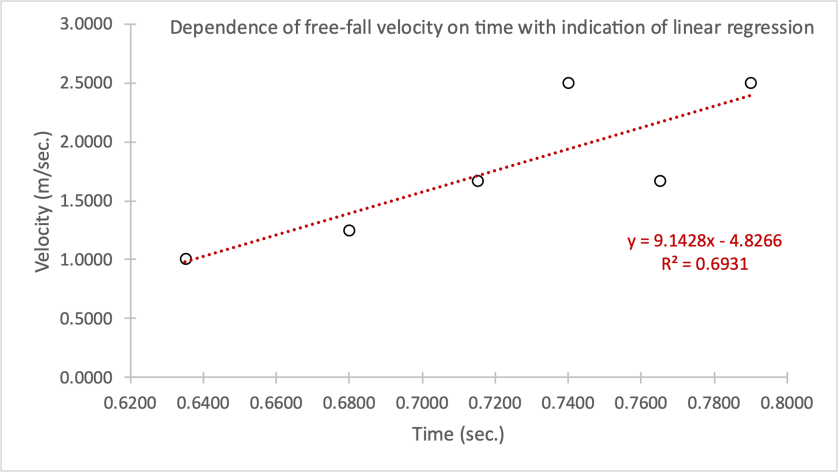
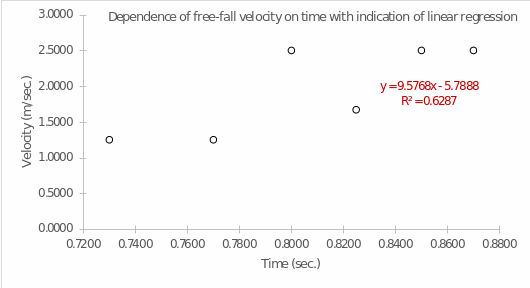
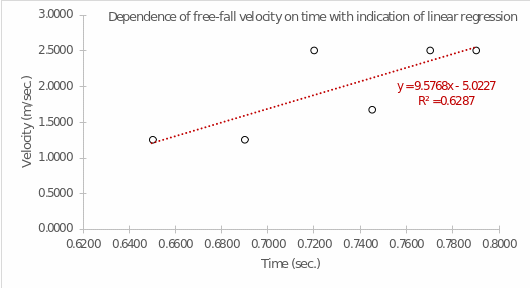
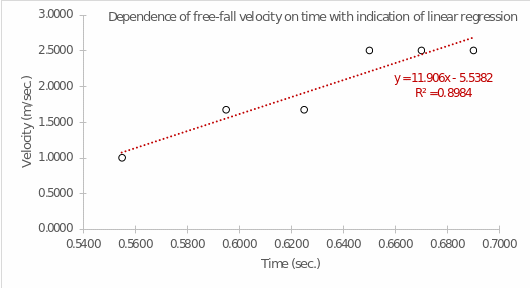
As can be seen, each regression has a different value of the coefficient of determination. The R2 coefficient determines the accuracy of the model fit: out of all four plots, the highest accuracy was true for the fourth trial, in which the regression covered up to 89.84% of the variance of the data (Fernando, 2021). The resulting equations indicate a nearly linear relationship between the variables: as time increases, so does the rate. This means that the velocity would be infinite in the perspective of unlimited fall, which is consistent with the physical meaning of acceleration. For each graph, there is a unique value for the slope coefficient, which is the rate of acceleration (m/s2) as the time parameter increases by one unit. Although all the slopes are similar, the velocity for the fourth trial changed the most. At the same time, the y-intercept values determine the speed of fall (m/sec) of the picket fence at zero time when the object has not yet committed motion. For all graphs, these values are negative, but in practice, this does not make sense because, at the zero moment of time, the objects had no velocity in this reference frame.
Conclusion
To summarize, in this laboratory work, the relationship between the velocity of fall and time was studied. It was shown that the models could be treated as linear with a sure accuracy; the equations of the corresponding linear regressions reflecting the reciprocal relationship are presented. The slope in the regression equation corresponds to the free-fall acceleration acting on the falling object. In physics, this coefficient has a value of 9.8, and the laboratory-calculated values are close to this parameter, except for the fourth test.
Reference
Fernando, J. (2021).R-squared. Investopedia.