Introduction
To be considered rational, a function must be a ratio of polynomials, with the denominator’s polynomial, not equal to zero. This is a definition of a rational number of the form p/q, where q≠0. A wide variety of real-world contexts use rational functions (Peraro, 2019). Rational functions describe the connection between velocity, range, and time, but they also find extensive application in the fields of medicine and engineering.
Additionally, a rational function is a function that may be written as the ratio of other functions, specifically polynomials. When a function has only one variable, x, it is said to be rational if it can be expressed as f(x) = p(x)/q(x), where p(x) and q(x) are polynomials with values that are not equal to zero and q(x) is less than p(x) (Lokot et al., 2021). A rational function is denoted by the formula f(x) = (x2 + x – 2) / (2x2 – 2x – 3), for instance, and in this case, 2x2 – 2x – 3≠0. Moreover, the numerators of a rational function can be constants because every constant is a polynomial.
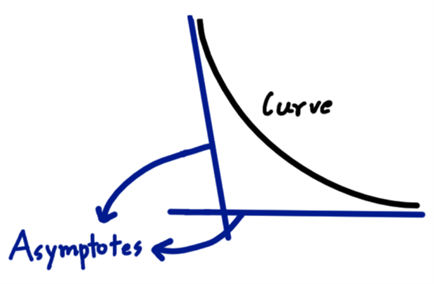
When it comes to rational graphing functions, knowing about their asymptotes is a highly vital subject under the belt. A line or curve is said to have an asymptote when it moves inexorably closer to the curve over time but never actually meets (Lokot et al., 2021). A good illustration of an asymptote can be found in Figure 1. Three kinds of asymptotes can occur in rational functions: horizontal, vertical, and oblique asymptotes.
Horizontal Asymptotes
This indicates that the asymptote is horizontal, or in other words, parallel to the axis that represents the variable that is being controlled. A horizontal asymptote for R(x) is only possible if the degree of P(x) is greater than the degree of Q. (x) (D’Hoker et al., 2019). Divide the numerator and the denominator of R(x) to find the asymptotes of the function. The next step is determining the value R(x) approaches as x goes to extremely high values. This value indicates how far above the curve the asymptote extends.
Vertical Asymptotes
As R(x) approaches the zeros of Q, the function will exhibit vertical asymptotes (x). This is because when x is at one of its zeros, Q(x) equals 0 (D’Hoker et al., 2019). This indicates that the value of Q will be a minimal number, either positive or negative, just to the left and right of the zero that denotes the function Q(x), respectively. In the immediate area to the left and right of that point, the value of R(x) will primarily take the form of a negative and positive number, respectively.
Oblique Asymptotes
If the function R(x) can be expressed in the form 
, then it will have an oblique asymptote. When Q(x) ≫ 0, R(x) ≈ T (x). Consequently, the curve or line denoted by T(x) transforms into an oblique asymptote. To quote an example, let us take R(x) =
. In this instance, the degree of P(x) is higher than that of Q (x) (D’Hoker et al., 2019). Therefore, there can’t be a horizontal asymptote. However, there will be an asymptote in the vertical direction when x equals -1. This is because the point in question is the zero of the polynomial in the question’s denominator.
Conclusion
As a rule, rational functions and the graphs representing them take one of three asymptotes: horizontal, vertical, or oblique. The value of the denominator determines the difference between both asymptotes, as was pointed out in this discussion. Due to these distinctions, rational functions are in a position to adequately describe the relationship that exists between velocity, range, and time. Therefore, rational functions and graphs are crucial mathematically and in real-life situations.
References
D’Hoker, E., Green, M. B., & Pioline, B. (2019). Asymptotic of the D8R4 genus-two string invariant. Communications in Number Theory and Physics, 13(2), 351–462. Web.
Lokot, T., Abramov, O., & Mehler, A. (2021). On the asymptotic behavior of the average geodesic distance L and the compactness CB of simple connected undirected graphs whose order approaches infinity. PLOS ONE, 16(11). Web.
Peraro, T. (2019). FiniteFlow: Multivariate functional reconstruction using finite fields and dataflow graphs. Journal of High Energy Physics, 2019(7). Web.