When planning to conduct a scientific study, it is important to calculate the sample size. From a practical perspective, it is not economical to study all members of a population. Thus, only a few participants are chosen. Although a smaller number in comparison with the population typifies the sample size, it is utilized to represent the whole populace. Thus, a population can be defined as a complete set of elements or participants from which a few can be included in a study sample. An important aspect to realize is that the findings obtained from a sample can be used to make conclusions about the whole populace.
The formula that is applied in determining sample size (n) does not involve the population size (N). The observation is true in the context of statistics, but it is not true from a business point of view. The formula is as follows:
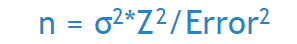
Where:
- n- Sample size in a study
- σ2– Variance of the population
- Z2– Variance/Error2
- Error2– Square of error
In the above formula, the term population size (N) does not appear. It is apparent that N could have an impact on the sample size by influencing other terms in the formula. The first term that is affected by the population size is the variance, which is used to imply the extent to which data elements of a sample are spread out in a distribution. Relatively small values of variance indicate that data in a sample distribution are close to the anticipated mean. On the other hand, relatively high values of the variance imply that data are spread out, i.e., they are not close to the expected sample mean. Large populations lead to small variances, while small populations result in high variances. Thus, it would be important for business researchers to consider the size of the populace because it would affect the distribution of data elements in relation to the expected mean. For example, populace sizes of 14 million and 20 million households would give different variances, which would impact the sample mean and conclusions about the population. In fact, the populace size of 14 million households would lead to a bigger variance than would be obtained from the populace size of 20 million households.
The square of error (Error2) in the formula would also be impacted by the populace size (N). In many studies, scientists expect some deviations (errors), which can negatively impact the study findings if they are not controlled. It is worth to note that errors can be accepted to some extent, beyond which they make the study results unreliable and invalid. From a practical perspective, the populace size positively correlates with the square of errors. Thus, small populations are associated with relatively large errors, while large populations are associated with relatively small errors that greatly improve the reliability levels of the findings. For example, a population size of 20 million households would have a smaller error than a populace size of 14 million households.
Therefore, it appears that researchers in the field of business should aim at using large populations from which they would select samples. Large populations should give rise to large sample sizes and vice-versa. From a marketing point of view, it is important to use large populations to minimize the chances of making errors that would lead to wrong conclusions about dynamics in the market.