Statistical Analysis and Linear Forecasting of Manchester City Humidity Data in April 2023 Report

Introduction

Manchester City has wet weather in April. This month’s weather is relatively chilly, but it may be tolerated with warm clothing (weather25.com, 2023). The mercury can reach 13°C. 6°C is the seasonal minimum. Consequently, Manchester’s average April temperature is 9°C. With a complete record of 24°C in 2018 and a low record of -4°C in 2013, it is essential to note that seasonal normalcy differs from that seen in Manchester in April.

Table 1: Humidity data of Manchester city from 1st April 2023 to 10th April 2023

Data Presentation

The figures below represent line and bar charts for the dataset in Table 1.

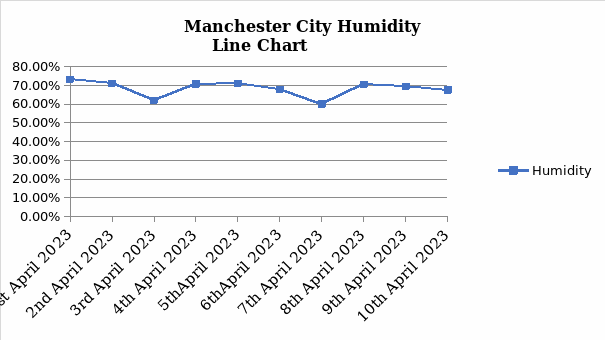
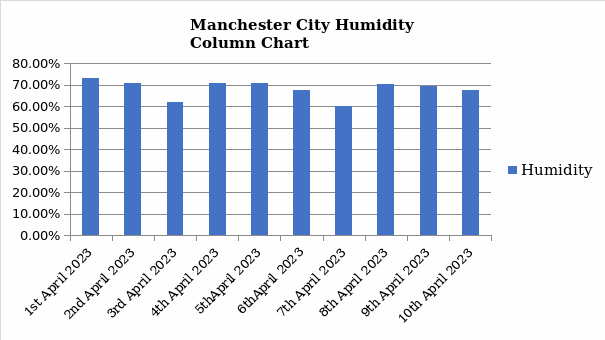
Calculations and Discussions

Mean

According to Bhandari (2020), the sum of all values of a dataset divided by the total number of values determines its mean. It is the most widely applied central tendency measure and is frequently called the “average.” Therefore, the mean April 1st to 10th 2023 humidity will be calculated as follows: (73.3+71.0+62.0+70.8+71.0+67.8+60.0+70.5+69.5+67.5)/10, which is equal to 68.34%.

Median

The steps below can be used to determine the median of a set of numbers:

1. Place the numbers in ascending order as the first step. The values are as follows: 73.3, 71.0, 62.0, 70.8, 71.0, 67.8, 60.0, 70.5, 69.5, and 67.5. The results are 60.0, 62.0, 67.5, 67.8, 69.5, 70.5, 70.8, 71.0, 71.0, and 73.3 when arranged in ascending order.
2. Find the middle number in the order. The median is the middle number when there is an odd number of elements in the set of numbers (CueMath, n.d.). Since the collection contains ten numbers, the median will be the average of the two middle integers. 69.5 and 70.5 are the numbers in the center. Taking the average of the two middle values determines the median. Thus, the median is (70.0) = (69.5 + 70.5) / 2. The given set of numbers’ median is 70.0%.

Mode

The number that appears in the set most frequently is the mode, according to CueMath (n.d). This may be determined by doing the following steps: The numbers are 73.3, 71.0, 62.0, 70.8, 71.0, 67.8, 60.0, 70.5, 69.5, and 67.5. The numbers 71.0 and 67.5 appear twice, making them both the set’s modes. Therefore, 71.0 and 67.5 represent the mode of the provided numbers collection.

Range

These steps should be followed to determine the range of a set of numbers, which is the difference between the highest and lowest values in the set.

1. Find the highest and lowest values as a first step. From the values in Figure 1 above, 73.3 is the greatest value, and 60.0 is the lowest.
2. The range in this scenario can be estimated as follows: 73.3% – 60.0% which is equal to 13.3%.

Standard Deviation

The standard deviation of a set of numbers can be calculated as follows.

1. The first step is to find the mean (average) of the numbers (Math Is Fun, 2017). In this case, the set of data in Figure 1, the mean, is equal to 68.34%.
2. Subtract the mean from each number and square the result. This is achieved.
   (73.3 – 68.34)² = 24.6016,
   (71.0 – 68.34)² = 7.0756,
   (62.0 – 68.34)² = 40.1956,
   (70.8 – 68.34)² = 6.0516,
   (71.0 – 68.34)² = 7.0756,
   (67.8 – 68.34)² = 0.2916,
   (60.0 – 68.34)² = 69.5556,
   (70.5 – 68.34)² = 4.6656,
   (69.5 – 68.34)² = 1.3456, and
   (67.5 – 68.34)² =0.7056.
3. Then (24.6016+7.0756+40.1956+6.0516+7.0756+0.2916+69.5556+4.6656+1.3456+0.7056)/10, which is equal to 16.1564.
4. Take the square root of the result, which is the standard deviation. The √(16.1564) is 4.0195024567724 ≈ 4.0195.

Forecasting

Use the linear forecasting model, which is y = mx + c, to calculate and discuss the following:

Calculating the m Value

Using data in Table 1, the mean (average) of the x and y values is calculated. In this instance, the day numbers (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) would be represented by the x–values, and the y-values would represent the humidity values, which are 73.3, 71.0, 62.0, 70.8, 71.0, 67.8, 60.0, 70.5, 69.5, 67.5. The mean for x-values (day numbers) is equal to 5.5. The y-values (humidity): 68.34 is the average for y.

The slope (m) of the linear forecasting model must then be calculated. The formula that can be used to do this is m = ((x_i – x)(y_i – x)) / ((x_i – x)²). where x_i is each x-value, x is the average of all x-values, y_i is each y-value, and y is the average of all y-values (Atmos.washington.edu, n.d.) Plugging in the values, we get:

m = ((-22.32)+(-9.31)+(15.85)+(-3.69)+(-1.33)+(-0.27)+(-12.51)+(5.4)+(4.06)+(-3.78)) / ((-4.52)+(-3.52)+(-2.52)+(-1.52)+(-0.52)+(0.52)+(1.52)+(2.52)+(3.52)+(4.52)).

After calculating the above expression, m = ((-27.9)/82.5) = -0.338181818181 ≈ -0.3382(4 decimal places). The slope (m) value is -0.3382.

Calculating the c Value

The previously estimated mean for x is 5.5. Mean of y = 68.34 (already computed). The y-intercept (c) in the linear forecasting model is determined using the following formula: c = – m * x, where is the mean of the y-values, m is the slope (already obtained), and x is the mean of the x-values. With the data entered, c = 68.34 – (-0.3382) * 5.5. After calculating the previously stated expression, c = 70.2001 ≈ 70.2.

Forecasting Humidity on Day 12 and Day 13

Day 12: x = 12 m = -0.3382 (already computed); c = 70.2 (previously calculated). The result is: y = (-0.3382 * 12) + 70.2. y = 66.1416 ≈ 66.14%.

Day 13: x = 13 m = -0.3382; c = 70.2. The result is: y = (-0.3382 * 13) + 70.2. y = 65.8034 ≈ 65.80 %.

Conclusion

The examination of Manchester City’s humidity data over ten consecutive days shows essential information regarding the city’s humidity levels. To highlight the patterns and comparisons, the data was sorted in a table style and visualized using line and bar charts. The statistical measurements that have been calculated, including mean, median, mode, range, and standard deviation, provide us with a thorough comprehension of the humidity data. These measurements aid in determining the average, range, and distribution of humidity levels over 10 days in Manchester City.

References

Atmos.washington.edu. (n.d.). Linear Regression. Web.

Bhandari, P. (2020). The Mean | What It Is and How to Find It. Web.

Math Is Fun (2017). Standard Deviation Formulas. Web.

CueMath (n.d.). Mean Median Mode – Definition, Formula & Solved Examples. Web.

Weather25. (2023). Manchester Historical Past Weather. Web.