Introduction
This paper aims to analyze various attributes that influence movie likes on Facebook as a measure of its market reach, factors that may serve as predictors of IMDb movie ratings, and the variations in these likes by demographic characteristics using appropriate statistical techniques. Before presenting the analyses, a methodology is presented that describes the merits and pitfalls of the statistical techniques. The report later presents a descriptive analysis of the variables of interest and a statistical analysis of the selected variables relating to movie likes on Facebook and movie ratings. The study then highlights variables that show a significant relationship with IMDb movie likes and those that explain variations in IMDb movie ratings. The analysis offers recommendations to movie management regarding the IMDb rating score and Facebook reach, based on the results obtained.
Methodology
This analysis employed various statistical techniques to identify and reveal the factors influencing IMDb movie likes on Facebook and their corresponding ratings. ‘IMDb movie likes on Facebook’ Variable is a continuous or scale variable; thus, analysis of variance, Pearson Correlation, and t-tests have been deployed to analyze its association with other categorical and scale variables such as the number of actors’ likes on Facebook, duration, number of critics for reviews, and aspect ratio (Cronk 2017).
When Pearson correlation is used, it reveals the magnitude and direction of the relationship between two variables, but does not indicate the marginal change or causality between them. This would suffice to understand variations in the IMDb scores by groups. However, the Pearson correlation requires that the two variables have a normal distribution to ensure accuracy and reliability.
On the other hand, analysis of variance compares the distributions of more than two groups, assuming normal distributions and equal variances, to determine whether the population means are equal. The ANOVA provides group means and between-groups analysis. However, it may not be reliable when the data do not follow a normal distribution. Linear regression shows an association with causality between an outcome variable and at least one predictor using ordinary least squares estimation.
In linear regression, the marginal effect of each variable on the outcome. However, the marginal effects may suffer setbacks when there are omitted variables and misspecification biases. The independent samples t-test, as described by Cronk (2017), compares two population distributions to determine whether there is a statistically significant difference in their means. This technique assumes a normal data distribution for reliability, but may be substituted with the Mann-Whitney U test when the data has a non-normal distribution.
The IMDb review is a continuous variable, and the factors influencing it will be analyzed using the same statistical techniques as those mentioned in the above paragraph. These techniques include independent samples t-test, One-Way analysis of variance, linear regression, and Pearson correlation, among others. When the data show a non-Gaussian distribution, correction techniques will be applied to ensure the reliability of the parametric tests (Cronk 2017).
Furthermore, the analysis will examine the presence of outliers to account for the impact of large, exceptional values. The data sample size provided here is sufficiently large (n = 5043); it is assumed that the statistical methods are reliable, although some may have limitations as described in the text.
Analysis
Table 1: Descriptive statistics
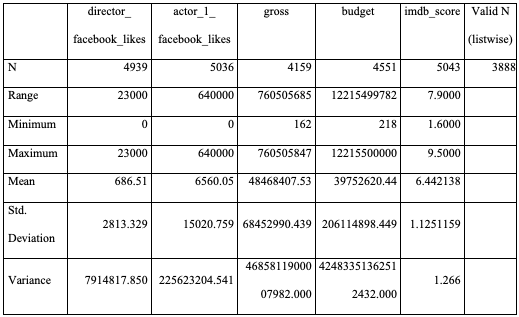
The table above presents descriptive statistics of variables that influence the profit generated by a given movie. These variables include director and actor 1 Facebook likes, and IMDb score. The genre of the movie has not been included because a single movie may encompass multiple genres, including Action, fantasy, drama, romance, and adventure.
The variable ‘Facebook likes’ has a mean of 686.51; the maximum number of likes for directors is 23000, and the minimum is 0. Actor 1 Facebook likes have a mean of 6560.05, a maximum of 64,000, and a minimum of 0. IMDb score has a mean of 6.44, with a maximum of 9.50 and a minimum of 1.60. Variables exhibit a large variation, as indicated by their variance and standard deviation, implying that the data is dispersed.
Factors Affecting Pre-Production
Hypothesis 1
The current study examines the relationship between variables, including the popularity of the director and that of actor 1. The Brand theory states that the effects of the brand are generated from the audience’s knowledge. It suggests that the popularity of actors and directors has a significant impact on film consumption (Gaenssle et al., 2018). The audience develops perception, knowledge, and experience using the popularity of actors and directors.
Gaenssle, Budzinski, and Astakhova (2018) argue that a popular director or actor has a significant impact on box office performance. This is because they help reduce the insecurity the audience faces regarding the movie, attracting consumers who want to see more from the actor or director.
They have a crucial role in risk aversion during the pre-production process. This makes it essential to determine the movie’s budget. According to a study by Almaganbetov (2018), the actor’s popularity has a significant impact on the box office’s success. It is crucial for the company producing the movie brand to assess the impact of the actor and director before investing in a particular movie. Linear regression is used to examine the effect of the director’s Facebook likes and the actor’s Facebook likes on the profits generated.
Table 2: Regression analysis of popularity and actor 1 Facebook likes
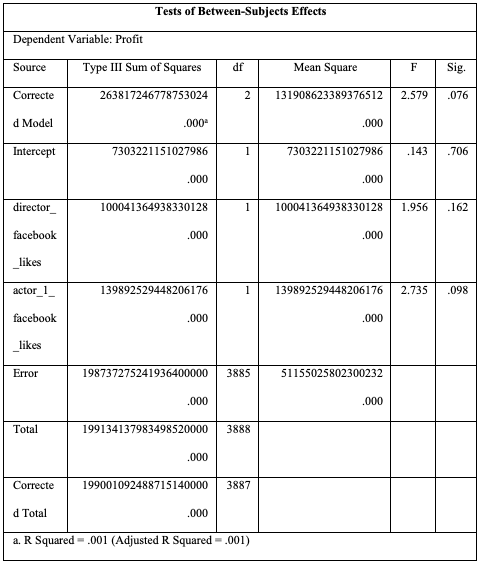
The table above shows the p-value of 0.076, which is greater than the standard p-value of 0.05. This implies that the director’s Facebook likes and the actors’ likes are not significant in predicting the movie’s profit. Additionally, it does not have a significant impact during pre-production. This analysis’s findings contradict the findings of Gaenssle, Budzinski, and Astakhova (2018) and Almaganbetov (2018).
Also, based on the multiple R-squared values, it can be concluded that 0.1% of the variation in the profit generated from the movie can be explained by the combined variation of the director’s Facebook likes and the actor’s 1 Facebook likes. This finding is similar when using the adjusted R-squared, which takes into account the sample size.
Hypothesis 2
Technological advancements have enabled movies to achieve high resolution and utilize a wider range of colors. Currently, most movies use multiple colors; however, this does not imply that there are no black-and-white movies. Color has been favored by the movie industry as its appearance has evolved. Despite these changes, studies have not focused on the color of the movies affecting the pre-production process, which later affects the profit generated. This study evaluates the relationship between color and the movie’s profit using an independent t-test.
Table 3: Independent t-test
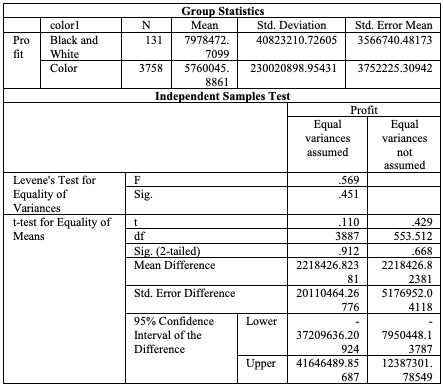
The analysis Table 3 shows that the p-value of Levene’s test is 0.45, which is greater than 0.05. This implies that the null hypothesis that movie color does not affect profit is not rejected. It shows that the movie’s black and white and color do not necessarily impact the profit generated from it. Although the color is a significant aspect of a movie, its effect on affecting profit generated is not high, considering that black and white movies have a higher mean than color movies.
Factors Affecting Post Production
Hypothesis 3
Table 4 below shows that all the records used to find the relationship between content rating and the gross new tab are included in the analysis. R has the highest content rating, with a total of 2,118 ratings. It is followed by PG-13 with a content rating of 1461. The third content rating is PG and has a content rating of 701. The Pearson chi-square value in Table 5 is less than 0.001, implying a significant relationship between the gross new tab and content rating.
Table 4: Cross Tabulation
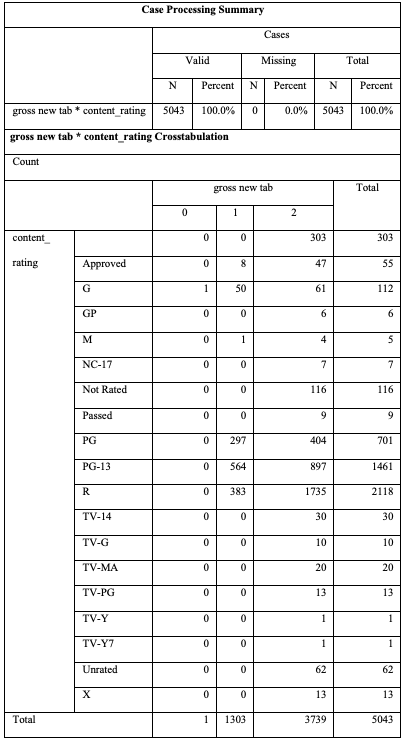
Table 5: Chi-square tests
Hypothesis 4
The IMDb score influences the dissemination of information about a particular movie. Movies with high IMDb scores spread rapidly on the internet through social media, increasing their popularity and gross revenue (Johansson, 2020). Information about the movie spreads quickly among consumers, as many people will want to watch movies with high scores. This is because the score is generated by other consumers who may have a similar perception of the movie.
Table 6: Regression IMDb Score and revenue
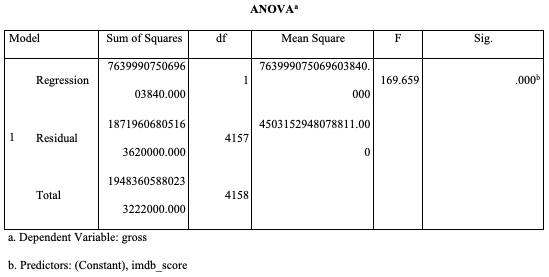
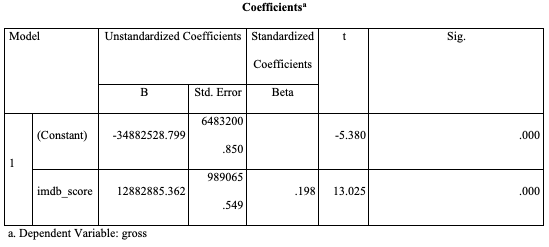
The analysis in Table 6 indicates that the IMDb rating has a significant impact on the movie’s revenue generation. This is because the p-value of the linear regression is less than 0.01, thereby rejecting the null hypothesis that the IMDb rating has no significant effect on the revenue generated from the movie. The R-squared value is 0.039, implying that 3.9% of the variation in revenue generation is explained by the IMDb ratings. Although the R-square is not strong, it provides critical information on the revenue predictor. Considering the sample size, the adjusted R-squared value is also 0.039.
Hypothesis 5
Actors have different preferences on their social media accounts, which may impact the movie’s revenue depending on the type of actor consumers want to follow or view their content. Some actors are rated higher than others based on Facebook likes, resulting in differences in the effect they have on the audience. Focusing on the popularity of the director, along with the acclaim received by actors, may help develop a model that identifies the types of actors capable of driving high revenue generation in the movie industry.
Table 7: Regression popularity of the director and actors’ Facebook likes
Tests of Between-Subjects Effects
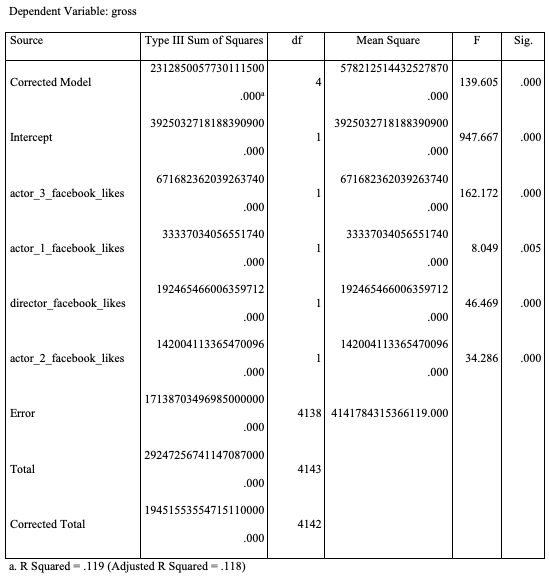
The p-value from the analysis in Table 7 is less than 0.01, indicating that the null hypothesis—that the popularity of the director and actors, based on Facebook likes, does not affect the revenue generated from the movie—is rejected. The R-squared value is 0.119, implying that 11.9% of the variation in revenue generated from the movie is explained by the variation in director, actor 1, actor 2, and actor 3’s Facebook likes.
Summary and Recommendations
The current study analyzed several factors influencing a movie’s profit and revenue, including the popularity of the director, lead actor, supporting actors, and IMDb score. While previous research (Gaenssle, Budzinski, & Astakhova, 2018; Almaganbetov, 2018) claimed that director and actor popularity significantly boosts box office performance by attracting audiences, this study found that their popularity may not have a significant effect on profit, although it is crucial for driving revenue. Finally, the analysis also showed that despite technological advances, a movie’s color scheme (colored versus black and white) does not create a significant difference in profit generation.
The study reveals that the content rating of a movie influences its genre. The IMDb score has been found to have an impact on either promoting or demoting a movie’s revenue. Johansson (2020) argues that the IMDb score is critical in determining gross earnings. Movies with high IMDb scores attract many viewers, as the audience often shares this information through social media, thereby promoting them.
The study recommends that when preparing for a movie, it is essential to consider the director’s popularity and that of other actors. This will help reduce the risks associated with the movie, as the audience tends to prefer content from people they are familiar with. The production should not focus mainly on one popular actor to promote the movie’s views.
Reference List
Almaganbetov, A. (2018). The effect of star power on movie success: Evidence from the Kazakh cinema industry. Thesis. Web.
Cronk, B.C. (2017). How to use SPSS®: A step-by-step guide to analysis and interpretation. Routledge.
Gaenssle, S., Budzinski, O., and Astakhova, D. (2018). ‘Conquering the Box Office: Factors influencing Success of International Movies in Russia’, 24(113), pp. 1–16. Web.
Johansson, J. (2020). The box office before and after streaming services. Thesis. Web.