Introduction
When making decisions, performing statistical quantitative data analysis is often a good practice. This approach minimizes data bias and justifies conclusions based on statistics. Statistical analysis applications are broad and include, but are not limited to, sociology, politics, business, and management (Adams & McGuire, 2022).
This paper uses descriptive statistical analysis to examine data from a survey of 445 respondents from New York City. Respondents from a random sample were surveyed about their general attitudes toward a particular neighborhood in the state, whether Manhattan, Brooklyn, Queens, The Bronx, or Staten Island. In addition, respondents were also asked about their highest level of education and family status. This paper aims to conduct a statistical analysis of the data collected and draw conclusions based on the findings.
General Attitudes Towards Boroughs
Data on general attitudes toward a particular area of the state were collected on an ordinal five-point Likert scale, where “1” corresponds to the lowest degree of attractiveness of the region to the respondent and “5” to the highest level. To calculate the mean, a descriptive analysis was conducted for each of the five areas, and 95% confidence intervals were constructed (Hespanhol et al., 2019).
Table 1 shows the results of calculations of mean values and standard deviations for each of the five regions, and Equations [1] and [2] show examples of calculations for Manhattan.
Table 1. Respondents’ overall mean attitudes toward each of the boroughs
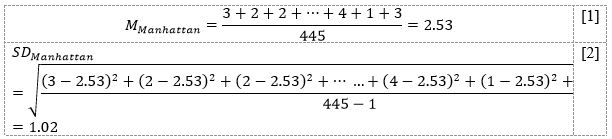
Manhattan
The formula in equation [3] must be used to construct the 95% confidence interval. With a 5% chance of being wrong, the z-score is 1.96. Since all values are already known, simply substituting them into Equation [4] allows us to find the population mean confidence interval bounds of people’s overall attitude toward the Manhattan area, as shown in Equation [4].
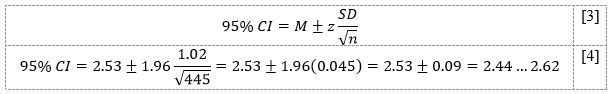
This indicates that with 95% probability, one can be confident that the true population mean of people’s attitudes toward the Manhattan region is between 2.44 and 2.62, indicating an estimate between “Dislike” and “Neutral.”
Brooklyn
The same procedures were followed for the Brooklyn area: equation [5] displays the findings of the 95% confidence interval computations. The true population mean of individuals’ opinions about the Brooklyn area is, therefore, between 4.58 and 4.74 with 95% confidence, which indicates an estimate between “Like” and “Like Very Much.”

Queens
Similar steps were performed for the Queens region: equation [6] shows the results of the 95% confidence interval calculations. Thus, with 95% confidence, the true population mean of people’s attitudes toward the Queens region is between 2.64 and 2.88, indicating an estimate between “Dislike” and “Neutral.”

The Bronx
The Bronx region underwent similar procedures; the results of 95% confidence interval computations are displayed in equation [7]. The true population mean of opinions about the Bronx region, then, is between 2.30 and 2.58 with 95% confidence, which is an estimate between “Dislike” and “Neutral.”

Staten Island
Lastly, comparable procedures were carried out for the Staten Island region: the 95% confidence interval computations’ outcomes are shown in equation [8]. The true population mean of people’s impressions of the Staten Island region is, therefore, between 3.74 and 4.02 with 95% confidence, which indicates an estimate between “Neutral” and “Like.”

Educational Status
Also of interest was a study of the 95% confidence interval for the proportion of people in the sample with a doctoral degree. The data were distributed on an ordinal six-point scale, and the doctoral degree corresponded to a value of “6.”

The calculated proportion (equation [9]), standard deviation (equation [10]), and confidence interval (equation [11]) were calculated. From this, it follows that with 95% probability, one can be confident that the average proportion of people with a doctoral degree is between 3.4% and 7.8%.
Family Status
Similar procedures to equations [9]-[11] were performed for the marital status of respondents with the “single or other” category. Equations [12]-[14] show a 95% probability that the true proportion of people in the population who are single or unmarried is between 77.8% and 84.8%.

Determination of Sample Size
The calculations of mean values and confidence intervals are sensitive to sample sizes, so appropriate sample sizes must be calculated according to equation [15]. Equations [16]-[20] show the results of sample size calculations for each region.

Conclusion
The current study concentrated on using statistical analyses to calculate sample sizes, mean values, and confidence intervals from the survey data that was gathered. The findings calculate the percentages of individuals with a doctorate and those who are single or unmarried, as well as the general population ratio, with a 95% probability for each of the state’s five areas. Furthermore, sample sizes were determined to be adequate to incur an error of 5% or less for each location. The outcomes of the analysis are presented in the article, which could help with future decision-making.
References
Adams, K. A., & McGuire, E. K. (2022). Research methods, statistics, and applications. Sage Publications.
Hespanhol, L., Vallio, C. S., Costa, L. M., & Saragiotto, B. T. (2019). Understanding and interpreting confidence and credible intervals around effect estimates. Brazilian Journal of Physical Therapy, 23(4), 290-301. Web.