Abstract
A gas is one of the three states of matter whose particles are separated by vast distances, which allows gases to be compressible. A number of laws have been devised to explain the behavior of gases under various environmental conditions, such as temperature and pressure. Charles’ law describes the behavior of gases when subjected to changing volumes and temperatures at an invariable pressure.
On the other hand, Boyle’s law illustrates how gases behave at changing pressures and volumes at even temperatures. This experiment intended to verify these two gas laws using air. It is also set to establish the value of the absolute zero temperature and compare it to the literature values. It was observed that the gas samples obeyed the two gas laws. However, there were variations in the literature values of the absolute zero temperature and the documented literature values because of experimental errors. It was concluded that, with increased accuracy, simple laboratory procedures could be used to very gas laws.
Introduction
Matter exists in three different forms. These three distinct forms are solid, liquid and gas. Gas is the state of matter where particles (molecules or atoms) have the largest space separating them. Gases also have the ability to contract and expand easily and, therefore, do not have clear-cut shapes or volumes. The vast distances between the particles that make up gases give gases the property of compressibility. Various theories attempt to explain the properties of gases. The kinetic theory of matter, for example, tries to explain the behavior of gases based on the nature of the associations among the particles that make up a gas. In the eighteenth century, scientists realized that almost all gases behaved in a similar manner when subjected to certain conditions such as temperature and pressure. That behavior was attributed to the fact that all gases had widely-spaced molecules.
An investigation by Boyle realized that subjecting a gas to varying amounts of pressure at the same temperature caused the gas to reduce in such a manner that the product of the gas volume and the pressure did not change. That discovery came to be referred to as Boyle’s law, which is still in use to date. An equation that describes Boyle’s Law is written as P×V=k where P is the gas pressure, V is the volume of gas and k is a constant.
Charles, a different scientist, also realized that reducing the temperature of a gas while maintaining the same temperature caused the volume of the gas to reduce in size at a steady rate. Charles’s law is depicted by the equation V/T = k where V is the gas volume, T is the gas temperature and k is a constant.
It was realized that decreasing the temperature of a gas while compressing it enabled a gas to be compressed for an indefinite period. Hypothetically, it was thought that it was possible to compress a gas until its volume reached zero. The temperature at which the gas attained a volume of zero was what was referred to as the absolute zero of temperature. The absolute zero was equivalent to -273 oC or -469.67 oF. It was suggested that a thermodynamic system possessed the minimum energy at that temperature.
This experiment aimed at verifying Charles’s law and Boyle’s Law on air, which is a blend of different gases. It also aimed at estimating the value of the absolute zero by extrapolating the plot of volume versus temperature.
Experimental Procedure
Charles’s Law
A glycerin plug whose length was about 2 to 3 cm was inserted a third of the way into a blood serum sample tube, which acted as the gas law tube, with the aid of a long disposable pipette (Grossie and Underwood 109). The volumes of the gas column in the sample tube were established at four different temperature conditions. The volumes were determined starting from the lowest temperature (oC) to the highest temperature by putting a thermometer adjacent to the gas tube in different water-baths at steady temperatures. The gas volumes were read from the markings on the capillary tube within two to three seconds of placing the tube in the water-baths.
The first water-bath was a beaker that contained ice at a temperature of 0oC. The second condition was room temperature air, whereas the third condition was warm water at temperatures between 60 and 70 oC (Grossie and Underwood 108). The fourth condition consisted of hot water at a temperature of 85oC. Boiling chips were added to the beaker with hot water. The water-baths comprised a total volume of 150 ml, and the temperatures were maintained at the required levels by cooling or heating as was required. It was ensured that the tube did stay in the water-bath for longer than was necessary.
The temperatures at the different conditions were recorded and well as the corresponding gas heights. Subsequently, a plot of length (cm) against temperature (oC) was made. The plot was extrapolated to determine the absolute zero value in oC. That value was later converted to degrees Fahrenheit. The quotient of volume divided by temperature was computed for each of the points. That value was used to determine whether Charles’s law had been verified.
Boyle’s Law
A burette and reservoir were arranged in order to establish the association between the volume and pressure of a gas. An air sample was confined in the burette after which the pressure acting on the gas was adjusted by altering the height of the connected reservoir. The apparatus was filled by opening the stop clock in such a manner that the burette was roughly half-full when the reservoir was close to the burette’s endpoint. The top of the burette was corked to trap the air at atmospheric pressure. The levels of water in the burette and reservoir were quantified and put into a table. The volume corresponded to the height of the gas in the burette, whereas the pressure of the gas corresponded to the variation between the two levels of water. The atmospheric pressure was obtained and recorded in a table.
The reservoir was shifted to different levels that were higher than and lower than the starting point to obtain varying pressures. The pressure of the gas (P gas) and volume of the gas (V gas) were computed and recorded. A plot of P gas versus the reciprocal of gas volume (1/V gas) was made and used to verify Boyle’s Law.
Data and Results
Charles’s Law
Table 1: Charles’ Law.
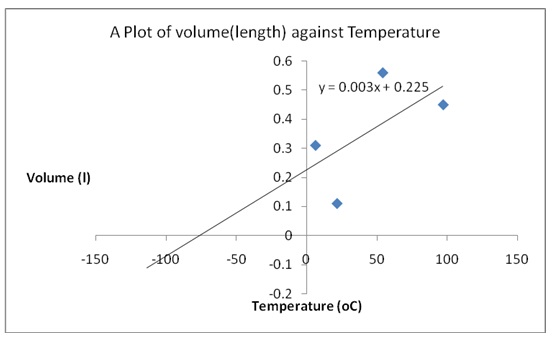
Plot of Volume versus Temperature
Calculated Quotient of V/T
Table 2: The computed quotients of volume and temperature.
Absolute Zero Determination in °C and °F.
The absolute zero was obtained as -75oC from extrapolation of the plot in figure 1. The equation of the line was y=0.003x+0.225. Therefore, substituting y with 0 (when V =0) gave -75 oC, which was converted to oF as follows.
oF= 9/5 (-75) +32 =-103oF.
Boyle’s Law
Table 3: Boyle’s Law.
Calculated Product of PV
Table 4: The calculated products of volume and pressure.
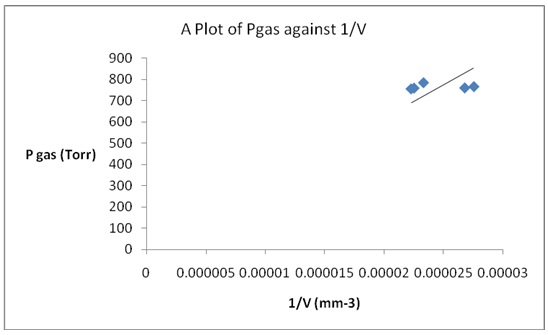
Plot of Pressure versus Inverse of Volume
Discussion
There were significant differences in the quotients of V/T especially in the value that was obtained at room temperature. Those differences indicated that Charles’s law did not hold for the sample gas at that temperature. However, the quotients obtained at 0oC (in an ice-bath) and in hot water (at 97.0 oC) did not exhibit significant variability. That observation showed that, at those two temperatures, Charles’s law applied to the behavior of the gases. The reason for that occurrence was that there were high chances that the procedures and measurements at those temperatures were taken with high precision. It was likely that the sample tube was allowed to stay in the water baths at the appropriate length of time. Therefore, there was no overheating of the gas in the tube that would cause it to expand more than was necessary.
There were no significant variations in the values of the products of pressure and volume. That was because Boyle’s law applied to the gas at the experimental temperature. From Boyle’s equation, it was known that the product of pressure and volume was consistent. Therefore, the constancy of the P×V values indicated that Boyle’s law was confirmed.
Charles’s law was verified because a straight line graph was obtained. The straight line indicated that indeed gas volume increased steadily with an increase in temperature was constant at a constant pressure. In addition, Boyle’s law was also verified because a straight-line plot was obtained when pressure was plotted against the reciprocal of volume. The straight line revealed that there was an inverse association between pressure and the volume of a gas.
The absolute zero value that was obtained from the experiment was -75oC or -103 oF. The experimental values differed from the literature values of 273 oC or -469.67 oF. Various experimental errors probably altered the accuracy of the results.
Although Charles’s law and Boyle’s law were confirmed, there were variations in the quotients of V/T and the products of P×V. Those variations were consequences of experimental errors. The quotient obtained at room temperature was substantially small because it was likely that room temperature was not constant. Factors such as a sudden wind could have blown thereby affecting the temperatures of the water-baths and the subsequent readings. It was also possible that the graduations on the apparatus were not read accurately. In addition, it was noted that the value of absolute zero obtained was not as exactly as it was in the literature. The above mentioned experimental errors played a significant role in the difference between literature values and experimental values of the absolute zero temperature.
References
Grossie, A David and Kirby Underwood. Laboratory Guide for Chemistry. 6th ed. 2012. Plymouth, MI: Hayden-McNeil. Print.