The Central Limit Theorem and Its Applications Essay

Introduction

One of the critical areas of mathematics used for both routine and academic purposes is statistics. Strictly speaking, statistics is a mathematical discipline that studies the ability to analyze and interpret data, whether numbers or categories. In statistics, or more specifically, probability theory, a fundamental concept called the Central Limit Theorem (CLT) is of great importance. The present expository essay will focus on a comprehensive study of the CLT phenomenon and on finding applications of this concept to life.

Central Limit Theorem

It is paramount to emphasize that statistical researchers do not have the practical ability to conduct an experiment on an entire population. For example, if the topic of the paper is to evaluate the potential association between an individual’s height and income size, it is physically impossible to involve the population of a community; instead, a sample must be used. The sample must be representative enough to reflect the characteristics of such a population, but the sample will never be completely identical. In other words, the need to use smaller sample sizes will always lead to systematic errors that can affect the reliability of the results.

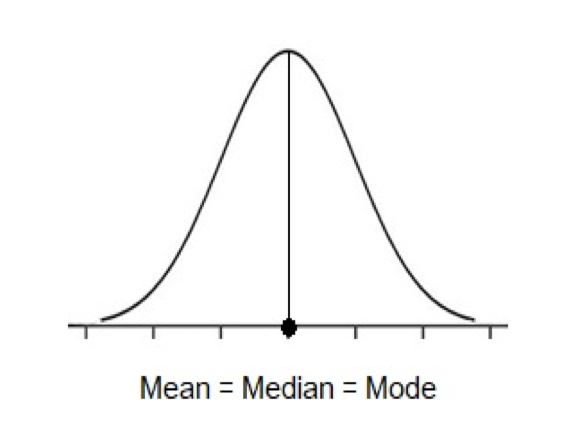
The CLT is a universal tool that allows covering this problem. A basic formulation of the CLT might be “the theorem that specifies the nature of the sampling distribution of means according to the central tendency, the variability, and the shape of the distribution” (Barri 592). In simple words, this means that as the sample size increases, any variable’s distribution begins to be normal. It is worth saying that a normal or Gaussian distribution is a bell-shaped curve distribution of a variable for which the median, mode, and mean are identical, as shown in Figure 1. The CLT postulates that a robust distribution of growth and income measures of a sample will be achieved when the sample size tends to be the maximum. Thus, measurements for 10, 100, and 1,000 respondents will increase the statistical reliability of the results, respectively.

It is clear that the CLT has been proved from a mathematical perspective, which means that there is a formulaic notation for this statement. Indeed, a reference to the equation below shows the relationship underlying the CLT (OpenStax). This notation shows the distribution of a random variable X, such as growth, the population means μ_x, and the standard deviation σ_x — they are the essential tools of descriptive statistical analysis. The formula perfectly shows that increasing the sample size n will have an effect on the distribution of the random variable.

However, there is an alternative notation that means the same. In particular, as shown in the equation below, the distribution of the sample mean converges to the distribution of the general population when tending to infinity (Glen). This means that the sample means will always be equal to the population means in light of the CLT — this is an extremely important assumption that optimizes most quantitative studies.

In real life, the CLT is used primarily in research projects that use data collection procedures. A minimum of thirty measurements is thought to be necessary to cover the minimum CLT threshold, and thus any smaller sample size should be considered unreasonable (Ganti). On the other hand, the theorem should always be kept in mind when conducting life experiments. For example, if the result of a decision coin flip turns out to be the same several times, this does not mean — though it may — that the game is unfair but rather hints at the need for more measurements to reach the true mean, which is 0.50. Since the CLT ensures that experimental results are most accurate when the sample size is expanded, this accuracy is used for pharmacological, manufacturing, and sociological studies.

Conclusion

In conclusion, it is worth emphasizing that the CLT is an important mathematical tool to simplify statistical analysis. The CLT eliminates the need to know the population means because the sample value will be the same. This creates room for using the CLT in practice in order to better understand the nature of phenomena and processes at a lower cost.

Works Cited

Barri, Moatasim A. “A simulation showing the role of the central limit theorem in handling non-normal distributions.” American Journal of Educational Research, vol. 7, no. 8, 2019, pp. 591-598.

Ganti, Akhilesh. “Central Limit Theorem (CLT).”Investopedia, 2022.

Glen, Stephanie. “Central Limit Theorem: Definition and Examples.”Statistics How To.

OpenStax. “The Central Limit Theorem for Sample Means (Averages).”LibreTexts, 2021.