Time series is instrumental in tracking variables over time because they can be decomposed into four distinct components: trend, cycle, seasonal, and irregular. This decomposition helps analysts evaluate performance and make predictions by isolating the underlying drivers of the time series data. Therefore, trend element signifies the long-term direction of the time series, while the cycle component represents any recurring patterns (Trampusch & Gross, 2019). The seasonal component represents regular patterns that occur at specific times of the year, and the irregular component represents any remaining variability that the other three components cannot explain.
Time series models are utilized in predicting future principles of a time series centered on earlier values. Thus, the four components of a time series comprise trend, cycle, seasonal, and irregular. The trend is the long-term movement of the data, which comprises increasing, decreasing, or stable data. The cycle captures the medium-term fluctuations. The seasonal component represents the short-term fluctuations that occur at specific times of the year. They are generated by Seasonal patterns caused by factors such as weather and holidays (Trampusch & Gross, 2019). The irregular component is the random variation in the data, which can be caused by errors in data collection or unforeseen events. The additive model is the simplest of the two-time series models. It is used when the components are not correlated with each other. In the additive model, the four components are added together: the multiplicative model is more complex. It is used when the components are correlated with each other. In the multiplicative model, the four components are multiplied together.
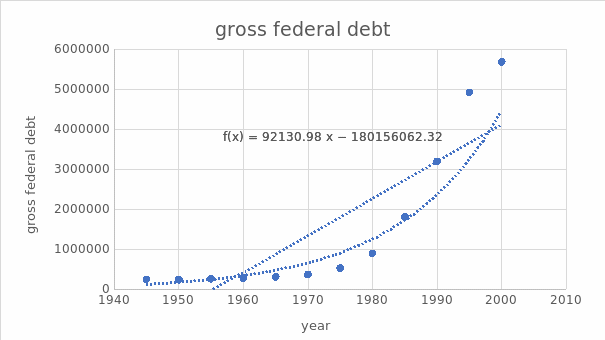
The data given to address the gross federal debt for the United States every five years was used in the chart above from 1945 to 2000 (Trampusch & Gross, 2019). The statistics in figure 1 show that the linear model seems more appropriate, as it closely resembles the data. The exponential model seems to be overfitting the data. The linear model demonstrates that the data is increasing at a constant rate. The exponential model states that the data is increasing at an increasing rate. The exponential trend appears to be more appropriate. The linear trend fits the data better in the early years, but the exponential trend appears to fit the data better later. This is likely because the number of cases is increasing exponentially, so the linear trend cannot capture this increase.
Reference
Trampusch, C., & Gross, P. (2019). Do parliaments have control over sovereign debt management? West European Politics, 44(2), 299-326.