The aim of the paper is to research the pilot project, intended to examine the duct of the rectangular section. The principle, which is used for the research is based on Bernoulli equation, which is represented in the following equation:
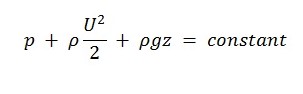
The research investigates and demonstrates the use of a pilot-static tube, and emphasized the application of Bernoulli’s theorem to flow along a convergent-divergent passage.
The aim of the experiment is to test the liquid flow in the pilot tube, with the convergent-divergent flow. The air is blown through the passage, and a Pilot-static probe is traversed along the centerline to measure the distribution of total pressure P and static pressure p. The total pressure will be counted with the following formula:
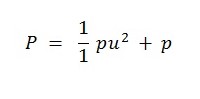
Then, the results will be compared with Bernoulli’s equation. As the variations of static pressure may be measured by the holes in the sides of the tube, it is offered that the holes will be located far from the tips of the tube, in order the results were not interfered by the disturbance of the locality of the holes. Thus, the undisturbed static pressure may be measured.
The objective of the report is to describe the experiment briefly, and give the central considerations, which were derived from the experiment, and the application of Bernoulli equation. Originally, the total pressure and the speeds of the fluid flows are counted with taking into consideration the gravity potential, while the offered experiment is arranged neglecting this potential in the total counts. Originally, it is another objective of the report – to explain whether the gravity potential will affect the results of the experiment.
The literature background of the experiment will entail the similar researchers, where pilot tubes were involved. The experiment should take into consideration the results of previous experiments, where the gravity factor was and was not taken into consideration. Consequently, it will be possible to conclude whether it is important for the present research.
In accordance with McDonald (2004), the following statement should be emphasized:
With the difference in pressures measured and knowing the local value of air density from pressure and temperature measurements, we can use Bernoulli’s equation to give us the velocity. On the graphic, the Greek symbol rho is used for the d air density. Bernoulli’s equation states that the static pressure plus one half the density times the velocity V squared is equal to the total pressure.
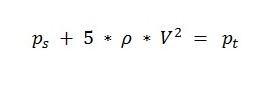
Where:
- Ps is for Static Pressure
- Pt is for total pressure.
The purpose of the experiment is associated with the concept of applying the convergent-divergent flows in liquid mechanics, aerodynamics and aviation. Originally, the results of the experiment may become the beginning of the new era of avionics, and the new generations of the airspeed tubes in planes and helicopters.
Finally, it should be emphasized that the original experiment will be arranged in accordance with the new trends of liquid mechanics, and the researches, which are held in the sphere of air dynamics.
Reference
McDonald G. S. (2004) “Bernoulli Equations” Promoting Physics Learning & Teaching Opportunities. 2004