Regression analysis is a statistical tool that is used to develop and approximate linear relationships among various variables. Regression analysis formulates an association between several variables. When coming up with the model, it is necessary to separate between dependent and independent variables. Regression models are used to predict trends of future variables (Arnold 2011). The paper carries out simple regression analysis to establish the relationship between salaries and the number of years the employees have worked in the organization. Further, scatter plots will be drawn to establish the relationship between the variables. Finally, confidence intervals will be calculated to determine the range within the average values. The analysis will be based on a sample of 135 observations.
Descriptive statistics
Table 1.0 presented below shows a summary of the descriptive statistics.
From the table presented above, the mean and median for salaries are 90.62 and 75.2 respectively. The maximum and minimum values of salaries yield a range of 519.9. The standard deviation, a measure of dispersion, for salaries is 62.57. This implies that the mean can deviate by up to 62.57. The value of skewness (3.03), Kurtosis (19.86) and Jarque Berra (1805.176) indicates that the observations are not normally distributed. In a normal distribution, the value of skewness and Kurtosis should be zero. The mean and median for the number of years they have been senior officers are 22.99 and 23 respectively. The maximum and minimum values yield a range of 45 years. The standard deviation is 11.67. The value of skewness (-0.11), Kurtosis (1.88) and Jarque Berra (7.41) indicates that the observations are not normally distributed. Finally, the mean and median for the number of years they have worked for the company are 7.8 and 6 respectively. The maximum and minimum values yield a range of 37 years. The standard deviation is 6.41. The value of skewness (1.52), Kurtosis (5.99) and Jarque Berra (102.25) indicates that the observations are not normally distributed (Verbeek 2008).
Scatter plots
A scatter diagram is a graph that plots two variables on a Cartesian plane. Scatter diagram tries to establish if there exists a linear relationship between the two variables plotted. This can be observed by looking at the trend of the scatter plots. The independent variable is plotted on the x – axis while the dependent variable is on the y – axis. In this case, salary will be plotted on the y – axis while the number of years will be plotted on the x – axis (Greene 2003). Different graphs will be plotted for each explanatory variable.
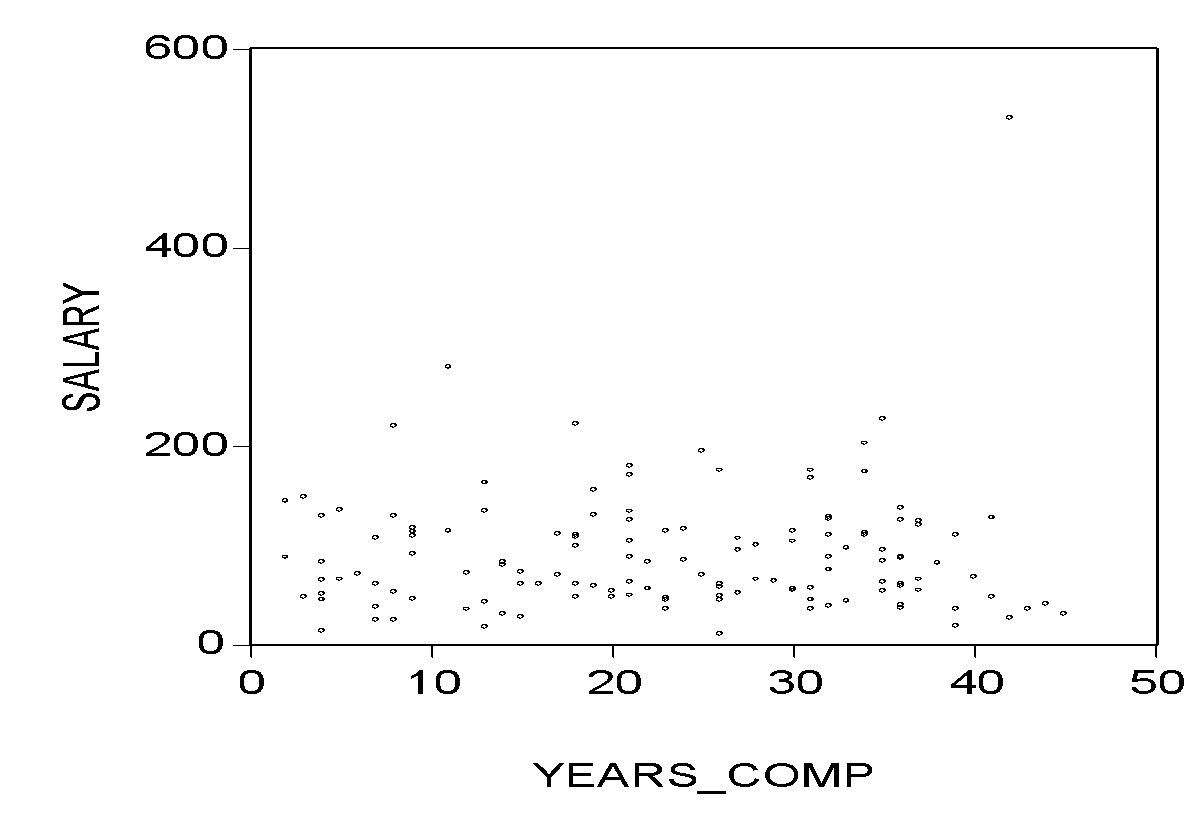
In the graph above, it can be noted that as the number of years the employees have worked in the company increases, there is no significant change in salary. This implies that there seem to be no sign of the relationship between salary and the number of years the employees have worked in the company.
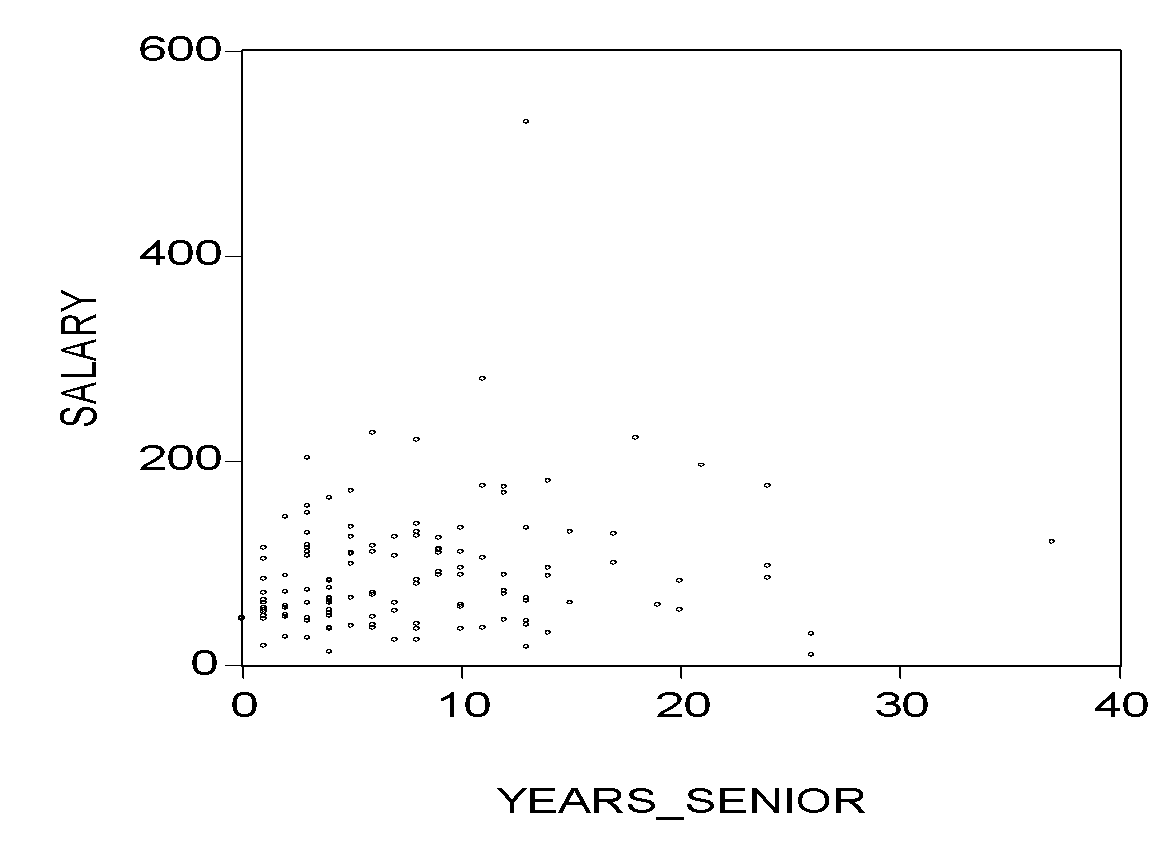
In the graph, it can be observed that the salary tends to increase as the number of years the employees have worked as seniors increases. The plots show an indication of a positive relationship between the two variables.
Simple regression
Simple regression develops a relationship between two variables. The dependent variable is salary while the independent variable is number of years. The regression line will take the form
when the ordinary least squares method is used (Asteriou & Hall 2011). The regression line can be simplified as shown below.
Simplified regression equation Y = b0 + b1X
Y = Salaries
X = the number of years they have worked for the company
The theoretical expectations are b0 can take any value and b1 > 0.
Regression results
Table 1.1 shows the regression results for salary level against the number of years they have worked for the company.
The regression equation can be written as Y = 84.79 + 0.25X. The value of R-squared is 0.0022 while t-statistics is 0.5461 (it is less than t-tabulated at 95% confidence interval – 1.932). The results do not show a strong regression line.
Table 1.2 shows the regression results for salary level against the number of years they have been senior officers.
The regression equation can be written as Y = 77.40 + 1.69X. The value of R-squared is 0.0301 while t-statistics is 2.0332 (it is greater than t-tabulated at 95% confidence interval – 1.932). The results show that the variable is a significant determinant of salary.
Discussion
The regression results for the relationship between salary and the number of years they have been senior officers is more robust than the relationship between salary and the number of years they have worked in the company because it has a higher value of R-value and years_senior is a significant explanatory variable.
Confidence intervals
The confidence interval is calculated based on the values of the sample collected from a given population. It gives the range within which the population parameter is expected to lie. Further, the population parameter is not known (Baltagi 2011). Therefore, the confidence interval does not give the exact value of the population parameter. The intervals will be calculated at 95% confidence level.
Table 1.3 shows the confidence interval for the number of years they have worked for the company.
The population parameter for years_senior will lie between 0.0461 and 3.3437.
Table 1.4 shows the confidence interval for the number of years they have been senior officers.
The population parameter for years_comp will lie between -0.6647 and 1.1718.
References
Arnold, R 2011, Economics, Cengage Learning, USA.
Asteriou, D & Hall, S 2011, Applied econometrics, Palgrave Macmillian, London.
Baltagi, G 2011, Econometrics, Springer, New York.
Greene, H 2003, Econometric analysis, Prentice–Hall, London.
Verbeek, M 2008, A guide to modern econometrics, John Wiley & Sons, England.