Introduction
The term ‘acoustic’ is synonymous with the study of sound waves and their effects. In a synopsis, this study basically centers on the consequences of wave motions across the three states of matter including solids, liquids and gasses. As such, the scope of acoustics cut across array of disciplines, and to this effect, the terms, for instance, psychoacoustics and bioacoustics are popular among acousticians. Moreover, acoustics find application in technical fields including noise control, transducer technology, design of theatre halls, and “sound recording and production” (Finn et al. 103). With regards to the scope of this paper, our main interest is centered on sound absorbers and how they are applied in room designs.
The reverberation time (T60 = 0.16V/A) as derived by Sabine is the most vital formula when it comes to room acoustics. As such, on predicting T60 of materials one is in a better position to determine the surface, acoustic characteristics of a room and hence; clad a room appropriately. Principally, in order for one to achieve an ideal room design meant for a specific application, an acoustician need to have knowledge on “absorption coefficient per octave band” (Finn et al. 103) of a diversity of materials. In a nutshell, in a room, materials including wooden doors and windows are known to absorbing sound of low frequency.
In the contrary, fabrics and clothes are known to absorbing middle and high frequency sound waves. Consequently, one can strike a balance between these materials so as to achieve appropriate T60 versus frequency combinations in a room. In a synopsis, the specific objective of this paper is to introduce and hence appreciate the physical mechanisms vital in sound absorption cum reverberation control. To this effect, the knowledge of sound absorption coefficient would come in handy when describing the properties of these materials. In some places, for example, in churches, there is a general demand for control of reverberations. As such, this paper will try to demonstrate how an effective room design dampens these effects.
The method used to determine sound absorption
Generally, the inner surfaces of a room receive sound from a wide diffuse field typified by the figure below:
Consequently, this chapter describes a relevant sound absorption method that would be used to determine the sound absorption coefficient emanating from the above incidence. This method is also reffered to as the reverbaration room method. Ideally, the experiment is performed in a “reverbaration room with highly irregular or non parallel surfaces and/or suspended, sound defusing elements” (Finn et al. 103). The assumption in this experiment is that the varied sound field would concur with the requirements stipulated in Subine’s reverberation formula. To derive Subines formula we assume that a vacant reverberation room has the following parameters; an absorption coefficient, αempty, inner surface area, S, and has a volume, V, then the below equation is derived:
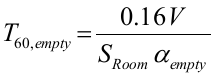
In this room an introduction of a foreign material, Ssample, changes the entire equation to:
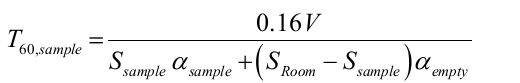
On combining the two equations and eliminating S yields the equation below:
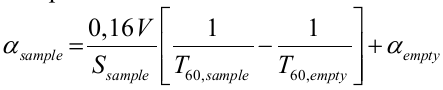
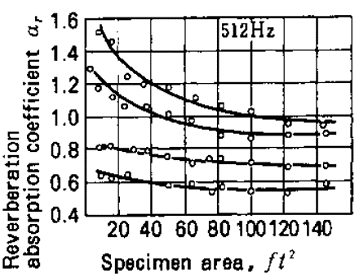
The above equation is fundamental in determining the coefficient, αsample, of a foreign material. Importantly, the measurement is “normally carried out in 1/1 or 1/3 octave bands from 100 to 5000 MHz” (Finn et al. 104). The results obtained in this method can only be credible if the size of the material sample relative to the area of the room is logical. Basically, if a very small material is introduced to an abnormally large room then the results obtained would be faulty (α>1) (see the graph below). This phenomenon is accounted for by the effects of diffraction of sound waves which dwarfs the absorption properties of the sample.
Type of sound absorbers
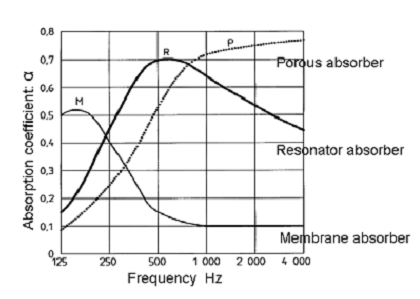
This chapter describes the most common types of materials used for sound absorption. These materials include the membrane, resonate and porous absorbers. This section tries to relate the absorption coefficient of these materials to the frequency of the same as typified by the graph below:
Porous Absorbers
Porous absorbers are common in our houses and they are presented in numerous forms including garments like curtains, furniture, carpets, and the ceiling material. Porous materials are basically characterized by the presence of air pockets which can be pressed more or less thanks to the resistivity of the material. Chiefly, the absorption property of a material is a function of the friction drag force present in air molecules under motion, and the nature of the material in contact with the air where heat transfer happens (from kinetic in sound to heat energy on the material).
Taking into account a scenario where a sound wave is incident but normally on a porous material mounted on a rigid surface, the trend exhibited by the graph below (left) of a standing wave together with its pressure amplitude on the left would result. The sound pressure coincides with the particle velocity.
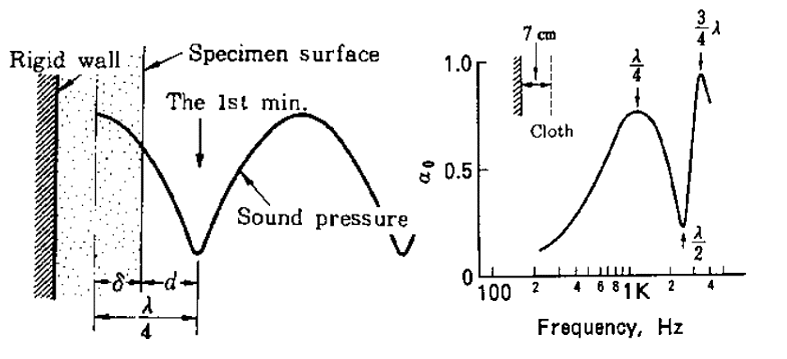
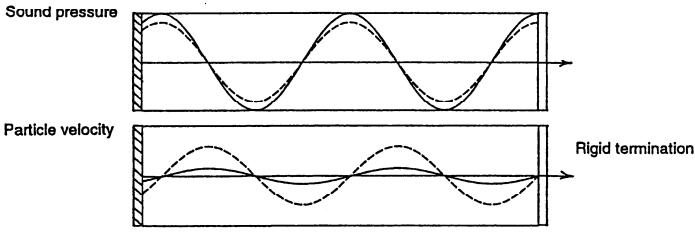
This is in contrast with when the same wave bombards a rigid termination (see figure below). Basically, the pressure and the particle velocity cancel out. The rational behind this analysis is that it aids in determining sound absorption efficacy of a material. Ideally, to achieve the best sound absorption efficacy then the thickness of a material should be at least greater than a quarter the wavelenght of the sound wave.
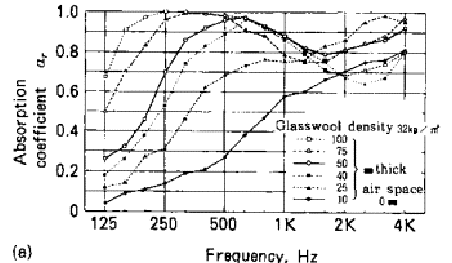
In a nutshell, sound absorbance efficacy of a given thickness of a material will be deemed to have failed if a certain threshold frequency of the sound wave fails to attain. The graph below portrays how absorption coefficient versus frequency differs with various thicknesses of a wool mat.
Membrane absorbers
A membrane absorber is a “kind of double walled sound absorber with an air-filled cavity sandwiched between the walls” (Finn et al. 106). The frequency of resonance (fo) of the entire setup is a function of the mass, m, of a unit area of a plate, and the spring ability of the enclosed air which depends on the deepness, L, of the enclosed air. This can be represented by the equation below:
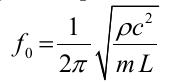
Nevertheless, this is limited to when the plate is absolutely limp. Other plate parameters e.g. stiffness as well as the mode of pulsation are vital in determining the resonance frequency. To this end, this value can be obtained using the expression below:
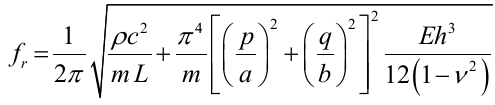
As such, the variables “a and b represent the dimensions of the material, h is the thickness while E and v are the Young’s Modulus and poisons ratio respectively” (Finn et al. 106).
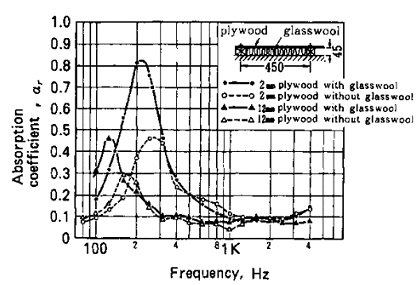
The graph below shows a plot of absorbance coefficient against sound frequency for two sample materials (plywood) having different thickness. Furthermore, one of the plates had been mounted with glass wool while the other one was without. The trends as attested by the graphs below confirm the above two equations. They reveal “that the thickness is inversely proportional to resonance frequency” (Finn et al. 106). Also, it has been established that the presence of a glass wool enhances the absorption efficacy. This also decimates the resonance frequency.
These absorbers are found in our houses typically as wooden floor surfaces, and they result in a controlled low, resonance frequency value contrary to concrete built rooms. The later, is synonymous with blurred sounds at low frequencies.
Resonator absorber
A more advanced system of a membrane absorber is a resonator which utilizes an oscillating air sandwiched in a double walled cavity. This has an opening on the surface to the outer atmosphere. To this effect the enclosed air act as a spring function (see the figure below).
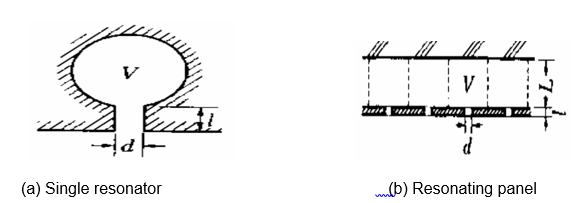
For type (a) the resonance frequency is obtained through the expression below:
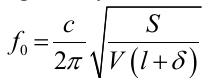
The variables S, V, l and δ represent the crossection area of the openning, volume of enclosed air, neck length and a correction factor respectively. However, this type of absober is not common since it has a very short frequency range. As such, a resonating panel overcomes the shortcomings of the former model by providing for a relatively wider frequency range. Thus, its resonance frequency is given by:
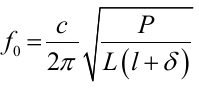
The variables P and L represent the extent of perforation and depth of the air pockets respectively.
As compared to a membrane absorber, a resonator is an efficient sound absorber. The damping efficacy and hence the sound absorbance can be optimized by mounting a monolayer of mineral wool in the perforations. Also, this can significantly be enhanced by the reduction of the pore diameters. Most common form of this type of an absorber is a perforated gypsum board.
Practical use of sound absorbers in room acoustics
The essence of understanding the physics behind sound absorbers is to equip oneself with the knowledge of how reverberation can be contained in room designs. This will in turn reduce noise and enhance intelligibility. Some states’ building laws, for example Denmark Building Law, clearly stipulates for an optimum T60 value for diverse working environs including schools and day-care institutions among others. Furthermore, this law recommends for specific designs for buildings including theatre and concert halls among others.
Room acoustic designers usually target the ceiling because it provides for manipulation since most of its surface is always unoccupied. Consequently, acousticians have come up with designs including suspended ceilings and mineral wool baffles that aid in damping reverberations. These designs are portrayed by the pictures below:

Principally, in room acoustics where a majority of sound absorbers are biased towards the ceiling, the T60 becomes a function of the room height. Therefore;
T60 =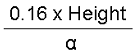
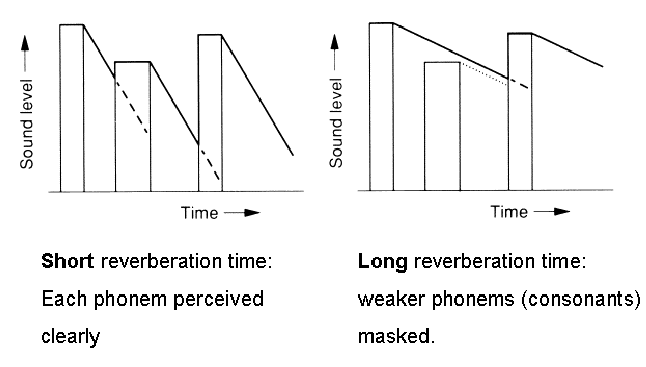
Many a public places demand for a noise free environ thanks to acousticians’ efforts in trying to dampen reverberation. However, an ideal situation requires for an intelligible speech too. To this effect, the figures below show how a delayed sound decay in a room can facade weak phonemes typified schematically as perpendicular bars. Basically, in speeches, a consonant element that is usually overlooked as a weaker sound can serve to jeopardize the intelligibility of a speech if the decay time is not checked. As illustrated by the schematic diagrams below, a long reverberation has a potential to extremely deteriorate the entire speech.
Works Cited
Finn, Jacobsen, Torben Poulsen, Jens Rindel, Anders Gade and Mogens Ohlrich. FUNDERMENTALS OF ACOUSTICS AND NOISE CONTROL. Odense: Department of Electric Enginearing, 2011. Print.