Introduction
Equation extraction from governing data can be difficult among scientists and engineers. Overfitting is avoided by balancing the models’ complexity with a descriptive ability. The study by Steven Brunton and others at the University of Washington demonstrates the use of Sparse Identification of Nonlinear Dynamics (SINDy). The algorithm can be used in several problems, from simple canonical systems to fluid vortex shedding.
Problem Description
With recent technological advancement data analysis software and programs have been developed, data distillation has remained slow (Brunton et al., 2016). Consequently, data extrapolation has been limited to attractor’s sampling and construction. For instance, the discovery of Kepler, although equipped with extensive and most accurate planetary data, lacked fundamental dynamic relationship description of planetary orbits (Brunton et al., 2016). Conversely, Newton’s discovery of the relationship between momentum and energy presented a dynamic model that can predict behaviors where data is unavailable.
Methods Used
Linear and nonlinear oscillators were used to demonstrate difficulties in simple canonical systems. Also, the study applied chaotic Lorenz system to demonstrate the challenges in simple canonical systems (Brunton et al., 2016). Most physical systems have limited number of relevant dynamic definition terms, limiting number of leading equations in high-dimensional nonlinear function space (Brunton, 2016). Algorithms in the unsteady fluid wake and nonlinear PDEs were also demonstrated by the study method (Brunton, 2021). After that, the dynamics were subjected to generalization to include parameters, time, and forcing.
System Discovery and Formula Used
The study reenvisioned a dynamical system discovery problem from sparse regression perspective and compressed sensing. The dynamical system considered was of the form:
, x(t) is the system’s state at duration t and f(x(t)) is the dynamic constraint (Brunton et al.,2016). Do determine f the collected data was sampled using the matrix: 
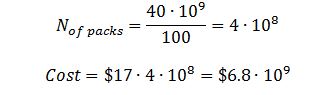
Next, a library of Θ(X) was constructed each consisting of non-linear functions of X’s column. Θ(X) consist of constants, trigonometric terms or polynomials. To determine active non-linear using the formula:
, each column of 
is a sparse vector that determines active terms. A model governing each equation was determined:
. Since 
is a symbolic functions’ vector of element x. Therefore, x=f(x)=ΞT (Θ(XT)) T
New Results and Possible Extensions
The work shows that generalizing the SINDy algorithm allows analysis of externally forced and controlled systems. Fields such as neuroscience, with big data without governing equations can apply the new results from the study. The works present the discovery of standard forms by including optimization parameters, thus making a significant step towards unassisted dynamical systems’ identification.
Chaotic Lorenz system formula: x=σ (y− x), [7a]
y= x (ρ− z) −y, [7b]
z=xy −βz, [7c]
The data collected was stored matrices X and 
. For the PDE coordinate system, the mean-field model for the cylinder was:
x= μx −ωy+Axz, [8a]
y= ωx+ μy+Ayz, [8b]
z= λ (z− x2 − y2) [8c]
When λ is large the z dynamics are fast and the slowing manifold z= (x2+ y2). The vortexes should be shedding.
For bifurcations and parameterization, the SINDy algorithm was encompassed to allow discovery of normal forms (31, 50). Parameter μ was appended into the dynamics:
x=f (x; μ) [9a]
μ= 0. [9b]
Identifying f (x; μ), a sparse combination of x and μ was easy. 1D logistic xk+1 =μxk (1−Xk) +ηk.
2D Hopf normal form (51)
x=μx+ ωy−Ax (x 2 +y 2)
y= – ωx +μy−Ay (x 2 +y 2)
Time dependence and external forcing μ are added to the vector field: x= f(x, u(t), t), and t= 1.
Conclusion
While data science seems a panacea for scientific and engineering problems, it only provides a principled approach to leveraging data. Traditional systems to dynamic and big data available are prone to overfitting: statistical data models fit precisely against their training data. Therefore, algorithms producing parsimonious models are desirable. The work applied sparse regression in determining dynamic equations that accurately represent data. Generalizing the SINDy algorithm used in the piece makes it possible to analyze forced and externally controlled systems. Therefore, the new results are beneficial to climate science, epidemiology, financial markets, and other scientific and engineering fields with big data.
References
Brunton, S. L., Proctor, J. L., & Kutz, J. N. (2016). Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proceedings of the National Academy of Sciences 113(15), 3932-3937. Web.
Brunton, S. (2016). Sparse identification of nonlinear dynamics (SINDy). YouTube. Web.
Brunton, S. (2021). Sparse identification of nonlinear dynamics (SINDy): Sparse machine learning models 5 years later! YouTube. Web.