This lab work examines the use of the vector addition rule to determine the resultant force on a force table. Three tests are performed in which several pulleys are fixed, and others are connected to a force sensor. The equilibrium between the pulleys is achieved by manipulating the free pulley. As a result of the experiments, all data were recorded. Thus, the table below shows the results for each of the three runs, with the last round using four pulleys instead of three. In addition, the table shows the uncertainty values calculated as half the minimum measurement on the device, be it a scale or a degree ruler.
In the coordinate plane (mass, degrees), three vector sums were plotted, and free-body diagrams were shown. The corresponding diagrams are shown in the figure below. To construct the vector diagrams, each vector was initially plotted from the zero point according to the given characteristics and then was moved by parallel transfer to the end of the previous vector. Thus, only two of the three diagrams were closed, as shown in the figure below.
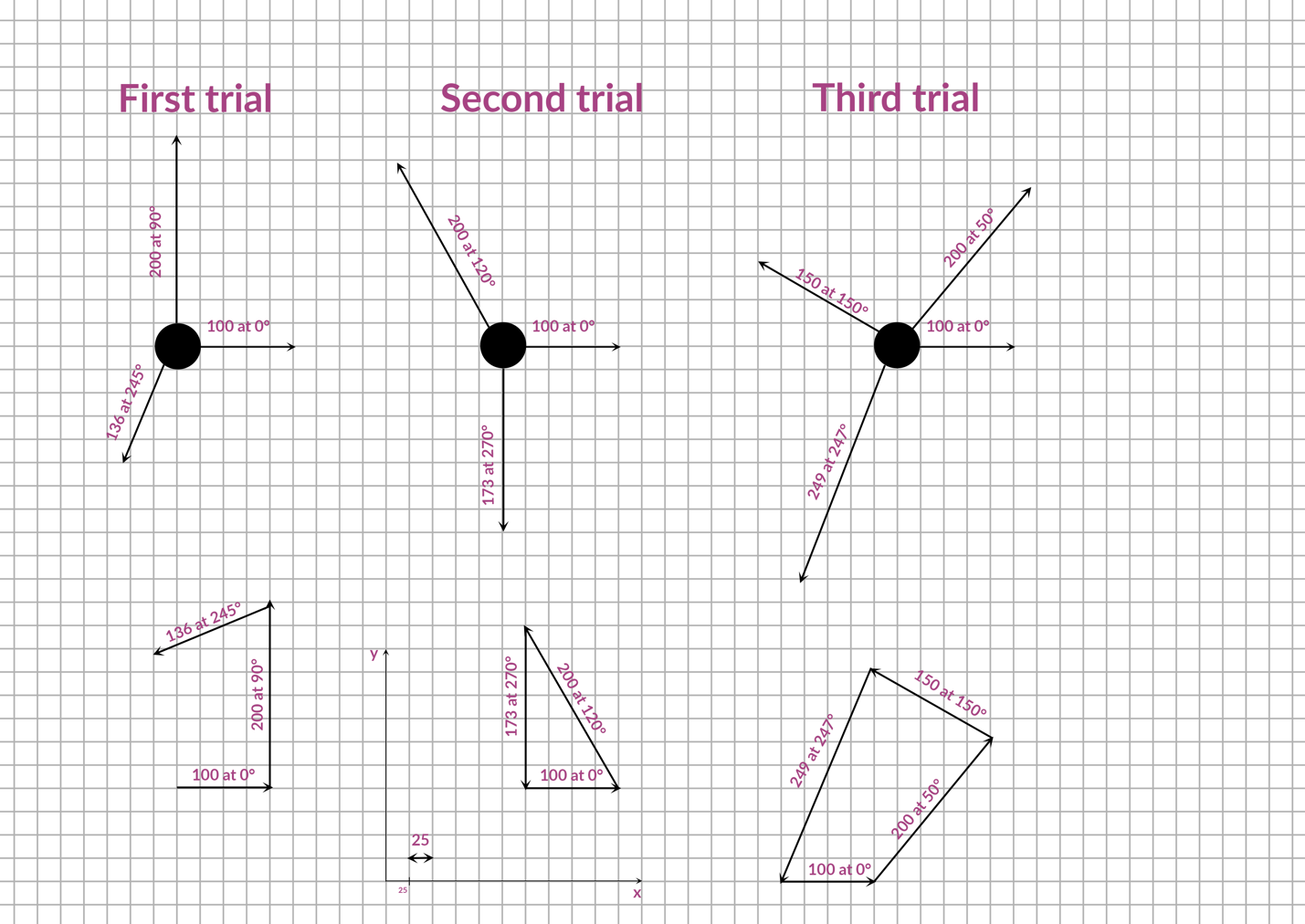
For each of the ten vectors, it is possible to write coordinate pairs based on projecting the vector onto perpendicular axes. For more precise calculations, the projections were obtained by multiplying the vector length (mass) by the cosine or sine of the corresponding angle according to the Pythagoras rule (Zeeshan, 2021). Thus, all vectors will have the form as shown in the table below.
The vector sum was calculated by adding the x- and y-coordinates for each run in pairs. It can be seen that the only system in which equilibrium was reached is the second trial. The equilibrium is determined by the final sum: if it is equal to zero, then the equilibrium has been reached. We can say that equilibrium has been proved for the third system as well, since the final force has coordinates extremely close to (0, 0), and a slight deviation can be due to errors, uncertainties, or rounding. In contrast, no equilibrium has been reached for system number 1, as the sum follows. The values are too far from the zero coordinates, so no equilibrium force existed in this system. It is also worth noting the role of uncertainty in the calculations: it is uncertainty, that is, known measurement errors, which can lead to the situation that occurred in the third run, when the equilibrium force was slightly different from (0, 0). Thus, uncertainties should always be taken into account in calculations. Thus, the laboratory work has shown that the rule of addition of vectors can indeed be used to study the equilibrium force on the force table. In the case where the coordinate pairs of the resulting force were not equal to zero, there was no true equilibrium in the system.
Reference
Zeeshan. (2021). Cathetus on a right triangle?DGT.