Introduction
With the emergence of globalization, the world stock markets have become interdependent thereby if there is a change in one stock; the ripple effect is felt in other stocks in terms of volatility and returns. In this review we examine how the volatility of Irish stocks has evolved since 2000 to 2009 and the factors that have influenced them.
In focus are the main factors that influence the volatilities and how correlated the volatilities are in the different industries. In this review, we shall look at the influence of the U.S policies on the American stock market and in return the effect on the Irish stock market (Bredin et al, 2004).
There several ways through which the information about expected changes in financial policies are conveyed to the investors. From past studies it has been shown that investors invest in stocks prior to release of policy news which they hope will serve to their advantage. Therefore after the policy information has been past, the investors react accordingly, and this phenomenon is referred to as “the calm before a storm effect”.
Bredin et al. (2005) found evidence of a calm before the storm effect and of an asymmetric response to unexpected US policy changes, in that a higher than expected policy rate rise increases ISEQ volatility by significantly more than a lower than expected rise. Kearney (1998) stated that the Irish stock market is “highly integrated with the important international stock market in London”.
He finds that a predominant cause of volatility in the ISEQ is volatility in the FTSE. He also states that “Ireland’s membership in the European Community and the European Monetary System ensures that its financial and real business sectors are also closely linked to international developments”. Finally he finds that interest rate volatility is a less significant determinant of volatility in the index than exchange rate volatility.
Due to the membership of Ireland to the European Union, the volatility of ISEQ has significantly reduced and also the effect has been the same in other member states.
Also, during the survey of the ISEQ 20 index a number of methods were applied for example the CAPM theory that holds, the higher the security returns are equally proportional and that stock investors have equal price expectations, hence the investors who have diversified their stock portfolio have a less unsystematic risk.
Nevertheless it is normally occurs the returns in securities and different markets are not directly proportional. Kearney (1998) shall analyzes how the policies are made and by whom and the variables that they seek to change in the financial markets.
Rationale For The Study
Stock and financial researches conducted recently have shown a tremendous change in the way investors, both foreign and domestic, have changed their pattern of investing in the stocks. Since the global economic down turn, the volatility of the Irish stocks has increased drastically. This has been influenced by the number of economic and non economic variables.
Due to increased awareness of the volatility of the stock market by investors, a number of them diversified their stocks options to avoid unsystematic risks that would normally occur in the stock markets. The graph below shows the performance for the past decade: (Davis, The World’s Worst-Performing Stock Market).
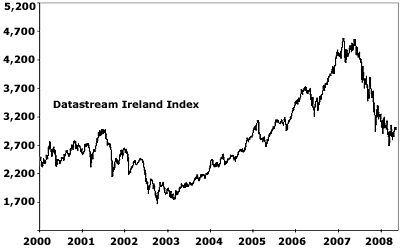
There many theories used in the explanation of volatility of the Irish stocks. Bomfim (132) advocates for the Capital Asset Pricing Method (CAPM). This theory gives the assumption that asset returns are random variables that are distributed normally hence investors have diversified portfolios that assist them in eliminating risks.
Due to the fact that equity returns in the market are not distributed normally, there s usually a standard mean deviation of 3-6 which occurs often. In addition, there are other external factors that influenced the volatility of the Irish stocks, for example the influence of the international policies that had a direct impact in the value and trading of the stocks. The simplified market model is shown as follows , = b +e = +h (1)
Here, i t r , is the excess return on asset i at time t, m t r , is the excess return on the market portfolio, i b is the asset’s beta coefficient, i,t e is the usual CAPM idiosyncratic residual, and i,t h is the market-adjusted excess return on asset i computed according to the simplified market model.
Letting i t w , denote the weight of asset i in the market portfolio, we can compute the weighted average of the variance of returns on the n stocks in the market portfolio. t i t w Var r Var r w Var w Cov r , 1( ) ( ) (h ) 2 ( ,h ) (2)
By substituting for i,t h from (1), noting that m t r , and i,t e are orthogonal, and recalling that the weighted average of the i b coefficients is equal to 1, the last term on the right collapses to zero, and we are left with the Carrol (2007) variance decomposition. This decomposes the average excess return variance across all assets in the market portfolio (VARt) into two components; the variance of the excess return on the market portfolio (MKTt) and the average firm-level variance (FIRMt).
It provides a CAPM-equivalent decomposition of average total risk into market risk and average idiosyncratic risk, with the considerable advantage that it by passes the need to estimate betas for each firm.
Carrol (2007) note that rising average idiosyncratic risk, together with unchanged market risk, implies a decrease in the average correlation amongst the portfolio’s assets, but they do not provide a theoretical specification of this relationship.
Although it is intuitive that average correlation must decline if the average idiosyncratic risk rises with a constant level of market risk, it is not trivial to predict what patterns in average correlation might emerge when, for example, average firm-level risk and market risk vary in the same direction but at different rates of change. To see the full set of possible configurations of market and idiosyncratic risk, we rewrite the MKT term by converting it to matrix notation.
The equation tells us that, at least for an equally weighted market portfolio, we can interpret average correlation as the parameter that, for any given level of average total risk, divides the latter into market risk and idiosyncratic risk. By differentiating rt in respect to the ratio of average idiosyncratic variance to average total variance, we obtain dr d( FIRM / VAR ) t = -1
Equations show that the variation in average correlation is inversely proportional to the variation in the ratio of average firm-level variance to market variance. The larger the number of stocks included in a portfolio, the more it resembles an equally-weighted portfolio and the better is the approximation provided by the equation.
Average correlation is strongly influenced by the extent to which firms diversify internally. The more the average firm diversifies (the more it resembles the market portfolio), the higher will be the average correlation for each given level of covariance risk in the economy (MKTt). The opposite is true for average firm-level variance.
Stock values are usually determined by use of their net present values therefore should a change in policy affect the expected net present value; the effect will be reflected in the value of stock returns in several ways. Through the use of arbitrage, new policy changes will change the market rates of stocks hence affecting the opportunity cost for an investor in continuing to hold such stocks.
Therefore it will affect inversely the NPV of future cash flows from the stocks against the discounting factor. In addition change in international policy will affect the productivity of the stock in the short to medium term.
The U.S monetary policy changes have also contributed to the volatility of the Irish stock through policies that impact the supply of money, non- borrowed money in reserves, the discounting rate and the targeted rate set by the federal reserve.
Monetary policies are usually undertaken by the central bank over a given period in time which they find suitable. The policies made usually take into account the time or period of interest and the variable that the central bank wishes to control. Early studies estimated the following model:
_Pt = a + b(_Mat − _Met ) + _t (1)
Where: _Pt is the percentage change in the stock price;
_Mat is the announced change in the money stock;
_Met is the expected change in the money stock obtained from survey data; and
_t is the error term.
With the change in monetary policy regimes towards targeting short term interest rates, more recent studies examine the impact of changes in the policy rate target on asset prices. It still begs the question of how to decompose policy rate changes into (un)anticipated changes.
With the advent of federal funds future contracts in the late 1980s researchers have focused on the information contained in the federal funds futures rate to identify expectations of changes in future policy.
Changes in monetary policy decision have been including in the mean equation whereby the main focus is restricted to the days when the monetary policy decision was made. This is usually done in order to control other variable that might have occurred during those days. In addition it is also done in order to control other variables that influence the rate of returns of the assets.
Real variable that have been included in the equation include the GDP and the unemployment figures in the region while nominal variable have included the rate of inflation, money supply and the interest rate decisions. Any policy announcements are usually made in two ways; there are policy changes that are usually fixed to be announced at a particular time thus one knows when the change takes effect on the calendar
Campbell et al (2001), notices that the conditional volatility of the Irish stocks is greatly influenced by the integration of the international stock markets. Particularly, the London and the EC stock markets play a major role in the volatility of the Irish stocks hence whatever influence they face; its effect will be seen on the Irish stocks.
In addition, the European stock market ensures that the financial and business policies in the region are implemented by all the members and ISEQ complied with the policies thus is subjected to the same forces as other stock markets in the region. However, there has been a controversy between the influences of the GARCH model on whether it affects the volatility of the ISEQ or not.
The GARCH volatility model is used in getting the returns of equity since it is modeled in the belief that returns and volatility are interdependent. The return in equity is given by the following formulae:
Rt = ln (St )/St−1
Where; St = closing level security of the day our proxy for the unanticipated change in the German policy rate between 1989 and 1998 is the first day change in the 3-month Euromark futures rate.
With the introduction of the euro in January 1999, we proxy surprise changes in the ECB policy rate by the one day change in the 3-month Euribor futures rate.9 For the UK, our proxy for the unexpected change in the policy rate is the one day change in the 3-month sterling futures contract. Finally, we also analyse the impact of Irish interest rate changes on the ISEQ.
Given our methodology, an obvious problem is the lack of a futures market for Ireland stock market. We attempt to circumvent this problem by defining the unexpected change in monetary policy as the one day change in the 1-month Dublin interbank offer rate (DIBOR).11 The DIBOR was closely related to the Short-term Lending Facility (STF), the rate at which the Central bank uses. Early studies estimated the following model:
_Pt = a + b(_Mat − _Met ) + _t (1)
Where _Pt is the percentage change in the stock price;
_Mat is the announced change in the money stock;
_Met is the expected change in the money stock obtained from survey data; and
_t is the error term.
With the change in monetary policy regimes towards targeting short term interest rates, more recent studies examine the impact of changes in the policy rate target on asset prices. It still begs the question of how to decompose policy rate changes into (un)anticipated changes. With the advent of federal funds future contracts in the late 1980s researchers have focused on the information contained in the federal funds futures rate to identify expectations of changes in future policy.
When determining the volatility persistence of the Irish stocks, one looks at three key issues, mean reversion, volatility clustering and persistence, and the volatility half life. These three factors determine how long the volatility effect on a stock will last.
There are numerous external factors that are considered in determining the volatility of Irish stocks. For the Irish stock market in the last decade, the stability of inflation and output has been greatly influenced by the significance of the monetary policy.
The monetary policy affects the stock prices in various ways. First, alterations in the monetary policy significantly influence the output in the short and medium-term, and also the changes affect future cash flows by the alterations in markets. Secondly, through arbitrage, the change in the monetary policy rate also affects other market returns, thus determining the opportunity cost of investing in such stocks.
Bredin et al (2004) studied the effect of changes in monetary policy on treasury stocks and discovered that policy rate changes increase the treasury rates especially in the short term. Bredin et al (2004) says the introduction of a common European currency and the recent tendency of stock prices has shown the correlation between the monetary policy and security prices.
The decomposition of the Irish policy rate changes into (un) anticipated parts also significantly affects the volatility of the market. However, with the emerging relevance of interest rates in future markets, investors can derive market expectations of policy variables. Also, the markets are driven by the expectations theory of the term structure of interest rates.
Coval (2001) observes that changes in United States policy rate negatively influenced the volatility of the Irish stock market in the past decade. For the US, unexpected alterations in the federal funds target rate had an adverse effect on the ISEQ returns.
Domestically controlled interest rates also have an influence on the Irish stock market. Kearney (1998) studies conditional volatility of shares and concludes that the asymmetric component there is a significant correlation between conditional volatilities and correlation estimates, and the dynamics of firm-level correlations.
Relationship to previous studies
A great deal of current literature regarding individual stock volatilities has been based on the findings of the 2001 paper by Xu, Malkiel, Campbell and Lettau. It had been previously assumed that unsystematic risk accounted for little in explaining the volatility of stock returnsMany studies done on the Irish stock market have been based on the findings conducted in 2008 by Carrol & Collins.
It had been assumed that unsystematic risk had no or less influence in the volatility of stocks but that investors had portfolios that were fully diversified and thus less prone to risks. In order to explain this issue, Campbell suggested that on industry level, volatility of the stocks was of interest to the investors since they had large stock holdings which may not have been diversified as suggested by other financial theories.
Studies by Campbell have put forth a number of ideas to explain the various causes of volatilities for example, leverage, financial innovation and changes in executive compensation. He also concluded that the U.S stocks were not as volatile as believed.
Kearney et al (1998) studied the volatility of stocks found in the European market. They suggested that the European stocks trend moved in the same direction as the U.S stocks in such a way that majority of the stocks were diversified thus a positive idiosyncratic volatility.
Bredin et al. (2004) studies showed a “calm before a storm” effect which he suggested that it resulted from unexpected US monetary and financial policy. Therefore if a higher rate policy is expected, the ISEQ volatility increases by a significant ratio.
Source of data
The data collected for this review was from the ISEQ 20. The data was analyzed from 2000- 2009 which gives a ten year period to effectively determine the factors influencing the volatility and correlation of the Irish stocks.
The information gathered also looked into the international factors influencing the volatility of the stocks.
Proposed methods
For the purpose of this study, I looked into the return on equity methods as put forth by Flannery & Protopapakis (2002) where he divided his study into three issues, market level and idiosyncratic firm level. Campbell approach the matter by showing that returns will be decomposed without requiring the estimation of covariance’s or betas for industries or business.
Campbell et al (279) defines this as follows:
Rjit = excess returns of jth stock, in ith industry, at time t;
Rit = ∑jei wjit Rjit = excess returns of ith industry at time t;
Rmt= ∑iwit Rit = market excess returns at the time t.
To measure the industries volatility, one can use CAPM which is defined as: Rit =βim Rmt + eit.
However in this case the variable, (eit ) that is estimated using the first equation, requires that one has the knowledge of βim taking into assumption that the CAPM theory is the equilibrium model. Alternatively, one can use; Rit = Rmt + eit.
However, Rmt and eit are not orthologonal, hence we shall use, Var(Rit = Var(Rmt ) + Var (eit ) +2Cov (Rmt, eit)
Since the equation above contains the industries beta, the Var(Rit) will contain the covariance between the Rmt and eit. However it does not require for one to be aware of the covariance between Rmt and eit to estimate the weighted average industry risk.
Secondly, Carrol & Collins (325) looked into the different volatility models applicable to the ISEQ. Thus I plan to use econometrics tests in the application of data before making a final decision on the specific model and procedure to choose.
Kuttners (2001) approached the issue with the following regression analysis of the ISEQ; _ISEQt = _0 + _1_FFet + _2_FFut + _t
Where:
_ISEQt = is the percentage change in the ISEQ index between t and t+1;
_FFut is the first change in the federal funds futures rate on day t of a change in
the federal funds target rate;
_FFet is the expected change in the federal funds target at date t.
Thus the expected rate in change in the federal funds will be calculated as the difference between the federal fund rate target and the rate of change in the expected in the future.
In addition, we shall look into the (un)expected changes occurring in the European stock markets. Since there are no financial instruments that keep check on the trends of the policies rates, we can use interest rates future contracts since they are influenced by the current market expectations. In addition the impact of the Irish domestic interest rates plays a great influence in the changes in the ISEQ.
Due to lack of future markets in Ireland, we shall use the Dublin interbank offer rate which is used by the central bank in lending to banks and in turn the rate is reflected in the Dublin wholesale market (Gurkaynak & Sack, 2002).
Conclusion
Coval (2001) studies put +forth have shown that the ISEQ, volatility has declined over the time. In particular there was a decline in volatility before announcements in change financial markets.
Hence the Irish stocks appear to be dependent on the monetary policies made by the U.S. Bredin et al. (2005) shows that there is a direct influence of international and domestic interest rates whish directly influence the volatility of the Irish stocks Our purpose in this paper has been to examine the trends in market and firm level volatility in European equity markets.
Using over 2,300 daily observations from 2000 to 2008 on 6 European market indices and 42 stocks from the Eurostoxx50 index, we analysed the time series behaviour of market risk, idiosyncratic risk, and aggregate correlations between the indices and between the individual stocks.
In addition to extending the Davis (2008) methodology to provide a full description of the relation between changes in market risk, aggregate idiosyncratic risk and return correlations, we also applied the asymmetric version of the DCC-MVGARCH model of Bredin (2004) and Kearney (1998) to capture the time series behaviour of the conditional correlations between the market indexes and between the individual stocks in the Eurostoxx50 index.
In addition to the market risk in the U.S. and in Europe, we find that both market risk and aggregate idiosyncratic risk appreciate in our sample, and that the deterministic time drift at work in the latter is stronger than in the former. The rise in idiosyncratic risk implies that it takes more stocks to achieve a given level of diversification, and is consistent with the results reported by Davis (2008) for United States markets.
We also find that aggregate firm-level return correlations are trended weakly downwards in the euro-zone. Part of this finding might be explained by the fact that our sample includes large stocks that have a significant degree of diversification built into the cash flows associated with their businesses.
In contrast to this, however, the average correlation amongst the 5 euro-zone stock market indices and the Eurostoxx50 index has risen significantly over our sample period. This, we argue, is not surprising in view of the ongoing process of economic and financial integration in the euro-zone area.
In applying the DCC-MVGARCH model to further examine the behaviour of euro-zone correlations, we find that, consistent with Davis (2008) and Bom (2003), all our conditional correlation time series estimates display significant degrees of persistence.
At the market index level, we can reject the restriction that the parameters of the correlation process sum to unity, but there is strong evidence of a structural break in the mean shortly before the introduction of the Euro. This explains both the strong persistence of the correlation time series and its significant rise over the sample period.
We also find that the conditional correlation process is strongly asymmetrical with a negative but very small deterministic time trend. The asymmetry of the stock returns correlation process also explains why the shiftiness of market index returns, as reported in Table 2, is always negative whereas stock returns have either negative or positive shift.
Our finding that correlations amongst euro zone stock returns display a much weaker tendency to decrease than reported by Davis (2008) suggests the existence of different correlation dynamics in the euro-zone area and in the United States, at least over the portion of our sample period that overlaps (from 2000 to 2009). A number of explanations of this disparity can be tentatively advanced.
Commensurate with a corporate culture in Europe that emphasis external capital markets somewhat less than in the United States, companies in Europe have probably pursued less diversification strategies than in the United States. Another possible explanation is that the tendency for companies to access the equity market at earlier stages in their life cycle is less pronounced in Europe than in the United States.
Moreover, the level of average correlation in our sample, especially in the case of the DCC-MVGARCH estimates, is generally higher than in the Davis (2008).
A higher ratio of market to total variance and a lower ratio of firm-level to total variance, this suggests that the portion of total risk represented by idiosyncratic risk in euro-zone equity markets might be smaller than in the United States, implying a lower benefit to diversification in the European markets.
In other words, the opportunity-cost of not diversifying is relatively lower. Part of this difference might be explained by the fact that our sample comprises large stocks that have a significant degree of built-in diversification.
Nevertheless, our results suggest that fund managers should think through the full ramifications of seeking more cost-effective diversification by adopting the passive strategy of investing in market indexes rather than a selection of stocks from each country.
Reference List
Bom, M.,(2003). Preannouncements news and volatility. Journal of banking and finance, Vol 27, 133-151.
Bomfim, A.(2001). Making News: Financial Markets Effects of Federal Reserve Disclosure Practices, Manuscript. Federal Reserve Board, Vol 21. 121-132.
Bredin, D. Caroline G.,& Gerard, O. (2004). The influence of domestic and international interest rates on the ISEQ. The Economic and Social Review, Vol. 34, 249–265.
Bredin, D., Caroline G., & Gerard, O. (2005). US monetary policy announcements and Irish stock market volatility. Applied Financial Economics, Vol. 15, 1243–1250.
Campbell, J. (2001). Have Individual Stocks Become More Volatile? An Empirical Exploration of Idiosyncratic Risk. Journal of Finance Vol 56, 1-43.
Carrol, T., & Collins, J. (2007). Volatility models and the ISEQ index. Journal of financial report, Vol 23, 12-24.
Coval,M. (2001).The Geography of Investment: Informed Trading and Asset Prices. Journal of Political Economy,Vol 109, 811-841.
Davis, I. (2008). The World’s Worst-Performing Stock Market. The Growth Stock Wire, 8. Web.
Flannery, M., & Protopapakis, A. (2002). Macroeconomic Factors do Influence Aggregate Stock Returns. Review of Financial Studies, Vol 15, 751-782.
Gurkaynak, R., & Sack B.(2002). Market based measures of monetary policy expectations. Finance and economics Discussion series working paper, Vol 40, 658-721.
Kearney, C. (1998). The causes of volatility in a small, internationally integrated stock market: Ireland, July 1975 – June 1994. The Journal of Financial Research, Vol. XXI, 85-104.