How CAPM can be used to estimate the cost of capital for real investment decisions
Real investment decisions are very different from financial investment decisions. Financial investment decisions are concerned with financial instruments, which are usually traded on stock exchanges. This makes it easy to estimate the expected returns on such investments. In contrast, real investment decisions involve real assets such as land, technology, people, and other and other tangible assets. These assets pose difficulty in estimating the required returns.
The Capital Asset Pricing Model (CAPM) provides a solution to this problem. It states that investors require to be compensated both for taking a risk and for holding their money for a given period. The CAPM formula is:
Expected Return = Risk-Free Rate + ß(Expected market return-Risk Free rate)
In this case, ß represents the Asset Beta. This figure shows how easily the asset returns respond to changes in the market returns. Large ß shows that the asset’s returns are highly dependent on market returns, while small ß indicates that the asset’s returns are independent of the market returns. In the case of Ameritrade, the estimated Asset Beta is 2.06. This figure is very high. It reflects the fact that the returns on the proposed investment are highly dependent on the market returns. This is very risky. The result is that investors will require to be compensated highly for taking this risk. This is reflected in the resultant high cost of capital (22%).
The Cost of Capital can be estimated using CAPM provided the Asset Beta, expected Market Return, and Risk-Free Rate is known. In the case of Ameritrade, the asset beta has to be estimated from comparable firms. The risk-free rate is taken as the return on government securities of the same length as the intended investment period.
Risk-Free Rate and Risk Premium estimates for Ameritrade
My estimate for the Risk-Free Rate is 6.61%. This is the Annualized Yield to Maturity on 30Year government bonds. The reason I chose 30-year bonds as opposed to other short-term bonds is that this is a long-term investment decision. The company is planning to spend a lot of money on this project while expecting returns for an equally long period. Thus, this is the best proxy for the Risk-Free rate.
My estimate for the Market Risk premium is 7.2%. I obtained it by computing the difference between the Average Annual Returns of Long term bonds and Large Company stock between 1929 and 1996. I chose 1929-1996 from 1950-1996 because the latter period is shorter than the former. Therefore, the 1926-1996 period is likely to give more accurate results than 1950-1996.
Computation
Large Company Stocks- Long Term Bonds
= 12.7% – 5.5%
=7.2%
Steps for computing the asset beta for purposes of calculating the cost of capital
The first step in the process is to compute the monthly returns of each firm or asset. The data in Exhibit 5 about stock prices is relevant for this purpose. The monthly returns depend on the price of the stock, the time differences, and dividend issued. The formula for computing returns on a normal month with no stock split is as follows:
Return = (Pt+1 – Pt + Divt+1)/Pt
However, in case the company has a stock split, the formula changes slightly to accommodate this. It therefore becomes:
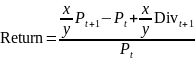
The VW NYSE or EW NYSE can now be used to compute the equity beta. I chose to use the VW NYSE. In this method, the regression analysis of both the monthly returns( x) and the VW NYSE (y) is used to estimate the beta. I used the Excel inbuilt function of SLOPE to carry out this analysis. I focused on the most recent 5 years of returns. The result obtained was the Equity beta of each of the comparable firms.
To obtain the Asset Beta for each of the firms, proceed to un-gear the Equity Betas. This is done using the Debt-Value ratios. In this case, they were provided in Exhibit 4. After un-gearing all the Equity Betas, estimate the Asset beta for the firm in question (Ameritrade) by getting the average of all the comparable Asset Betas. i.e
Computation
Charles Schwab-2.116
Quick & Reily-1.7879
Waterhouse Investor Services-2.3038
Average= (2.116+1.7879+2.3038)/3 =2.06931
Firms recommended as benchmarks in estimating the cost of capital
There are three different types of firms in Exhibit 4. The first set is the Discount Brokerage firms Quick & Reilly Group, Charles Schwab, Waterhouse Investor Services, and E*Trade. The second set is the internet companies Mecklermedia, Netscape, and Yahoo. The final set is the Investment service companies A G Edwards, Bear Stearns, Lehman Brothers, Merrill Lynch & Co, Morgan Stanley Dean Witter, Raymond James Financial, and Paine Webber.
A comparable firm should be one with a similar risk profile as the firm in question. The internet firms are very different from Ameritrade. They obtain most of their revenue through advertisements, whereas Ameritrade obtains 68% of its revenue from the discount brokerage. These companies do not obtain any revenue from the discount brokerage. Hence, they are not suitable for this purpose. Investment service companies obtain some of their revenue from the discount brokerage. However, the proportion of discount brokerage revenue as compared to other revenue sources is small. In some cases, it is as low as 12%. This fact disqualifies them from being used as comparator firms.
The best group is the discount brokerage firms. They obtain the majority of their revenue from transaction fees just like Ameritrade. The only difference is the specific types of transactions. Therefore, it would be reasonable to assume that since they are in the same business, these forms are exposed to similar risks. I would therefore recommend these firms as the benchmark for the planned investments.
Computation of Asset Betas for comparative companies
Using the SLOPE function in excel, carry out a regression analysis on each of the company’s returns and the VW NYSE. The result is the equity beta for each company.
Computation of Ameritrade’s cost of capital using CAPM
Ameritrade should use an estimated cost of capital of 22%. This is computed in the following way:
Estimated Risk-Free Rate = 6.61%.
Estimated market Risk Premium = 7.2%.
Estimated Asset Beta = 2.069.
Expected Asset Return = 6.61% + (2.069 * 7.2) =21.509%.