Introduction
This paper considers the model of an ideal gas and its implementation on the example of an experiment on changing the volume of a gas cylinder and the corresponding dynamics of temperature and pressure. Experimental primary data are presented in the form of graphs of the corresponding dependencies in the time period. As a result, it was found that the volume is indeed directly proportional to the temperature and inversely proportional to the pressure in the gas cylinder.
Data
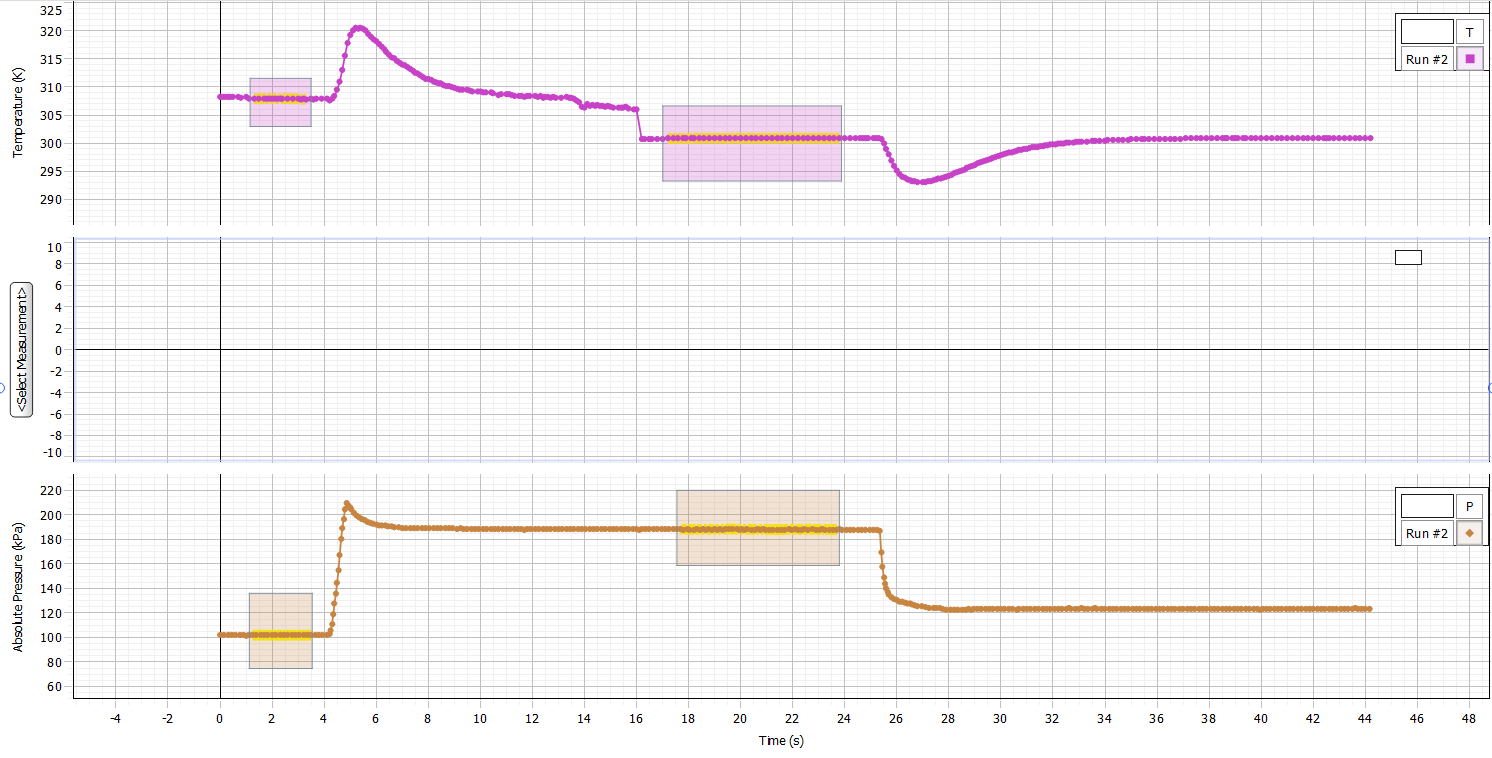
The data was collected using the Capstone software.
The uncertainties in this work lie in the syringe calibration, which does not initially take into account the volume of air in the tube. However, this error is eliminated by introducing the variable V0, which can be calculated algebraically.
Results
Calculations at constant temperature turned out to be inconsistent in the case of this experiment, which forces us to resort to the introduction of V0.
Accordingly, now the initial volume and the second one look like:
Therefore, the ratios can now be calculated using the formula and compared as a percentage:
Analysis
When the balloon is compressed, the pressure rises sharply by more than a factor of two for a short period of time due to the corresponding sudden rise in gas temperature. As soon as the temperature decreases, the pressure decreases and becomes constant.
The pressure does not return to its original value due to the decrease in volume, although at the same time the molar amount of gas remains the same.
When the pressure is released, the temperature drops sharply or drops, but then returns to room temperature. This happens due to sudden decompression, which is inherently adiabatic (Woody, 2018). In fact, the indicator returns to this value due to the heat flow from the environment into the syringe.
The need to introduce the indicator V0 is dictated by the inconsistency of temperature. At the same time, in various laboratory settings, this indicator can differ by a value of approximately 1 cubic centimeter, which makes this uncertainty significant at first glance. However, in fact, in this situation, work is carried out with a sufficiently large volume of gas from 40 to 60 cubic centimeters, which allows us to consider this uncertainty not relative, but absolute.
Accordingly, we can conclude that the model of an ideal gas, taking into account all potential errors, gives reasonable and close values for predicting the behavior of the gas. In this case, the following assumptions remain valid that all molecules are interchangeable, their type and mass are not taken into account in influencing the behavior of the gas; electric and gravitational forces between them are also leveled due to the large distance. Finally, only elastic collisions of molecules are taken into account, which is explained by the processes above. The response time of half a second just gives an increase and a longer decrease in the values to the equilibrium, which is noticeable from the work schedule.
Conclusion
This installation, using the ideal gas model, really made it possible to verify experimentally that it gives reasonable predictions of gas behavior. Minor deviations are explained by the physical processes of decompression, taking into account the molar amount of gas with the dynamics of volume and temperature.
Reference
Woody, A. I. (2018). How is the ideal gas law explanatory?. Science & Education, 22(7), 1563-1580.