The Bank’s maturity gap
Maturity gap of the bank (MGAP) = Maturity of assets (MA) – Maturity of liabilities (ML). Maturity of assets (MA) = [0*15+ (6/12)*120 + 3*100+ 5*220 +5*400 + 5*150 + 10*260 +10*530+ 15*200+ 20*150+ 20*320]/ (2405- 20) = 24,510/2385 =10.28 years
Maturity of liabilities (ML) = [0*125+ 0*42 + (3/12)*215+ (6/12)*180 +1*460 + 2*150 + 5*250 +20*200+ 0*200+ 3*300]/ (2405- 363) = 7053.75/2042= 3.45 years
Maturity gap (MGAP) = 10.28 – 3.45 = 6.83 years.
The bank’s repricing gap when the planning period is 1 year and 2 years
Both cash and equipment are noninterest earning assets (Choudhry, 2011).
Repricing gap (RP) = Rate sensitive assets (RSA) – Rate sensitive liabilities (RSL)
When the planning period is one year, the repricing gap = RSA – RSL= 6 month T-bills (4.25%) + 5 year personal loan (11.5%, repriced @ yearly) + 10 year commercial loan (12.25% repriced @ 6 months) + 15-year commercial loan at fixed 10% interest (repriced monthly) -3 months CDs (3.8%) – 6 months CDs (3.85%) – 1 year term deposit (4.0%)- overnight repo (3.4%) = $120+ 400 +530 +200 – (215+180+460+200) = $195 million.
When the planning period is two years, the repricing gap = RSA – RSL= 6 month T-bills (4.25%) + 5 year personal loan (11.5%, repriced @ yearly) + 10 year commercial loan (12.25% repriced @ 6 months) + 15-year commercial loan at fixed 10% interest (repriced monthly) -3 months CDs (3.8%) – 6 months CDs (3.85%) – 1 year term deposit (4.0%)- 2 year term deposits (4.3%)+ overnight repo (3.4%) = $120+ 400 +530 +200 – (215+180+460+150+200) = $45 million.
The bank’s duration gap when the current market yield was flat at 6.5%
Weighted average bank assets duration (DA)
Whereby Wi is the market value of asset I divided by all bank assets market value (Grier 2007, p.70).
Da = Macaulay’s asset I duration
n= is the different bank assets number
Therefore, the weighted market values of the following assets are computed as follows:
6 months T-bills (6.5%) duration = (Asset value/Total market value of assets) X duration of the T-bills. Duration = (120/2385) X 0.5 =0.025 years
3 year T-notes (6.5%) duration = (Asset value/Total market value of assets) X duration of the T-notes. Duration = (100/2385) X 3 =0.126 years
5 year T-notes (6.5%) duration = (Asset value/Total market value of assets) X duration of the T-notes. Duration = (220/2385) X 5 =0.461 years
5-year personal loan (6.5%) duration = (Asset value/Total market value of assets) X duration of the personal loan. Duration = (400/2385) X 5 =0.839 years
5-year Kangaroo bond (6.5%) duration = (Asset value/Total market value of assets) X duration of the Kangaroo bond. Duration = (150/2385) X 5 =0.315 years
10 year car loans (6.5%) duration = (Asset value/Total market value of assets) X duration of the 10 year car loan. Duration = (260/2385) X 10 =1.090 years
10-year commercial loan (6.5%) duration = (Asset value/Total market value of assets) X duration of the 10-year commercial loan. Duration = (530/2385) X 10 =2.222 years
15-year commercial loan (6.5%) duration = (Asset value/Total market value of assets) X duration of the 15-year commercial loan. Duration = (200/2385) X 15 =1.258 years
20-year Kangaroo sovereign bonds (6.5%) duration = (Asset value/Total market value of assets) X duration of the 20-year Kangaroo sovereign bonds. Duration = (150/2385) X 20 =1.258 years.
A 20-year mortgage at 6.5% interest, balloon payment, duration = (Asset value/Total market value of assets) X duration of the 20-year mortgage at 6.5% interest, balloon payment. Duration = (320/2385) X 20 =2.683 years.
The weighted average bank assets duration (DA) = 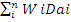
= 0.025 + 0.126 +0.461+ 0.839+ 0.315+ 1.090+ 2.222+ 1.258+ 1.258+ 2.683 =10.274 years.
Conversely, the weighted Average Bank Liabilities Duration (DL) = 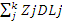
Whereby:
zj = Market value of liability j divided by all bank liabilities market value
DLj= Macaulay’s liability j duration
k = different bank liabilities number.
The weighted market values of the following liabilities are computed as follows:
3 months CDs (6.5%), duration = (Liability market value/Total market value of liabilities) X duration of the 3 months CDs. Duration = (215/2042) X 0.25 =0.026 years
6 months CDs (6.5%), duration = (Liability market value/Total market value of liabilities) X duration of the 6 months CDs. Duration = (180/2042) X 0.5 =0.044 years.
1-year term deposit (6.5%), duration = (Liability market value/Total market value of liabilities) X duration of the 1-year term deposit. Duration = (460/2042) X 1 =0.225 years.
2-year term deposit (6.5%), duration = (Liability market value/Total market value of liabilities) X duration of the 2-year term deposit. Duration = (150/2042) X 2 =0.147 years
5 year CDs at 6.5% interest balloon payment, duration = (Liability market value/Total market value of liabilities) X duration of the 5 year CDs at 6.5% interest balloon payment. Duration = (250/2042) X 5 =0.612 years
20-year debentures at 6.5% interest, balloon payment, duration = (Liability market value/Total market value of liabilities) X duration of the 20-year debentures at 6.5% interest, balloon payment. Duration = (200/2042) X 20 =1.959 years
Overnight repo at 6.5% interest, duration = (Liability market value/Total market value of liabilities) X duration of the Overnight repo. Duration = (200/2042) X 0.002 =0.0003years
The weighted average bank assets duration (DA) = 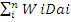
= 0.026+ 0.044+ 0.225+ 0.147+ 0.612+ 1.959+ 0.0003 =3.0133 years.
The duration gap of the bank assuming the current market yield is flat at 6.5% is given by DGA = Da – WDL.
DGAP is the duration gap
Da represents the average duration of assets
DL is the average duration of liabilities
W is the ratio of total liabilities to total assets.
Therefore, DGAP = 10.274 – (2042/2385) (3.0133) = 10.274 – 2.5799 = 7.694 years
The impact on net interest income over the next six months when current market interest is 5.65%
If the current interest rate of the market is 5.65%, then a decrease in bank sensitive assets by 50 basis points causes a change in the asset sensitive interest rate to decrease from 5.65% by 0.5% to 5.60%. On the other hand, a decrease in the rate-sensitive liabilities by 25 basis points causes the interest rate of these liabilities to decrease by 0.25% to 5.40%. Therefore, in the next six months, the bank’s funding gap will be:
Repricing gap (RP) = Rate sensitive assets (RSA) – Rate sensitive liabilities (RSL) (Choudhry, 2011). Re-pricing or funding gap using six months planning period will incorporate 6 month T-bills. (4.25%) + 10 year commercial loan (12.25% repriced @ 6 months) + 15-year commercial loan at fixed 10% interest (repriced monthly) -3 months CDs (3.8%) – 6 months CDs (3.85%) – overnight repo (3.4%) = $120+ 530 +200 – (215+180+ 200) = $255 million.
From the six months funding gap, a decrease of 0.5% in asset sensitive rate, and a 0.25% decrease in liabilities sensitive rate causes the net interest income to decline by $2.76 million. NII = FG(R) = [$120+ 530 +200] x0.005 – (215+180+ 200) x0.0025 = $2.76 million.
The impacts of the anticipated short-term deposits on the overall asset-liability of the bank
Short-term deposits pay low interests to the bank as compared to long-term deposits. This means that short-term deposits are associated with high-interest expense especially on short-term liabilities such as CDs. Hence if the bank relies heavily on CDs it has to pay higher rates since these short-term non-core liabilities are riskier. Moreover, the maturity gap for asset-liability of the bank will widen as clients resort to short-term deposits.
The reason being the bank will increase its long-term lending capacity while borrowing for the short-term (Choudhry & Masek 2011). The effect is that in the short-term interest rates will rise thus increasing the borrowing cost of the bank. Furthermore, excessive short-term deposits have short re-pricing periods that omit exposure of assets-liability to the risk associated with interest rates. Therefore, short-term deposits will understate the balance sheet’s rate sensitivity.
The impact on equity when interest rate increases by 50 basis points across the yield curve
When the bank anticipates that the interest rate will increase across the yield curve by 50 basis points, such an increase will cause the equity value to decrease. The value of the equity will be lowered because when the interest rate increases by 0.5%, it reduces both the liabilities and assets market values. However, the bank’s assets market value tends to decline more than the liabilities market value given that the duration of the asset is longer than the bank’s liabilities duration (Choudhry, 2003).
Strategies to reduce the equity value volatility
Several approaches can be used to reduce volatilities on valued assets. One of the approaches is based on asset allocation. This is where the assets are tactically allocated to generally reduce the portfolio volatility. The equity is allocated at the right time depending on the rewards or risks that are expected for a range of asset classes. Though timing the market might be a challenge it should be given greater consideration to enhance its achievements (Ghosh, 2012).
The other approach is the use of derivatives. The bank may use Derivatives to purchase the portfolio insurance as a cushion against the pending losses. In other words, this strategy is inclined to reduce volatility by holding another class of assets whose value is likely to increase while the value of other equities is falling. However serious considerations should be taken on the cots that are involved resulting in the reduction of long-term returns.
The other strategy is diversification in various emerging equity markets. Diversification improves the overall portfolio efficiency while at the same time reduces the risk. However, the assets are still exposed to the overall equity risk premium (Choudhry, 2003). Also, geographic diversification will safeguard the bank’s portfolio against some eminent unrelenting losses which will probably ensue within a particular equity market range. Other strategies such as value or income and low volatility equity may also be applied to reduce volatility in assets.
The bank’s liquid capital sufficiency to meet the Basle II requirement
Generally, Basle II requires that banks and other financial institutions hold a greater amount of capital that can be used to militate against the risks that these institutions may be exposed to. According to the requirement, this bank holds enough capital in form of portfolios and equity that can be used to safeguard against the risks that the bank may be exposed to (Choudhry & Masek, 2011). The amount of equity and assets more so the liquid assets that the bank hold is enough to settle any eventuality that may arise as a result of operational and lending practices.
The development of credit risk management
Introduction
Credit risk management has dramatically evolved over the last twenty years as a result of secular forces that have increased the importance of its measurements. These forces that have driven the development of credit risk management includes the structural rise in the number of worldwide bankruptcies, the widening disinter-mediation trend by the largest and highest quality borrowers, increased competition on loan margins, the real asset declining value in various markets, and increased growth in instruments of the statement of affairs having intrinsic risk exposure default (Altman & Saunders 1998, p.171).
Banking professionals responded to these challenges through the development of new and sophisticated models that comprise credit-scoring and early warning systems. Moreover, the banking industry moved away from individual loans and securities risk analysis to the adoption of the fixed income securities measurement of portfolio risk where the credit risk assessment plays a vital role (Altman & Saunders 1998, p.171). Models such as the risk-adjusted-return on capital (RAROC) were developed (Altman & Saunders 1998, p.171). Such sophisticated models were developed to better measure the credit risks of off-balance sheet instruments.
Traditional credit measurement methods
One of the early credit measurement methods that most financial institutions virtually relied upon to assess loans was the subject analysis or expert system. In this system bankers relied upon the information on the borrower’s characteristics such as its reputations, collateral, leverage as well as the volatility of its earnings to arrive at their credit decisions (Altman & Saunders 1998, p.172). Such decisions were largely subjective or expert. However, this system of credit measurement have largely been outperformed by other more objective methods of credit measurement such as the multivariate credit-scoring system
In the multivariate scoring system or the accounting-based credit-scoring system, the financial institutions make decisions by making comparisons of potential borrowers’ various key accounting ratios with that of the group or industry (Altman & Saunders 1998, p.172). In the model, vital accounting variables are added and weighted to give either the credit-risk score or the probability of risk default measures. In case the value attained by the credit- risk score or probability is above the required benchmark, then the credit applicant is either subjected to further scrutiny or rejected.
Newly proposed models
The resultant weaknesses in the traditional methods led to the development of new models to replace the traditional bankruptcy prediction and credit-scoring models. The most recent models include the KVM. In this model, crucial inputs into the probability of default have to be estimated. The model is based on the concepts of option pricing model whereby the asset value of the firm is evaluated as the firm’s equity value call option (Altman & Saunders 1998, p.174). Secondly, the model is founded on the theoretical linkage amid the firm’s equity value observable volatility and its asset value unobservable volatility.
The second newer approach backed with stronger theoretical underpinnings is those models that accredit the disguised likelihood of the term structure default of yield spreads amid risky corporate and default-free securities. The models draw from the disguised forward rates on risky bonds and risk-free as well as the utilization of these rates to pull out the default market expectations at prospective variant periods (Gordy 2000, p.124).
The models operate under various assumptions such as that the expectations of interest rates theory holds, that there is reduced transaction cost, that there is the absence of call sinking fund together with other optional features, and that there is the existence of discount-bond yield-curves and such curve can be extracted from coupon-bearing yield-curves (Gordy 2000, p.126).
The third newer model is the capital market-based. These models are based on the mortality rate model and the aging approach. This approach is currently being applied in the structured financial instruments analysis and can be extended to the analysis of default loans (Altman 1984, p.177). The fourth new model applies the neural network analysis on the problems of credit risk classifications. In particular, the neural network credit risk model examines potentially hidden relationships between the predictive variables which are then utilized as additional explanatory variables in the non-linear bankruptcy prediction function.
In conclusion, these credit risk measures have various disadvantages that render them inapplicable in some situations. That is, each model cannot be exclusively applied in the credit risk analysis. The first traditional subjective analysis was found to be inadequate as the number of credit risk in LDCs increases hence, outperformed by multivariate credit scoring systems. Besides, the multivariate credit scoring models have been criticized for being overly based on the book value accounting data which is measured at discrete intervals. The effect of this is that the model fails to pick the more subtle and fast-moving changes in borrower conditions.
Secondly, its linearity assumption is flawed and the model is further based on the tenuously underlying theoretical models. Other newer models such as the KVM have been criticized over the inaccuracy of using the stock prices to derive the implied or expected variability in the values of assets. This makes the assumptions used in these models to be questionable.
References
Altman, E & Saunders, A 1998, “Credit risk measurement: Developments over the last 20 years”, Journal of Banking and Finance, vol.21 no.11-12, pp. 1721-1742.
Altman, E 1984, “The success of business failure prediction models: An international survey”, Journal of Banking and Finance, vol.8 no.2, pp. 171-198.
Choudhry, M & Masek, O 2011, An introduction to banking: liquidity risk and asset-liability management, John Wiley & Sons, Hoboken.
Choudhry, M 2003, Bond and money markets: Strategy, trading, analysis, Butterworth-Heinemann, Oxford, UK.
Choudhry, M 2011, Bank asset and liability management: strategy, trading, analysis, John Wiley & Sons, Hoboken.
Ghosh, A 2012, Managing Risks in Commercial and Retail Banking, John Wiley & Sons, Hoboken, New Jersey.
Gordy, M 2000, “A comparative anatomy of credit risk models”, Journal of Banking and Finance, vol.24 no.1-2, pp. 119-149.
Grier, WA 2007, Credit analysis of financial institutions, Euromoney Books, New York.