Big O Notation is a method used to describe time and space that are required for conducting an algorithm. Thus, this method is used when it is necessary to measure and clarify how the number of operations in an algorithm can scale as a function depending on changes in the input (Christian & Griffiths, 2016). Big O Notation is helpful to explain the behavior of algorithms with reference to changes in the size of specific input data. As a result, the use of Big O Notation allows for classifying behaviors of algorithms with the focus on time and space categories, or time and space complexity (Time complexity is the amount of time required for an algorithm, and space complexity is the amount of space required for a specific algorithm (Gregoire, 2014)). The examples of Big O Notation may be provided with the focus on the time complexity or the runtime of algorithms as this category is most actively measured and described by scientists (VanderPlas, 2016). Therefore, the key question that can be answered with the help of Big O Notation is the following one: how much slower or faster can a certain algorithm run if more data are added (for instance, 10,000 items instead of 1)?
If a person wants to predict and describe changes in resource needs depending on the growth of the input data, he or she applies Big O Notation for a selected algorithm. For example, while developing a rating and using an appropriate algorithm, it is important to know how this algorithm will work during the worst-case scenario when the involved data becomes significantly bigger and how much time will be required. The use of Big O Notation will help to describe specific resource needs depending on increases in the data important for creating a rating system.
This type of formal notational approaches is known as an asymptotic notation. It is important to pay attention to the fact that this specific method was proposed by Paul Bachmann in 1892, and it was described by the mathematician and theorist in his Analytic Number Theory. This approach was also developed by Edmund Landau, and Big O Notation is also known today as the Bachmann–Landau notation (Christian & Griffiths, 2016; VanderPlas, 2016). Thus, the notation became actively used in science in the 19th century.
There are four common behavior types that are associated with Big O Notation:
- constant;
- linear;
- logarithmic;
- quadratic.
In spite of the fact that there are more behavior types, these four algorithms are mostly used by scientists and programmers in their practice. These behaviors need to be discussed in detail:
- Constant (O (1)): In this behavior, the runtime of an algorithm does not depend on the number of elements. The same time will be required for an algorithm in spite of the amount of input data (VanderPlas, 2016). For example, this behavior can be used in order to assess a single action in relation to the group of elements in one array.
- Linear (O (n)): In this behavior, the runtime increases in accordance with the growth of elements (Christian & Griffiths, 2016). Thus, when the input doubles, the runtime will also double. This behavior can be applied to searching for particular elements in unsorted lists or to completing ratings.
- Logarithmic (O (log n)): In this behavior, the runtime grows logarithmically (Gregoire, 2014). For instance, if it is necessary to find one element in an unsorted array using a binary search approach, this algorithm can be applied.
- Quadratic (O (n2)): In this behavior, the runtime tends to grow quadratically, depending on the number of elements (Christian & Griffiths, 2016; VanderPlas, 2016). The running time related to the selected algorithm will be limited by a specific quadratic function of n in this case. This algorithm can be viewed as slower in comparison to linear and logarithmic behaviors of Big O Notation.
These four typical Big O Notation behaviors demonstrate how much time or space a specific algorithm can take if the number of data elements or the input increases according to one of the behavior types. For example, if a linear algorithm is used (O (n)), it is possible to determine the amount of time required for an algorithm when the amount of data grows. If the O (n) algorithm takes approximately 1 minute to operate when n = 100, then it will take roughly 6 minutes when n = 600.
However, Big O Notation is not a method that represents the particular amount of time required for a selected algorithm, and the notation does not provide an exact answer to the question about the number of minutes required to conduct an algorithm. On the contrary, Big O Notation is a method that represents a function, which demonstrates changes in scaling when the number of elements changes (Christian & Griffiths, 2016; VanderPlas, 2016). The presentation of Big O Notation behaviors in the form of functions is actively used to answer the question about time and space complexity related to a selected algorithm (Figure 1).
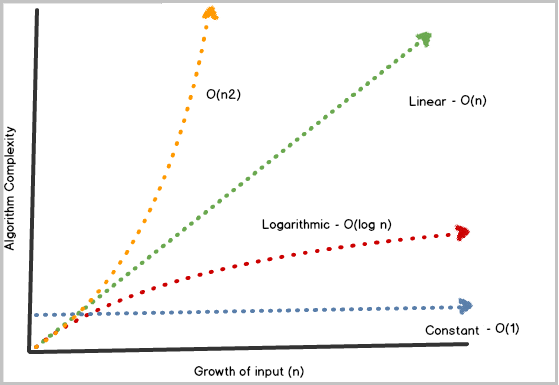
Big O Notation is actively used in computer science, but it should be distinguished from little–o notations, big-Ω notations, and big-Θ notations. In contrast to little–o, big-Ω, and big-Θ notations, Big O Notation can be used in the majority of cases without modifying the context and certain conditions (Christian & Griffiths, 2016; VanderPlas, 2016). While comparing Big O Notation and little–o, big-Ω, and big-Θ notations, it is possible to state that Big O Notation is an easier method than the other types of asymptotic notations (Gregoire, 2014). Furthermore, different behaviors and formal algorithms associated with Big O Notation allow for avoiding the use of any other complex notation. As a result, this method is actively utilized in cases when it is necessary to compare the performance of different algorithms with reference to a certain number of data elements in order to select the most appropriate one.
When Big O Notation is used, scientists determine specific prerequisites and conditions of algorithms to design the most efficient ones that can be applied to a project and demonstrate a curve for the selected function. From this perspective, Big O Notation is often defined as a measure that accentuates the relative performance in contrast to the absolute one. Therefore, it is impossible to determine the actual amount of time required to take an algorithm. Finally, it is important to note that Big O Notation can be applied only to those specific algorithms where the rapidity of the process directly depends on the used amount of data. This notion cannot be applied to those algorithms, in which no input is identified or time can be random.
References
Algorithms data structures [Image]. (n.d.). Web.
Christian, B., & Griffiths, T. (2016). Algorithms to live by: The computer science of human decisions. New York, NY: Macmillan.
Gregoire, M. (2014). Professional C++ (3rd ed.). Indianapolis, IN: John Wiley & Sons.
VanderPlas, J. (2016). Python data science handbook: Essential tools for working with data. Sebastopol, CA: O’Reilly Media.