Explanation of the Five-Factor Model
Table 1 below shows regression statistics, which describes the nature of the regression model (the five-factor model).
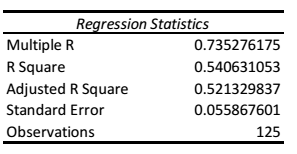
From the table, the coefficient of multiple correlation (R) is an important value, which depicts the nature and degree of association that independent variables and dependent variable exhibit. In this case, the five-factor regression model has a high positive correlation (0.735). The coefficient of multiple correlation has a value, which ranges from zero to one. The coefficient of multiple correlation of one means that the independent variables powerfully predict a dependent variable, while the coefficient of multiple correlation of zero means that independent variables do not predict the dependent variable. In this view, the high positive correlation implies that the combination of SFR, LT20, GT50, GRAD, and FRR strongly predicts alumni donations.
The table also has a coefficient of determination called R-square (R2), which explains how analyzed data fit the multiple regression model. R-square emanates from the square of R, the coefficient of multiple correlation. In this case, the square of 0.735 gives a value of 0.54, which is the coefficient of determination. R-square takes a value that ranges from zero to one in that zero indicates no explanatory power and one shows high explanatory power. For purposes of explanation, R-square value is converted to a percentage figure to enhance clarity and description of the explanatory power. The R-square value of 0.54 implies that all the independent variables in the model, namely, SFR, LT20, GT50, GRAD, and FRR, explain 54% of the variation in alumni donations. Given that the independent variables have an individual contribution to the model, the combined contribution shows that 54% of the overall variation in the dependent variable occurs due to the independent variables in the model. Specifically, SFR, LT20, GT50, GRAD, and FRR contribute to 54% of the variation in alumni donations while 46% remains unexplained. In essence, the explanatory power of 54% means that SFR, LT20, GT50, GRAD, and FRR moderately explain alumni donations.
Given that the multiple regression model may contain insignificant predictors, which do not contribute to the model, the coefficient of determination requires adjustment to penalize these predictors. The adjusted R-square is 0.52, which means that the independent variables, SFR, LT20, GT50, GRAD, and FRR, explain 52% of the variation in alumni donations. Like R-square, adjusted R-square takes values that range from zero to one. In this view, the adjusted R-square has a moderate explanatory power, which implies that SFR, LT20, GT50, GRAD, and FRR moderately explain alumni donations. Given that the difference between R-square and adjusted R-square is 0.02, it suggests that insignificant predictors only explain 2% of the variation in alumni donations. In this view, the contributions of insignificant predictors are negligible to warrant their exclusion from the model. Therefore, the adjusted R-square shows that SFR, LT20, GT50, GRAD, and FRR are significant predictors of alumni donations, and thus, the data fit the multiple regression model.
In the regression statistics table, the standard error is a central value in the interpretation of the multiple regression model. The standard error measures the precision of predictions, namely, R, R-square, and adjusted R-square. Given that R prediction indicates that there is a high positive correlation between the independent variables and the dependent variable, the presence of the influential outliers is unknown. Moreover, R-square and adjusted R-square show a moderate explanatory power of independent variables, but they do not indicate the existence of influential outliers. Hence, the standard error is essential because it explains the variation of data points in the multiple regression model. In this case, the standard error is 0.056, which shows that the average variation of data points in the multiple regression model is 5.6%. Therefore, the average variation explains 5.6% of the variability of data points in the multiple regression line, which indicates the goodness of fit.

To determine if the multiple regression model is significant, interpretation of the ANOVA table (Table 2) is essential because it presents F-ratio. From the table, it is evident that the multiple regression model is statistically significant, F(4, 95) = 28.01, p < 0.05. The ANOVA table denotes that the independent variables, namely, SFR, LT20, GT50, GRAD, and FRR are statistically significant predictors of alumni donations. In this view, it confirms that the multiple regression model is a good fit for the data analyzed. In essence, the multiple regression model significantly predicts the relationships between SFR, LT20, GT50, GRAD, and FRR, and alumni donations.
Statistically Significant Factor
Analysis of the individual independent variables indicates that they have different predictive impacts on the dependent variable. Specifically, predictive effects of SFR, LT20, GT50, GRAD, and FRR vary in that one is a significant predictor, while others are insignificant predictors.

From Table 3, it is apparent that LT20 is an independent variable, which has a significant association with alumni donations, the dependent variable. Since the p-value of LT20 is 0.017, it is less than the significance level of 0.05, and thus, it means that LT20 is a significant predictor of alumni donations. Reading from the table, LT20 has a positive coefficient, which indicates that its increase causes an increase in the alumni donations. Precisely, the ratio indicates that a unit increase in LT20 leads to 0.152 an increase in alumni donations when all other independent variables are constant.
The interpretation of data should not discount variables that are not statistically significant because they give a substantial contribution to the model based on the multiple regression model. The insignificant variables are SFR, GT50, GRAD, and FRR because their p-values are greater than 0.05. In assessing the influence of individual independent variables on the dependent variables, p-values are applicable in determining the degree of influence. Independent variables with p-values less than 0.05 are significant predictors while independent variables with p-value more than 0.05 are insignificant predictors. Despite the fact that these variables are insignificant predictors of alumni donations, the multiple regression model should not discount them in the prediction of alumni donations because they have some undefined contributions to the model. Hence, as the multiple regression model provides a good fit for the data, it is statistically sensible not to discount the insignificant predictors.
Interpretation of Most Significant Factor Influencing Alumni Donations
Multiple regression analysis indicates that LT20 is the most significant factor influencing alumni donations. The significance of the LT20 emanates from the p-value, which is less than 0.05. LT20 and alumni donations have positive relationships, which imply that they both increase or decrease proportionately. The interpretation of the relationship is that a rise of LT20 by a unit results in an increase in alumni donations by 0.152 when all other independent variables remain constant. In this view, owing to statistical significance, LT20 is the only factor that significantly predicts the variation of alumni donation.
To plot the relationship between LT20 and alumni donations requires the use of coefficients in Table 3. A linear regression line has an equation, y = a + bx, which is applicable in predicting dependent variable and drawing scatter plot. In the equation, y is the dependent variable that is subject to the independent variable x. The multiple regression model has regression line with a gradient b and an intercept a. In this case, y is alumni donations, which is a function with an intercept of -0.197, a gradient of 0.152, and LT20 as a dependent variable. In essence, the linear regression equation is that:-
Alumni donations = -0.1971 + 0.1524LT20
Table 4 below shows derivatives of the regression equation and the respective values of LT20 and alumni donations, which are applicable in drawing the scatter.
Table 4.
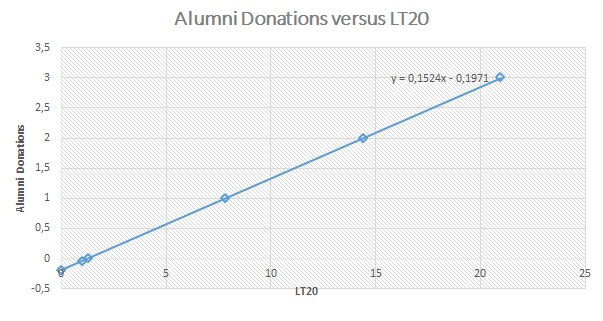
From the scatter plot, what is apparent is that LT20 and alumni donations have a positive correlation. The correlation implies that alumni donations rise as LT20 increases. In this view, the scatter plot of the regression model portrays LT20 as a significant predictor of alumni donations.
Given that LT20 is a statistically significant positive predictor of alumni donations, the College should utilize it effectively. Table 3 indicates that a unit increase in LT20 results in a significant rise in alumni donations by 0.1524. In this view, the College should focus on increasing LT20 for it to gain a significant increase in alumni donations. Although GRAD and FRR are not significant predictors of alumni donations, the College should increase them because they contribute to the prediction of the alumni donations. From their respective gradients, it is evident that a unit increase in each of these factors, GRAD and FRR, results in the rise of alumni donations by 0.128 and 0.260 respectively. In contrast, since some factors have a negative influence on the alumni donations, the College should minimize them. From Table 3, it is apparent that a unit increase in each of these factors, SFR and GT50, results in a decline of alumni donations by 0.001 and 0.034 respectively. The figures mean that the College needs to minimize their negative effects so that it can optimize the benefits of LT20, which boosts alumni donations. Overall, the College should increase alumni donations by increasing LT20, optimizing the influence of GRAD and FRR, and minimizing the influence of SFR and GT50.
Application of Information and Recommendations
To increase alumni donations in the long term, the College should leverage each of the independent variables because they have some influence on alumni donations. Regression statistics in Table 1 provides invaluable information about the multiple regression model. From the table, the coefficient of multiple correlation is very high, which denotes that the independent variables, SFR, LT20, GT50, GRAD, and FRR, have a high multiple correlation with alumni donations. The strength of multiple correlation provides a compelling support of the decision to leverage each of the independent variables in enhancing alumni donations. If the coefficient of multiple correlation had been less than 0.5, it would have implied that the correlation is moderate or weak, and thus, could be prone to influence of non-predictors. Hence, the coefficient of multiple correlation of 0.735 is high enough to support the decision to leverage each independent variable of the model, which determines alumni donations. The use of the coefficient of multiple correlation is realistic because it is a powerful predictor of the relationships among variables in the multiple regression model.
R-square is another important coefficient in the regression statistics table because it provides the percentage of variation in alumni donations that the independent variables collectively explain. In this case, SFR, LT20, GT50, GRAD, and FRR explain 54% of the variation in alumni donations. Critically, the explanatory power of the independent variables is sufficient to support the decision to leverage all the independent variables. Given that the existence of independent variables, which do not contribute to the model, reduces the explanatory power of these variables, the explanatory power of 54% is substantial. In this case, the explanatory power of 54% supports the decision to use all independent variables in increasing alumni donations in the long term. Evidently, it is realistic to apply the model to increase alumni donations because the explanatory power of 54% is moderate and has influential effects on alumni donations.
Adjusted R-square is an important coefficient of the regression analysis, which takes into consideration the effects of non-predictors in the model. The adjusted R square, in this case, is 0.52, and it suggests that the explanatory power of the real independent variables minus fake independent variables is 52%. Therefore, the explanatory power of 52% is weighty because it explains over half of the variation in alumni donations. The use of 52% as explanatory power is realistic in supporting the decision to leverage independent variables. The difference between R-square and adjusted R-square gives an invaluable information about the existence of noise in the independent variables. When the difference is large, it means that the model has many independent variables, which do not contribute to the model. When the difference is small, it implies that the model has no or minimal number of variables that do not contribute to the model. In this case, the difference of 0.02 indicates that the independent variables explain a noise of 2%, which does not predict alumni donations. Hence, the small difference between R-square and adjusted R-square support the decision to leverage all independent variables with a view of optimizing alumni donations.
From the regression statistics table, standard error supports the decision of leveraging all independent variables. The standard error indicates that the model is accurate in predicting alumni donations because it shows that there are no significant outliers, which could disrupt or distort the regression equation. Essentially, the standard error shows that the mean variation of the data points in the multiple regression model is 0.056, which implies that the mean variation explains 5.6% of the variability in data points. The standard error indicates that outliers do not cause a considerable influence on the model, and hence, the model is accurate and precise in predicting alumni donations. In this case, it is recommendable to use the model in predicting alumni donations using the independent variables because the standard error is negligible to have an influential impact on the model.
Table 1 indicates that the multiple coefficient of correlation is high, R-square is moderate, adjusted R-square is stable, and the standard error is negligible, and thus, supports the use of the model in predicting alumni donations. Fundamentally, the preliminary multiple regression analysis supports the decision of leveraging all independent variables in increasing alumni donations. The ANOVA table provides compelling evidence, which support the decision of leveraging independent variables because the multiple regression model is statistically significant, F(4, 95) = 28.01, p < 0.001. The p-value of less than 0.001 implies that the model is statistically significant with virtually no chance of random occurrence. Therefore, the analysis recommends the College to employ the multiple regression model in predicting alumni donations because the independent variables collectively have a statistically significant contribution to the model.
Since individual independent variables contribute to the model, regression analysis of each of them gives the importance of their contribution. Table 3, which contain coefficients of each variable, indicate that LT20 is an independent variable that has the most influential impact on alumni donations and is statistically significant. The p-value of LT20 is 0.017, which is less than the significance level of 0.05, and thus, making it a very noteworthy predictor of alumni donations. LT20 has a coefficient of 0.1524, which designates a positive correlation with alumni donations. Moreover, the coefficient means that for every unit increase in LT20, alumni donations increase by 0.1524 when all other independent variables are constant. The scatterplot depicts the relationship of the LT20 and alumni donations, and thus, supports the increment of LT20 as a robust predictor of alumni donations. In this view, the interpretation of data recommends the College to concentrate on augmenting LT20 to increase alumni donations for it is a significant predictor of alumni donations.
The College should also consider GRAD, FRR, SFR, and GT50 in increasing alumni donations because they have a substantial contribution to the model. GRAD and FRR are two independent variables, which have a positive correlation with alumni donations, but they are statistically significant predictors. The interpretation shows that a unit increase in GRAD and FRR leads to a decrease in alumni donations by 0.128 and 0.260 respectively. Contrastingly, SFR and GT50 are two independent variables, which have negative impacts on the alumni donations. The interpretation shows that a unit increase in SFR and GT50 leads to a decrease in alumni donations by 0.001 and 0.034 respectively. The correlation values mean that the College should maximize GRAD and FRR because they have a positive correlation and minimize SFR and GT50 because they have a negative correlation with alumni donations. These recommendations are realistic because they have their basis on statistical figures and regression model. The College needs to leverage variables that are statistically insignificant because they contribute to the model.
Since GRAD, FRR, SFR, and GT50 are statistically significant predictors of alumni donations, they collectively have a statistically significant contribution to the model. Multiple regression analysis suggests that R, R-square, adjusted R-square, standard error, and F-statistic provide robust data, which support the inclusion and the use of all the independent variables in the prediction of alumni donations. These data are compelling because there is no additional information, which shows stepwise regression, backward elimination, and forward selection. The additional information would have indicated the fitness of different models, and thus, would have offered conclusive evidence regarding the optimization procedure of the model. In this view, the College should leverage independent variables to increase alumni donations.