Statement of the Problem
The primary research interest of this paper is the use of current financial capabilities to determine the practicality of purchasing an iPad Pro as the first visible goal. Buying this device is, in fact, a step toward achieving a more global dream, but fragmenting the overall goal into parts has been chosen to multiply the likelihood of achieving it. More specifically, the main problem is saving two thousand dollars but living comfortably and not suffering from a shortage of money. For this goal, I need to conduct a thorough personal budget analysis, identify funding channels, and identify actionable ways to accumulate this amount more quickly.
Problem Solving Model
Achieving this goal can be either spontaneous or systematic and organized. In the first case, I can use a no capital accumulation strategy and expect to have $2000 by myself, but it is clear that the risks of this approach are incredibly high. Therefore, systematic and structured strategies are my chosen strategies to achieve my goal. I will use a six-step solution model to solve the identified problem, as shown in Figure 1.
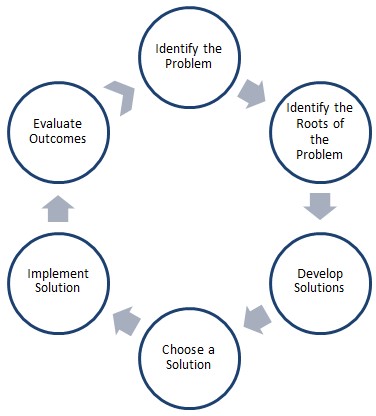
Since the problem has already been found, the next step is to establish the roots of the problem. A self-reflective analysis tells me that I want to save this money because I want an iPad Pro, which I will use for creativity. Therefore, the root of this problem is the desire to create and make drawings so that I can sell them and get money for them. This goal can be accomplished by alternative solutions, depending on time, difficulty, and desire. The main possibilities for accumulating funds consist of taking out a loan for this amount, saving with compound interest, investing in the stock market, and borrowing from my friends and relatives. Not every one of these decisions satisfies me or my moral expectations, so I choose to save using the compound interest model as the only proper solution. In this decision, however, I have to consider the fact that I need to regularly deposit some amount in a bank account to increase the time to reach my goal. However, the strategic point in this problem remains the calculation of that amount using mathematical models.
Mathematical Model
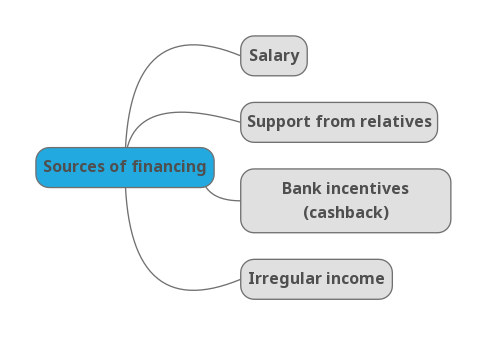
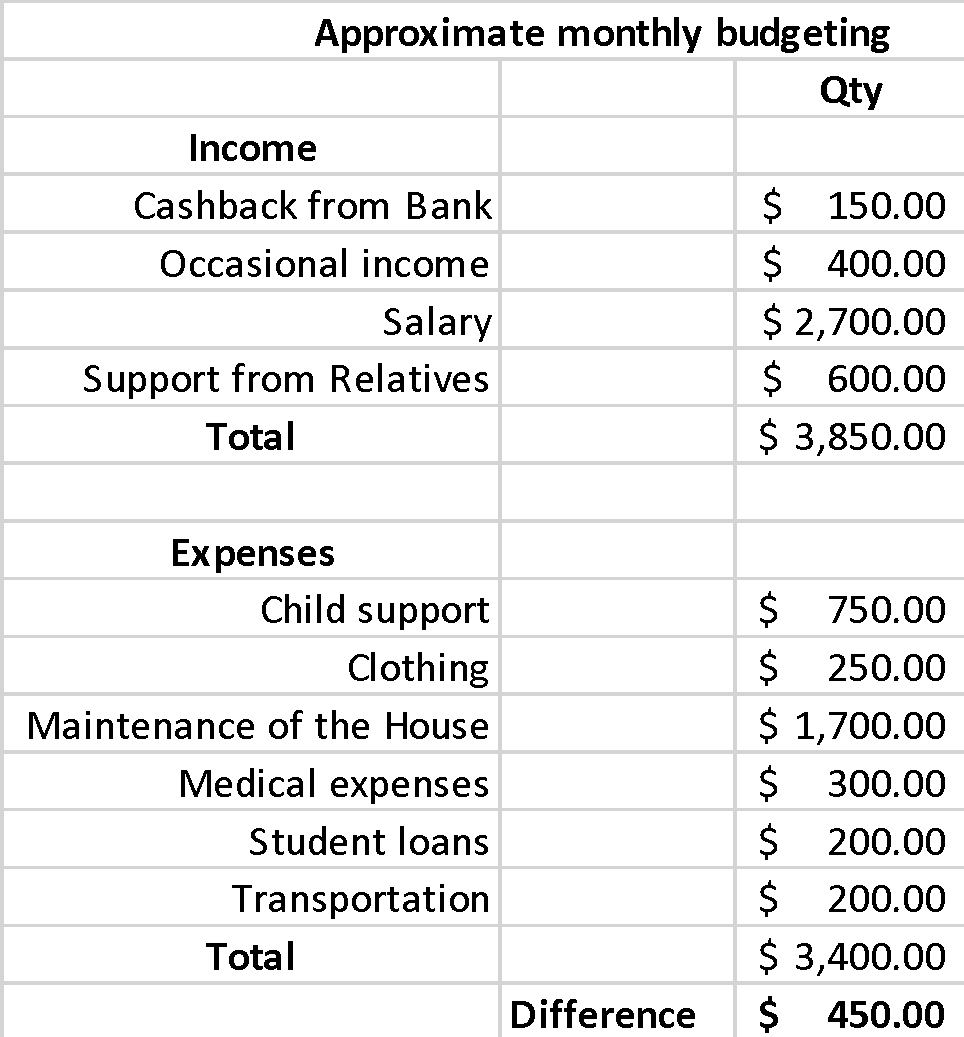
Based on personal feelings and using a spreadsheet, I have found that each month I have an unspent amount that I can invest. Specifically, this amount is about $400-$500 each month, while I may not save much on other expenses. Therefore, I am willing to invest about 30 percent to buy an iPad Pro using the compound interest method.
For compound interest, a well-known mathematical formula is used, which allows multiplying the equity by imposing interest on the added amount. It is well known that compound interest is a better investment strategy than simple interest because it shows exponential growth in the body of the deposit. The formula shown below is used to calculate compound interest investing, and I should know the interest rate r because I know all other data:
I use a value of 0.06 as the average U.S. bank deposit interest rate as the variable r (Goldberg, 2022). In other words, this is the annual percentage yield that local banks are willing to offer private investors like me. Compound interest will accrue on a quarterly basis, that is four times a year:
A=$152.08
Clearly, this is a necessary small amount, which is not even 10 percent of the final goal. This means that this strategy does not work, so I must account for the portion added at the beginning of each month so that my bank deposit works as a fixed deposit of the original amount. To do this, I constructed a spreadsheet, as shown in Figure 4. As you can see, in this case, I am accumulating up to $3.6K by the end of the second year, which is about one and a half times what I need. A closer look shows that the amount I needed was already accumulated 14 months after I started investing (Fig. 6). In other words, with the strategy used, I can not only significantly reduce the period of accumulation but also save up to $350 every month in free funds after deducting all expenses. Consequently, I can either follow the suggested way or reduce the amount of monthly deposit and have more free money every month, but it will increase the period of accumulation.

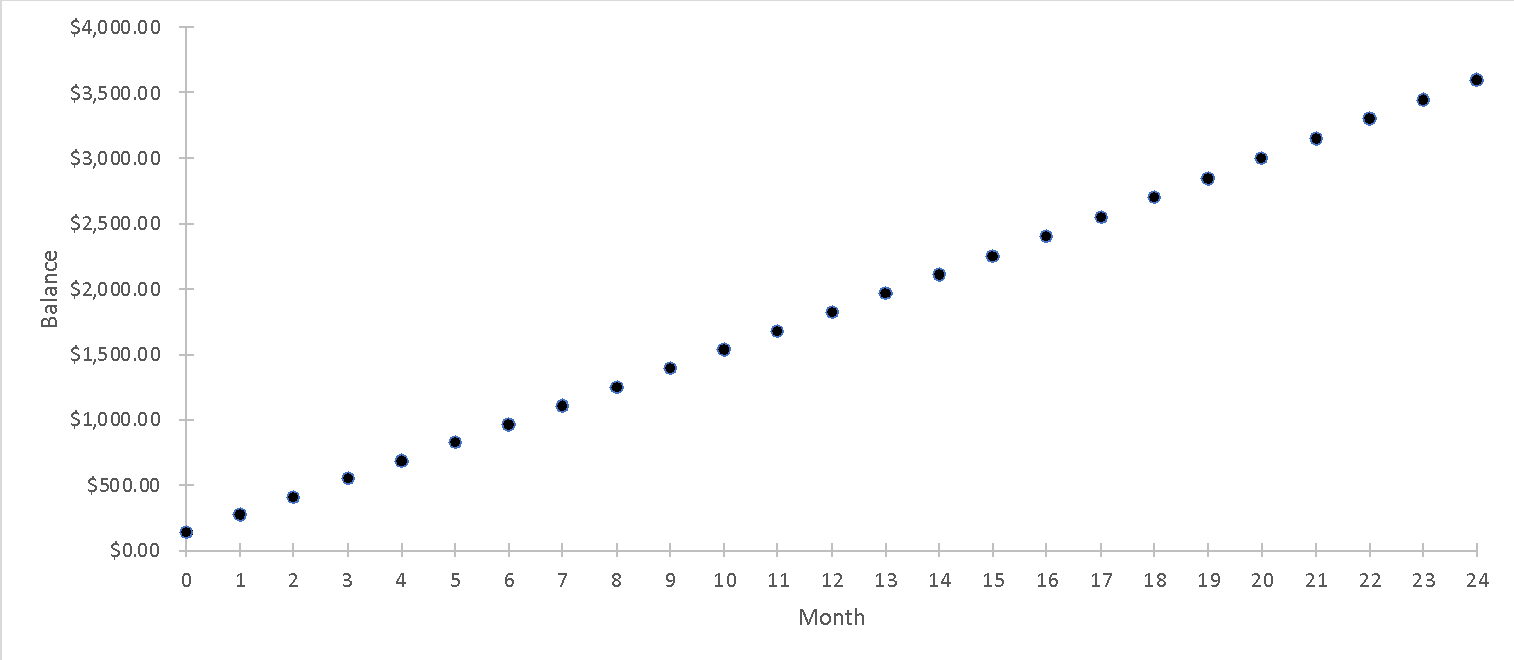
Summary
In the end, it is worth emphasizing that I was able to find a solution to my problem with the help of mathematical modeling. My expected time frame for achieving the goal was shortened, which is an overall advantage for me. With the decision-making model, I was able to fragment the overall goal and trace its realization at each step, allowing me to find and eliminate weaknesses. In this work, I had to measure the number of finances I could invest each month at compound interest, which I had not considered in my Week 7 proposal.
Reference
Goldberg, M. (2022). What is the average interest rate for savings accounts? Bankrate.