Introduction
In this laboratory work, we studied patterns of the centripetal motion of an object in a circle. In this type of motion, the object, during circular motion, experiences an equilibrium force pushing it toward the center of the circle. The centripetal force formula determines, Fc = (mv2)/R, that the value of this force is inversely proportional to the radius of the circle: that is, the further the object is from the center of the abstract circle, the less force it experiences (PHY, 2020). The formula also shows the dependence of the centripetal force on the angular velocity of the object and mass. The purpose of this paper is to conduct experiments to measure the radius (in m), free mass (in kg), and angular velocity (in m/s) as a function of the tension force of the string on which the object rotating in the circle is suspended.
Data and Analysis
In the present laboratory work, direct measurements were concerned with determining the value of radius (in meters), free mass (in kg), and angular velocity (in m/s) as functions of the tension force of the thread. Table 1 contains information on all three sections of the experiment. At first glance, several patterns can be noticed at once. First, it seems that the tension of the thread depends on the angular velocity of the suspended object, and as the angular velocity increases, the centripetal force also increases. Second, as the radius at which the object is suspended increases, the tension tends to decrease. Finally, as the free mass of the object increases, the tension also increases. It is also worth noting that the tension of the thread is the centripetal force, the patterns of which were evaluated in this paper.
Table 1. Data of direct measurements for the three experiments performed
For the measured data, it is possible to plot dependence plots, and these plots should be linearized. In particular, the graph of the dependence of the tension on the angular velocity does not reflect a linear dependence, so the values of the centripetal force were squared. This yielded a nearly linear trend for the relationship of this pair of variables, as shown in Figure 1. The linear regression shows that an increase in angular velocity for every one unit results in a 0.0019 unit increase in the square of the tension. This fully justifies the theoretical expectation that there is a direct proportionality between the square of the centripetal force and the angular velocity, namely Fc = (mv2)/R. The physical meaning of the y-intercept, in this case, is absent, because at zero velocity, no tension of the thread existed.
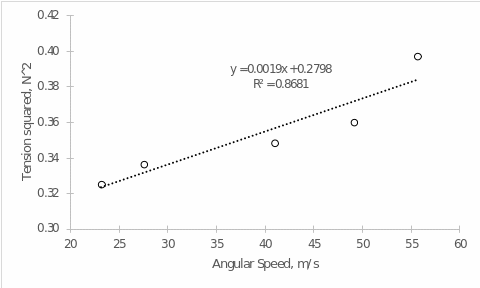
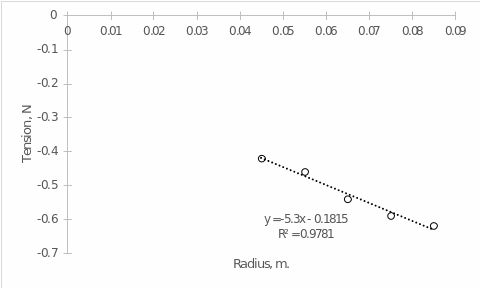
Figure 2 shows the dependence of centripetal force on the radius at which the object was suspended. One can see that the linear trend was downward, which means that when the radius was increased by every one meter, the centripetal force fell by 5.3 N. This fully justifies theoretical expectations, according to which there is an inverse proportionality between centripetal force and radius.
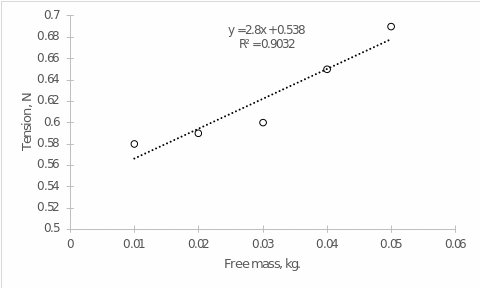
At last, Figure 3 shows the dependence of centripetal force on the free mass of an object. It follows that for each kilogram increase in mass of the object, the centripetal force increases by 2.8 N. Again, this also confirms theoretical expectations because, as the formula shows, there is a direct proportionality between force and mass. Again, it made no physical sense for the y-intercept because there could be no tension at zero mass.
Conclusion
To summarize, this paper investigated the dependences of centripetal force, expressed through the tension of the thread, on the radius, free mass, and angular velocity. The resulting graphs fully confirmed the expected patterns that followed from the formula for the centripetal force. The regression models had high values of the coefficients of determination, which also confirms the reliability of the models. It is also worth noting that any uncertainties may have led to decreased accuracy and errors.
Reference
PHY. (2020). Chapter 6 circular motion [PDF document]. Web.