Computer Vision: Tracking the Hand Using Bayesian Models Research Paper

Introduction

The visual tracking has been a major challenge for the researchers for decades. The visual tracking is a projection of the movement of an object over an extended time frame. Based on the history of the movement, the moving object is checked and projected to identify the future positions it would occupy. This work has brought in a number of theories and working models into fore. The research has existed, particularly, on recognizing hand movement (D Hogg, 1983).

Detection of the movement of hand, recording of the history of such movements, depends on a number of factors. This includes background (V. Athitsos and S. Sclaroff) for the movement, the skin color and even wrist delimitation (R. Rosales, V. Athitsos, L. Sigal, and S. Scarloff) apart from a number of other factors. The speed of the hand movement also plays an important role in identifying or tracking the hand movement (J. M. Rehg and T. Kanade). After the movement has occurred the pose of the hand can be reconstructed using a Kinematic model reconstruction as shown by (Y. Wu and T. S. Huang). In this case also, it can be found that edge conditions, contours and color have to be taken into account when simulating the movement of the hand (V. Athitsos and S. Sclaroff). There had been studies based on both two dimensional (McCormick & Isard) as well as three dimensional movement of hand. In case of two dimensional it is easier because of the limitations in the degrees of freedom. In the case of three dimensional studies, the degrees of freedom are six, whereas it is only four for two dimensions, taking into consideration rigid objects like that of a hand.

In order to bring into focus the entire tracking of the hand, it has been a practice to simulate or build a model of the hand movement. Models are reconstructed based on either planar patches (J. Yang, W. Lu, and A. Waibel), polygon meshes or generalized cylinders. Any of these methods can be employed to bring in a model while simulating the entire track of the hand. In order to mathematically identify the geometric location of the hand, a Bayesian filter is made use of. Many researchers have employed recursive Bayesian filter to realize the model. In many cases, this has been influenced by the Kalman filter and a combination of the two can be employed for the purpose. In the following paragraphs, the Bayesian filter has been adopted for the purpose and is presented below.

Theory of Bayesian Model

Model based studies of the hand movement are based on the following standard processes.

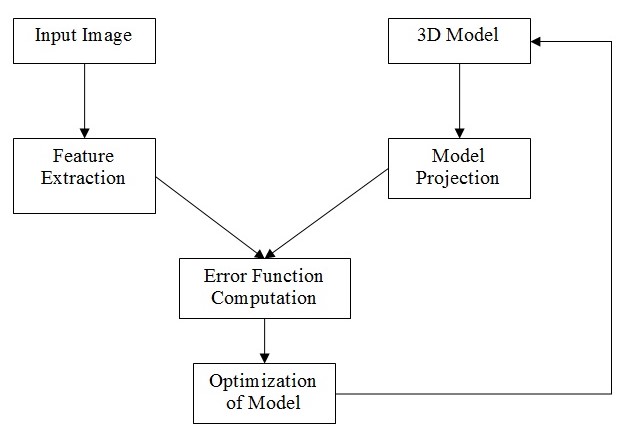
The model collects the input image and does a feature extraction of the inputs. Based on this, it generates a new position and projects the image. A routine is planned that would identify the changes or differences between the actual image and the realized one subsequently. This would, in turn, would bring out the error between the two. The error thus identified is used to bring out a better image using the feedback loop created in the model. This model would provide a closed loop control of the entire work and thereby, enable the model to improve upon itself over a period of time.

Bayesian model is based on the similar structure with a feedback loop in it. Rehg and Kanade, first employed this model for the purpose of building the track of a moving hand. They employed 27 degrees of freedom and reduced the error using the square differences method and reduction using the Gauss-Newton algorithm. The mathematical model below is built based on these concepts.

The Model

Let P_t be the position of the hand at time t in a plane defined by coordinates x and y. In this case let us consider only two dimensional visualizing and a degree of freedom of four.

Therefore, P_t = f(Px_t, Py_t)

Position of the hand at time t-1 will be:

P_t-1 = f(Px_(t-1), Py_(t-1))

The velocity vectors at this point of time t are:

V_t = f(Vx_t, Vy_t)

And at time t-1 it is:

V_t-1 = f(Vx_(t-1), Vy_(t-1))

Based on the probabilistic approach of the recursive Bayesian method, the probability of a specific movement occurring after the current point of time is estimated as Probability Pr. Pr is expected to be any of the degrees of freedom allowed. In this case of two dimensional studies, it is taken to be four or a eight depending upon the need. In this case, we will consider this to be eight. The following probabilities are assumed for this purpose. Pr(left), Pr(right), Pr(up), Pr(down), Pr(left-up), Pr(right-up), Pr(left-down) and Pr(right-down).

As per the first order Markov assumption, the velocity and position at time t is dependent only on the same at t-1.

i.e. V_t = f(V_t-1)

and the second assumption states that the velocity at t will be conditionally independent of all previous velocities. In order to track the movement of a hand, the actual position at time t is taken to be X_t and that of the projected position and velocity at time t as Z_t where X_t and Z_t are the functions of V_t and the error correction or recursive update is a function of both these variables.

The distribution can be taken from the Bayesian rule which indicates for the above variables:

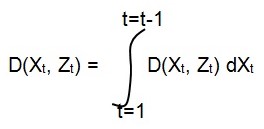
This projection is also called the Chapman-Kolmogorov equation (A. H. Jazwinski).

Conclusion

The ‘slight’ of hand has always been an intriguing prediction problem for the mathematicians and researchers. This probability based prediction bases itself in correcting and learning through the process. This will ensure that the model presented will have the option of becoming better as it progresses and would be able to present a much better result over a period of time. The fitment and the estimation of the probability itself has been varied starting from Gauss Newton algorithm to other normalization distributions.

References

A. H. Jazwinski. Stochastic Processes and Filtering Theory. Academic Press, New York, 1970.

D. Hogg. Model-based vision: a program to see a walking person. Image and Vision Computing, 1(1):5.20, 1983.

V. Athitsos and S. Sclaroff. An appearance-based framework for 3D hand shape classi_cation and camera viewpoint estimation. In IEEE Conference on Face and Gesture Recognition, 45.50, Washington DC, 2002.

R. Rosales, V. Athitsos, L. Sigal, and S. Scarloff. 3D hand pose reconstruction using specialized mappings. In Proc. 8th Int. Conf. on Computer Vision, volume I, 378.385, Vancouver, Canada, 2001.

J. M. Rehg and T. Kanade. Visual tracking of high DOF articulated structures: an application to human hand tracking. In Proc. 3rd European Conf. on Computer Vision, volume II, 35.46, 1994.

J. MacCormick and M. Isard. Partitioned sampling, articulated objects, and interface-quality hand tracking. In Proc. 6th European Conf. on Computer Vision, volume 2, 3.19, Dublin, Ireland, 2000.

Y. Wu and T. S. Huang. Capturing articulated human hand motion: A divide-and conquer approach. In Proc. 7th Int. Conf. on Computer Vision, volume I, 606.611, Corfu, Greece, 1999.

J. Yang, W. Lu, and A. Waibel. Skin-color modeling and adaptation. In Proc. 3^rd Asian Conf. on Computer Vision, 687.694, Hong Kong, China, 1998.