Introduction
Being the most important aspect in microeconomics, production entails the process of product engineering to yield valuable economic outputs (Markovits, 2008). To increase efficiency in production, according to Markovits, a firm has to manipulate a variety of variables and factors of production that include land, labor, and capital. The aim of the research is to determine how a firm can achieve efficiency at a fixed cost of production, which economists refer to as the short run.
The study focuses on an Aerospace engineering company in Singapore specializing in the production of aircraft seat-brackets. With a market share in the range of 30-40 percent, the company is determined to know how a monthly fixed cost would influence the production of brackets. Having performed a research and collected relevant data, exploitation of the production function and other related economic analysis functions are necessary to achieve the company’s goal.
Being in the Aerospace sector, the company in focus is committed in maximizing in profits, therefore this research will assist the firm in economic planning and strategy. The paper employs different microeconomic models to achieve the purpose of analyzing how a fixed cost influences the production of brackets and the corresponding impact on the economy (Cohen, 2000). With an aim of achieving its mandate, the paper employs the Quadratic Average Cost Function with data from regression analysis.
The aim is to analyze results of regression with algebraic parameters, which is possible to achieve with the calculation of output based on the market prices of each bracket. Thereafter, the study gives an economic forecast of the firm and advising appropriately based on the results and analysis of firm production.
Analysis of Results from the Regression Output
The table below is a compilation of the regression output.
According to Cohen, Average Variable Cost (AVC) is a company’s costs of production that change with a variation in output of the firm. The Average Variable Cost Curve is a positive U-shaped curve because in most instances AVC decreases when output rises with a decline in input levels, and then it increases as the output levels rise (Cohen, 2000).
AVC=a+bQ+cQ2 where; a>0, b<0 and c>0
Calculation of the Coefficient of Determination
Usually denoted by R2, the Coefficient of Determination is a vital output in the regression calculation of production. The Coefficient of Correlation being a positive number is the square of correlation between a dependent variable from that of an independent variable. R2 is also the ratio of explainable variation with respect to total variation, meaning it simply highlights how relevant the data is to the relationship among variables (Markovits, 2008). The significance of calculating the Coefficient of Determination is because it establishes the goodness of variables within a production model. With a single independent variable, the formula of calculating the Coefficient of Correlation for a linear regression model is
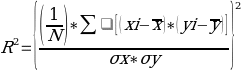
Where;
- N is the total number of observations in the model
- ∑ is the summation of all variables in the equation
- Xi and Yi are observations for x and y respectively
By analyzing the table of regression output above, the R-square value of 0.8343 signifies that 83.43 percent of the Average Variable Cost (AVC) function directly influences the regression output therefore the regression output could explain it. The Coefficient of Determination in this case shows that the 83.43 percent of the data is explainable while 16.57 percent is unexplainable. Subsequently, factors that contribute to the inability of studies to explain data include non-standard collection and data analysis, errors that result from poor data collection instruments, and unqualified data researchers and analysts.
Meanwhile, from the regression table, Cohen shares the view that the high Coefficient of Determination is because of the high correlation between the variables with the scatter diagram fitting the sample regression line. When performing the F-Test, the study shows that the Degree of Freedom for numerator equals two (k-1=2) while the Degree of Freedom for Denominator equals seventeen (n-k=17). At two percent level of significance, critical F is 4.97 and 6.11 at one percent level. However, the computed-ratio of 21.01 is higher than critical F which is 4.97 implying that the regression equation is statistically relevant at two percent level of significance (Cohen, 2000).
The analysis the study performs is the T-Test which shows that at seventeen degrees of freedom with a two percent level of significance, critical T-value becomes 2.567 while the absolute T-ratio values of parameters A and B are 4.7 and 2.6 respectively. Meanwhile parameter C is not statistically significant in regression analysis because its absolute T-ratio value is 1.69 which is lower than the critical T-value. The study reveals that the regression equation as a whole is statistically significant because the P-value for the F-ratio is lower than the acceptable level of significance. In the regression analysis for this output, the P-value for the F-ratio is 0.00027 while the acceptable level of significance is 0.02.
Because the P-value for parameters A and B are 0.0001 and 0.0023 respectively, they are less than the acceptable level of significance of 0.02 therefore both are statistically significant in the analysis. Despite having a P-value of 0.0608 though higher than the acceptable value of 0.02, parameter C is statistically insignificant. With all the data statistically analyzed, the study computes the Average Variable Cost Function.
AVC=50.068-0.01707Q+0.0000022Q2
The Estimated Marginal Cost Function (SMC) =a=2bQ=3cQ2
SMC=50.068-0.03414Q=0.0000066Q2
Meanwhile, the Estimated Total Variable Cost Function
Estimated total variable cost function=a-bQ2+cQ3
Estimated total variable cost function=50.068-0.01707Q2+0.0000022Q3
Assuming that the market price of each bracket is 40 dollars, the study was able to evaluate the marginal cost function (SMC), the number of brackets the firm produces in a month, and the profit resulting from the level of output. Profit maximization is evident at the output level of where the profit equals the Marginal Cost.
P=SMC
40=50.068-0.03414Q+0.0000066Q2
0.0000066Q2-0.03414Q+10.068=0
Apply the quadratic equation of ![]()
Q=-(-0.03414)±√-0.034142-√(4×0.0000066×10.068)÷(2×0.0000066)
Q=4858 brackets
The answer above implies that at a market price of forty dollars, the number of brackets the firm produces is 4858.
Therefore the Average Variable Cost, AVC=a-bQ+cQ2
AVC4858=50.068-0.01707(4858)+0.0000022(48582)
AVC=$ 19.06
After calculating the Average Variable Cost which is 19.06 dollars, the study determined the Total Variable Cost.
TVC4858=AVC×Q
TVC=19.06×4858
TVC=$ 92,604.66
After solving the total variable cost is 92,604.66 dollars, the next important item of production is the total cost of production of the firm’s brackets.
Total Cost=TFC+TVC
TC=80000+92604.66
TC=$172,604.66
With the total cost of production of brackets being 172,604.66 dollars, to calculate the profit of the firm, the study calculates the sum of total revenue and the quantity of brackets the company produces.
Profit=Total Revenue-Total Cost
Total Revenue=P×Q=40×4858
Total Revenue=$194,320
Therefore; profit=TR-TC
=194320-172604.66
P=$21,715.34
The company manages a profit of 21715.34 dollars for 4858 brackets that it produces. To forecast if the price for each bracket will drop to 15 dollars, the study first calculates the output when the Average Variable Cost is at the minimum level.
QMIN= ![]() =-
=-![]() =3879 units
=3879 units
The minimum quantity of brackets the firm can afford to produce is 3879 units.
AVCMIN=50.068-0.01707(3879)+0.0000022(3879)2
AVCMIN=$16.96
When producing 3879 brackets, the Average Variable Cost at its minimum is 16.96 dollars. Because an Average Variable Cost of 15 dollars is lower than the when AVC is at its minimum, the firm should refrain from producing any more brackets. In addition, production of more units beyond the minimum Average Variable Cost is unsustainable because the total revenue the firm earns is unable to cover the total variable costs of production.
If the company produces brackets selling at 15 dollars, it will incur an additional cost on top of the monthly fixed costs there is an additional which might cause a negative impact on its revenue collection. Meanwhile, if the firm decides to stop the production when the price of a single bracket sells at 15 dollars, it will only incur the monthly fixed costs of 80,000 dollars. The study therefore advises the company to consider the recommendation to avoid incurring unnecessary losses.
More Emphasis on Regression Analysis
Being a statistical technique of analyzing relationships between cause and effect of one variable from the next, regression is capable of determining how cost of product influences a company’s revenue. Regression occurs in different forms that include simple regression and multiple regressions. Simple regression type simply analyzes two or more variables while ignoring other factors that are relevant in the study of these variables. For instance, considering the case of this study, regression analysis focuses on only two variables cost of production and profit, while ignoring other factors that are likely to influence production either directly or indirectly. Meanwhile, ‘multiple regressions’ encompasses all factors of production accommodating even less relevant factors.
Benefits of Coefficient of Determination
To determine the extent different dependent and independent variables alternate in regression analysis thereby helping in selection of desired choices of production and profitability. In market where factors vary from time to time, the only easy way to predict the production and market trends is through microeconomic analysis. For instance, this study’s intention was to determine the least number of brackets the firm can produce and still make profits. After analyzing study results, the research advised the company to shut down when prices of brackets reach 15 dollars. Considering firms are normally reluctant to make such decisions without necessary reasons, the research findings eased the work of decision making organs within the company ranks.
Importance of Microeconomic Models
The research study is an important aspect having adopted a unique technique in presenting the importance and implications of economics to both human and firms. To learn the market, understanding the production process is crucial, and trends of various factors are useful in determining a suitable production guideline (Kogiku, 1971). In addition to explaining the non-regulated market economy, the microeconomic models also help people learn how to engage effectively in business because the models increase efficiency. Consequently, it is easier to determine the priority areas that effectively increase revenues of firms.
Firms and businesses alike make decisions that help in profit maximization while reducing the cost of production. To justify why microeconomic models are important aspects in production, firms adopt the policies that aid in both market prediction and decision making. Microeconomic models are not only beneficial to firms but also to individual business people and the governments. When performing daily activities of buying and selling of products, individuals utilize microeconomic principles when deciding on which particular products and services yield maximum utility at lower costs.
Because firms and government institutions have much bigger aspirations and goals than individuals, microeconomic principles affect their well-being more than small businesses, therefore the decisions firms make have a bigger impact on the economy. Decisions the government make emphasize the need of incorporating microeconomic policies in running state institutions and businesses. Significantly, the decisions firms make range from market analysis to ways of reducing the cost of production with an aim of increasing company profits.
Firms and individuals have been employing microeconomic principles within their systems for centuries because the models assist in strategy development and decision making. Equally, companies at times find it hard on choosing the level of products to produce and at what price should each good sell. Because of microeconomic models which eases market prediction and analysis, firms develop the ability to successfully analyze the market trends and decide on the resources to employ with the intended goal of profit maximization guiding the management.
More importantly, because microeconomics believe in a market with no regulations commonly known as a free market, the models predict factors and trends that might affect free flow of markets. Efficiency in service delivery and production is an important aspect in firm development because it enables companies to increase their production levels which results in more revenue gain. To increase a firm’s efficiency, application of microeconomic principles is necessary because of available market prediction indicators which enable firms to capitalize on the market share. Normally, efficiency in production materializes in situations where the price of a product is at par with the minimum Average Total Cost of production. In any case, if such a situation happens, companies resort to a reduction production costs because inability to cope up with the challenge in a pure competition economy might result in massive losses.
Among some of the factors that affect market trends and profitability of companies is taxation. Because the government through its tax systems reaps a lot of revenue from firms in the form of levies and taxes, company management having adopted microeconomic models have the privilege to foresee fiscal actions. With the knowledge of government tax decisions, it is easier for firms to commit necessary planning measures as well as prepare adequately for the changing conditions. To achieve a balance, firms increase production yielding more profits in the process.
Conclusion
Despite the shortcomings that relate to the exclusive employment of microeconomic principles including its partial concentration on certain aspects of the economy and its assumptions of total employment of resources in to the economy, the benefits of microeconomics are many. Firms and small scale businesses should exploit the policies of microeconomic models to strategize on production while increasing profits.
Whether in the short run or long run, a realistic adoption of these principles ensure firms grow financially (Cowell, 1986). Collen emphasizes the need for a clear policy framework within institutions in an attempt to reduce the cost of production so that firms realize increased profitability. Finally, this study has established relevance in successful execution of microeconomic models in a way that enables prediction of market trends and price changes. If adequately employed, microeconomic policies ensure efficient and quality production.
References
Cohen, S. (2000). Microeconomic Policy. New York: Routledge.
Cowell, F. (1986). Microeconomic principles. New York: Oxford University Press.
Kogiku, K. (1971). Microeconomic models. New York: Harper & Row.
Markovits, R. (2008). Truth or economics: On the definition, prediction, and relevance of economic efficiency. New Haven, Conn.: Yale University Press.