Using the similar test rig and identification method, bearing force coefficients are identified in Ref. for an oil-lubricated flexure-pivot tilting-pad bearing at load-between-pad (LBP) and load-on-pad (LOP) configurations. To eliminate the effects from the test rig structures, such as hose connections and pitch stabilizers on bearing force coefficients, the baseline impedances, which are derived from the baseline tests at zero rotor speed without oil supplied, are subtracted from the impedances obtained for each test condition. The experiment data near 60 Hz (electric frequency) and rotor spinning frequency are not included due to the extensive vagueness caused by the electrical noise, shaft run-out, and remnant imbalance excitations. The identified bearing force coefficients correlate well with the predictions both from the classical Reynolds equation modal and a bulk-flow NS equation modal.
San Andrés and Delgado have identified the force coefficients in a squeeze film damper with a mechanical end seal. Two orthogonally positioned electromagnetic shakers deliver independent single frequency load excitations to the bearing housing. The structural support stiffness and system residual damping are estimated from impact tests without the mechanical end seal and lubricants. Further, the dry friction force and corresponding equivalent viscous damping coefficients are evaluated through single frequency excitations with the seal installed but without lubricants. Finally, with the seal mounted and lubricants supplied, the force coefficients of the squeeze film are obtained after subtracting the equivalent force coefficients including structural stiffness, system remnant damping, and dry friction.
With the transferal of load excitations by external excitatory to stators, the excitation forces, frequencies, rotor eccentricities, and bearing response amplitudes can be adjusted easily. Therefore, the frequency-dependent bearing force coefficients at various bearing loads and eccentricities can be obtained. However, this method requires complicated test rig installation and expensive test instrumentations, which limit its extensive application in the industry.
Compared to the identification method with external exciters, the employment of synchronous excitations induced by calibrated imbalance masses for the identification of bearing force coefficients is quite a simple method. If the added mass coefficients are ignored while using low viscosity lubricants, only two independent imbalance tests are required for identifying all the weight-bearing force coefficients—four stiffness coefficients and four damping coefficients. The transfer function relating the bearing forces with the journal synchronous responses gives the bearing force coefficients.
Tawfick et al. presented an identification approach for bearing stiffness and damping coefficients from rotor synchronous responses to imbalances. The bearing housing vibration along with the stiffness and damping coefficients between the bearing housing and foundation are included in the equations of motion. Two linearly independent imbalance responses are quite mandatory to obtain the whole set of bearing dynamic force coefficients. The effects of rotor flexibility on bearing parameters are not considered in the identification model. The identified force coefficients deviate from the predictions markedly. The complete vagueness of the identified cross-coupled stiffness coefficients requires further evaluation.
De Santiago and San Andrés have provided a field identification method for bearing support dynamic force coefficients using rotor synchronous responses to calibrated imbalances. The identification model requires two linearly independent imbalance excitations. The bearing force coefficients are identified from the measured rotor synchronous responses. The cross-coupled stiffness and damping coefficients are ignored in the identification of bearing parameters due to the little cross-coupled effect of the test bearings, tilting-pad type. The identified bearing force coefficients correlate well with the predictions provided in a computational program. Ref. extends this work to incorporate cross-coupled force coefficients and rotor flexibility. Note that the identification approaches in Ref. are restricted to elliptical rotor synchronous motion orbits.
The imbalance-induced excitation method is the simplest in practice since no sophisticated instrument is needed for the excitation. However, most experiments show considerable scatter of identified force coefficient values because the identification equations from imbalance excitations tend to be ill-conditioned. Moreover, the bearing force coefficients (direct and cross-coupled stiffness and damping coefficients) can not be determined when a rotor exhibits circular orbits around bearing centers.
Murphy and Wagner have evaluated the impacts of rotor circular orbits on the identification of bearing force coefficients. Direct force coefficients along with two orthogonal directions are identical (
and
), while cross-coupled force coefficients are identical in magnitudes but with opposite signs (
and 
), which are defined as skew-symmetric bearing force coefficients. This assumption is based on the fact that the lubricant feeding inlet and bearing clearance are both circumferentially uniform, i.e., the bearings are isotropic. The rotor orbits are adjusted as elliptic for identification of all the bearing force coefficients. However, when the rotor motion orbits are circular, direct and cross-coupled force coefficients are combined as equivalent force coefficients for their evaluation. The equivalent stiffness (Ke) and damping (Ce) coefficients are defined as:
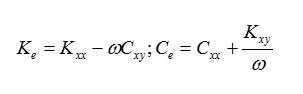
However, Fleming et al. could only obtain the direct bearing force coefficients in the identification from imbalance excitations, because the test bearings were isotropic and the rotor orbits were circular about the bearing center. Moreover, the bearing direct force coefficients are uniform circumferentially for isotropic bearings. The identification equation is:
Only one set of rotor response to calibrated imbalance excitation is required to identify the direct stiffness and damping coefficients.
Zhu and San Andrés present an identification method for bearing direct force coefficients from the measured rotor responses and bearing forces. Since the test gas bearings, flexure pivot tilting pad type, offer little cross-coupling stiffness, the cross-coupled force coefficients are neglected. The direct stiffness and damping coefficients are derived from the simple relationships:
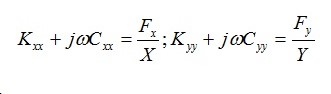
The identified stiffen ss increases with supply pressures, while the damping shows opposite behavior.
Another identification method is based on the rotor transient responses to impacts, which are broad-band excitations in frequency domain. The subtraction of the rotor run-out and remnant imbalance induced rotor synchronous excitations gives the responses solely due to impacts. Bearing force coefficients are extracted from the transfer functions between input impact forces and output rotor transient responses.
Nordmann and Schöllhorn identify the bearing force coefficients using an impact method. Two independent impact forces (along horizontal and vertical directions) and corresponding rotor responses (displacements) are recorded in time domain. The rotor synchronous responses due to residual imbalances are eliminated in time domain. The analytical frequency response functions (FRFs) using linear response model are curve fitted to the measured FRFs via a least square method. The iterative curve fitting procedure gives bearing stiffness and damping coefficients. The good correlation between the calculated (using the identified bearing force coefficients) and measured responses validates the identification approach.
Howard et al. present a simple method for identification of bearing parameters from impact induced responses at various temperatures and bearing loads. The transfer function is derived from the relationship between the vertically positioned impact force and the resulting vertical response. Therefore, only one dimensional direct bearing force coefficients are measured. Even though the identified direct bearing force coefficients are insufficient for comprehensive rotordynamic analysis, still they are capable for indicating the variation of bearing characteristics at different temperatures and loads.
Diaz and San Andrés introduced an identification method from impact tests on a squeeze film damper and an instrumental variable filter (IVF) method, which is an iterative variation of least-square estimation method in a linear system, for extracting all the twelve force coefficients (four added mass coefficients, four stiffness coefficients and four damping coefficients) from transfer functions. Eight impacts exciting conical rotor motions are performed along each orthogonal direction. The impact forces and rotor responses are recorded in time domain. A single frequency response function (FRF) is derived from the average of the eight different FRFs corresponding to each impedance coefficient. The force coefficients are derived from the IVF process, where the weight functions executed through the averaged FRF, can reduce the system noise in the measurements successfully, and consequently, more reliable bearing force coefficients can be identified.
Qiu and Tieu identified all 16 force coefficients of two asymmetric journal bearings from impact responses. Before performing impact tests, the rotor responses to remnant imbalance are recorded. The impact experimental measurement consists of two independent impact forces on the rotor and resulting responses at the two bearing locations. After subtracting the residual imbalance induced responses in frequency domain, the rotor responses solely due to impacts are obtained. Least-square curve fitting of the transfer functions gives whole set of 16 bearing force coefficients.
Using the similar identification procedure, De Santiago and San Andrés determined the bearing force coefficients for a pair of flexure-pivot tilting-pad bearings integrated with squeeze film dampers. The impacts are delivered around the rotor center of gravity along horizontal and vertical directions. With the bearing reaction forces and the responses solely due to impacts, the bearing force coefficients are estimated easily from the transfer function between the input impact forces and output responses. The effects from multiple frequency response averaging on the identified bearing force coefficients are evaluated. Damping coefficients need more impact responses for averaging to obtain converged results than stiffness coefficients.
Some points should be noticed about impact identification methods:
- when bearing force coefficients strongly depend on external excitation frequency rather than rotor spinning frequency, the assumption of independency between the bearing force coefficients and excitation frequency is unreasonable, and thus massive errors will appear in identification;
- when applying the impact method to a spinning shaft, it may lead to irony of input forces due to the friction-related tangential force components.
References
Tiwari, R., Lees, A. W., and Friswell, M. I., 2004, “Identification of Dynamic Bearing Parameters: A Review,” Shock Vibr. Dig., 36, pp. 99-124.
Rouvas, C., and Childs, D. W., 1993, “A Parameter Identification Method for the Rotordynamic Coefficients of a High Reynolds Number Hydrostatic Bearing,” ASME J. Vibr. Acoust., 115, pp. 264-270.
Al-Ghasem, A. M., and Childs, D. W., 2006, “Rotordynamic Coefficients Measurements Versus Predictions for a High-Speed Flexure-Pivot Tilting-Pad Bearing (Load-Between-Pad Configuration),” ASME J. Eng. Gas Power Turbines, 128, pp. 896-906.
Rodriguez, L. E., and Childs, D. W., 2006, “Frequency Dependency of Measured and Predicted Rotordynamic Coefficients for a Load-on-Pad Flexure-Pivot Tilting-Pad Bearing,” ASME J. Tribol., 128, pp. 388-395.
San Andrés, L., 1996, “Turbulent Flow, Flexure-Pivot Hybrid Bearing for Cryogenic Applications,” ASME J. Tribol., 118, pp. 190-200.
San Andrés, L., and Delgado, A., 2007, “Identification of Force Coefficients in a Squeeze Film Damper with a Mechanical End Seal – Centered Circular Orbit Tests,” ASME J. of Tribol., 129, pp. 660-668.
Tawfick, S. H., and El-Shafei, A., 2008, “Field Identification of Stiffness and Damping Characteristics of Fluid Film Bearings,” ASME Proc. GT2008-50909.
De Santiago, O. C., and San Andrés, L., 2007, “Field Methods for Identification of Bearing Support Parameters— Part II: Identification from Rotor Dynamic Response due to Imbalances,” ASME J. Eng. Gas Turbines Power, 129, pp. 213-219.
De Santiago, O., and San Andres, L., 2006, “Experimental Identification of Bearing Dynamic Force Coefficients in A Flexible Rotor—Further Developments,” STLE Tribol. Trans., 50, pp. 114-126.
Goodwin, M. J., 1991, “Experimental Techniques for Bearing Impedance Measurement,” ASME J. Eng. Ind., 113, pp. 335-342.
Murphy, B. T., and Wagner, M. N., 1991, “Measurement of Rotordynamic Coefficients for a Hydrostatic Radial Bearing,” ASME J. Tribol., 113, pp. 518-525.
Fleming, D. P., Thayer, W. J., and Cunningham, R. E., 1977, “Dynamic Stiffness and Damping of Externally Pressurized Gas Lubricated Journal Bearings,” ASME J. Lubr. Tech., 99, pp. 101-105.
Zhu, X., and San Andrés, L., 2007, “Rotordynamic Performance of Flexure Pivot Hydrostatic Gas Bearings for Oil-Free Turbomachinery,” ASME J. Eng. Gas Turbines Power, 129, pp. 1020-1027.
Nordmann, R., and Schöllhorn, K., 1980, “Identification of Stiffness and Damping Coefficients of Journal Bearings by Means of the Impact Method,” Proceedings ofthe 2ndInternational Conference on Vibration in Rotating Machinery, IMechE, Cambridge, UK, Paper C285, pp. 231-238.
Howard, S. A., Dellacorte C., Valco, M. J., Prahl, J. M., and Heshmat, H., 2001, “Dynamic Stiffness and Damping Characteristics of a High-Temperature Air Foil Journal Bearing,” Tribol. Trans., 44, pp. 657-663.
Diaz, S., and San Andres, L., 1999, “A Method for Identification of Bearing Force Coefficients and Its Application to a Squeeze Film Damper with a Bubbly Lubricant,” STLE Tribol. Trans., 42, pp. 739-746.
Qiu, Z. L., and Tieu, A. K., 1997, “Identification of Sixteen Force Coefficients of Two Journal Bearings from Impulse Responses,” Wear, 212, pp. 206-212.
De Santiago, O. C., and San Andrés, L., 2007, “Field Methods for Identification of Bearing Support Parameters— Part I: Identification from Transient Rotor Dynamic Response due to Impacts,” ASME J. Eng. Gas Turbines Power, 129, pp. 205-212.