Introduction
Factor analysis is a useful exploratory tool which is helpful in determining the number of factors that should be extracted. The factors that are extracted are those that have a meaningful share of variance and the rest of the variables and their interrelationships are discarded.
Variables which exhibit maximal correlation are clustered together while variables with equivalent minimal correlations are also grouped together. In the end, it becomes possible to establish a relationship(s) or factors which display the data candidly leaving out the less significant factors out.
An interpretation of the factor loadings is essential in correlating extracted factors with meaningful variables (Newcastle University, 2007). For this project, the aim is to find out commonalities that are likely to exist between four variables i.e. rath (Rathus assertiveness Scale), crwone-marlowe (Crowne-Marlowe Social Desirability Scale), axin (“Anger in” scale) and axout (“Anger out” scale).
Complete_mooney_bp.sav dataset based on the four variables was used to conduct Factor analysis. It is speculated that up to three factors are measured by the four instruments (scales).
Descriptive statistics and correlations
All the factors have the same sample size, N = 63. The mean for crowne-marlowe is.6829 and a standard deviation of.0762. Axin had a mean of 2.2560 with a standard deviation of.4543 while axout had a mean of 2.1071 with a standard deviation of.4277. Finally, the mean for rath was 3.3860 with a standard deviation of.4370.
From the means, it is evident that rath i.e. assertiveness is the most important factor in determining anger in, anger out or even social desirability as it has the highest mean of 3.3860, followed by axin, axout and crowne-marlowe social desirability is the least influential variable.
In summary, the Rathus assertiveness scale has the highest likelihood of being among the factors that should be retained. The “Anger Out” scale, the “Anger Out” scale and the Crowne-marlowe desirability scales then follow in that order.
The Pearson correlation coefficients and their single-tailed significance values are presented in Table 2. There is a weak negative Pearson correlation between axin and crowne-marlowe and this is statistically significant, r = -.247, p =.026. A negative and weak Pearson correlation also exists between axout and crowne-marlowe but this is not statistically significant, r = -.197, p =.060.
Rath and crowne-marlowe have a very weak positive correlation which is not statistically significant, r =.048, p =.353.
There is a weak negative correlation between axout and axin which is not statistically significant, r = -.005, p =.486 whereas the correlation between rath and axin is negative but statistically significant, r = -.383, p=.001. There exists a weak positive correlation between rath and axout and the correlation is statistically significant, r =.286, p =.012. All correlations between variables and themselves are 1.
Communalities
Table 3 indicates the communalities prior to and after extraction. The extraction method utilized in this case is the principal component analysis whose assumption is that there is commonness in all variance. That is the reason why the communalities for all factors are 1 prior to extraction. The ‘’extraction” column provides the common variance exhibited in the data structure.
It is therefore correct to say that 65.6 percent of variance associated with crowne-marlowe is common/shared variance or.656 of variance is explained by crowne-marlowe. A communality of.697 for axin after extraction indicates that 69.7 percent of variance associated with axin is shared variance, which can also be stated that.697 is the amount of variance in axin that is explained by the two retained factors (factor 1 and factor 2).
A communality of.703 for axout after extraction implies that 70.3 percent of variance associated with axout is shared variance or.703 is the amount of variance in axout that is explained by factor 1 and factor 2 as the retained factors. Finally, a communality of.733 for rath is an indication that 73.3 percent of variance associated with rath is common variance or.733 is the amount of variance in rath that is explained factor 1 and factor 2.
Consideration for whether to use the Kaiser criterion (where factors with eigenvalues above 1 are retained) or the Scree Plot in determining the factors that should be retained is made depending on the sample size, number of variables and average communality.
Field (2005) explains that the Kaiser’s criterion is used if average communality is at least 0.7 and the variables are not more than 30. In addition, the same criterion is considered if the sample size is more than 250 with an average communality of at least 0.6.
Failure to meet any of the above conditions calls for the use of the Scree Plot bur the sample size has to be large enough i.e. at least a sample size of 300. In this project, the average communality was 2.789/4 =.69725, there were 4 variables and the sample size was less than 250.
As such, the Kaiser’s criterion was applied since the communality is approximately 0.7 and the variables are less than 30 and hence the first condition was met. This led to the retention of all factors with an Eigen value above 1 (Factor 1 and Factor 2.
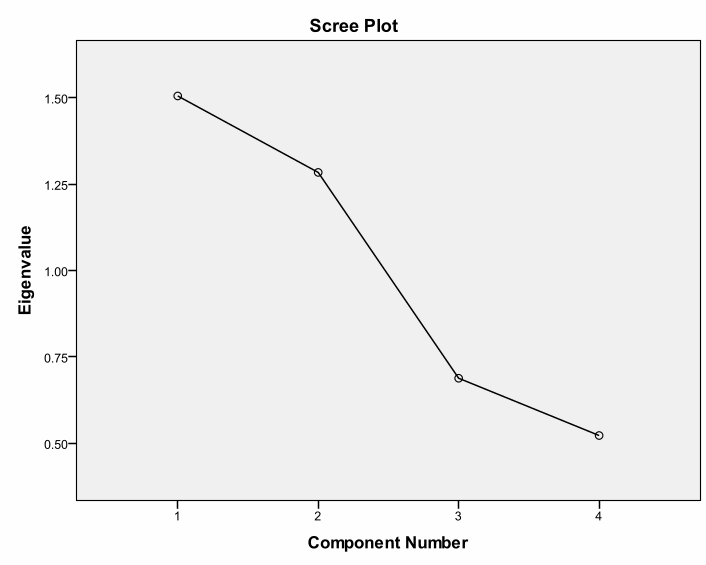
Even going with the Scree Plot (Figure 1) which is suitable for sample sizes that are larger than 300, the first point of inflexion is after the second factor and it is clear that the Eigenvalue is greater than 1. It is therefore justifiable to retain two factors only i.e. the first and the second factor, since they lie above eigenvalue 1 and appear before the graph starts to flatten.
Variance explained
The Eigenvalues associated with every factor (linear component) prior to extraction and after extraction are provided in Table 4. Prior to extraction, it is evident that there were 4 linear components in the complete_mooney_bp.sav dataset. The variance explained by every factor is given by correspondent Eigenvalues and these are displayed in percentage form.
In that case, factor 1 explains 37.636 percent variance whereas factor 2 explains 32.102 percent variance. Only two factors have Eigen values greater than 1 in this dataset and therefore only the two factors are extracted (factor 1 and factor 2) and the other two factors can be considered as non-significant.
The Eigenvalues and percentage variance for the two extracted factors are again displayed under the ‘Extraction Sums of Squared Loadings’ column.
It is evident that the cumulative variance that is explained by both factor 1 and factor 2 (extracted factors) is 69.738 percent variance. From the ‘total variance explained’ output, it becomes clear that the largest variance is given by factor 1 and factor 2 and discarding the rest of the factors is justifiable.
Component matrix
Table 5 is a component matrix table prior to rotation and the loading of each variable onto the two extracted factors is provided. In this case, all loadings were produced where the loading of crwone-marlowe onto extracted factor 1 is.327 and -.741 onto factor 2.
Axin has a loading of -.782 on factor 1 and a loading of.290 onto factor 2. The loading of axout onto factor 1 was.343 whereas the loading of axout for factor 2 is.766. Finally, the loading of rath onto factor 1 is.818 with the loading of rath onto factor 2 being.253.
It is also possible to view Table 5 as correlations between variables and the various unrotated factors. In that case, the correlation between crowne-marlowe and factor 1 is.327 whereas the correlation between crowne-marlowe and factor 2 is -.741.
The correlation between axin and factor 1 is -.782 while the correlation between the same variable and factor 2 is.290. The correlation between axout and factor 1 and factor 2 is.343 and.766 respectively. Finally, the correlation between rath and factor 1 is.818 and the correlation between rath and factor 2 is.253.
It is evident that rath has and axin has the highest loading/strongest correlation with factor 1 while crowne-marlowe and axout have the highest loading on factor 2. Since the highest load on factor 1 is rath, it is arguable to label factor 1 as assertiveness (based on Rathus Assertiveness Scale).
On the other hand, axout seems to have the highest loading on factor 2 and thus it is arguable that factor 2 can be labeled as tendency to let anger out. From the interpretations of the component matrix it appears that the researcher was mainly/or should concentrate on finding out the relationship between assertiveness and tendency to express anger out.
In other words, it is evident that at least two factors are measured by both the Rathus Assertiveness Scale and the “Anger Out” scale. Indeed, it can be said that the more an individual is assertive, the less likely the individual is to hold anger “in.” In other words, assertive individuals tend to express anger more openly. Increased assertiveness leads to decreased tendency to hold anger in.
Summary
Factor analysis is helpful in determining which variables should be retained by looking for variables with maximal relationships. From the above factor analysis, it has been demonstrated that among the four variables i.e. Rathus Assertiveness Scale, Crowne-Marlowe Desirability Scale, “Anger Out” scale and “Anger In” scale, there exists stronger correlations between factor 1 and Rathus Assertiveness Scale and factor 2 with “Anger Out” scale.
This is demonstrated by high means for these variables and the fact that they are the only factors that are extracted, or meeting criteria for extraction in the analysis. The variances explained by the two factors have a lion share in the total variance with a cumulative variance of 69.738 percent being registered for factor 1 and factor 2.
The variance that is explained by factor 1 alone is large enough (37.636%) to qualify the factor for retention. This is the same with factor 2 which explains 32.102% of the variance.
Moreover, both factor 1 and factor 2 have eigenvalues above 1. Finally, the loadings of the two factors on the variables are of significance with factor 1 having a loading of.818 onto rath (Rathus Assertivness Scale) while factor 2 had a loading of.766 onto factor 2.
It is from these observations that it is concluded that factor 1 can be labeled as the Rathus Assertiveness Scale while factor 2 is labeled as “Anger Out” scale. These two variables are therefore essentially important in the study and for sure, assertiveness and tendency to express “anger out” can be measured by these two instruments (scales).
Appendix
Table 1: Descriptive Statistics.
Table 2: Correlations of all Factors.
Table 3: Communalities-Before and after Extraction.
Table 4: Total Variances (Variance and Cumulative Variance).
Table 5: Component Matrix.
Reference
Field, A. P. (2005). Discovering statistics using SPSS (2nd edition). Sage: London.
Newcastle University. (2007). How to perform and interpret Factor Analysis using SPSS. Web.