For centuries, mathematicians, designers, architects, and artists have explored the use of the golden mean ratio in different areas of designs and nature. These professionals have found the application of the golden mean ratio in designs to enhance beauty. The golden mean ratio is a naturally occurring concept. One may wonder what the magic ratio is. In principle, the golden mean ratio is 1.6188. However, for artistic purposes, the ratio is normally reduced to 1:1.5 or 2:3. This figure is so significant that many Renaissance artists and writers had focused on it or mentioned it in their works. The Greek Phi denotes the golden ratio, golden mean, or divine proportion among other names given to it. Euclid wrote about the golden ratio in 300 B.C while the most recent work about the ratio was in Dan Brown’s novel, The Da Vinci Code.
From a mathematical perspective, two measures can achieve the golden mean ratio when the longer section divided by the shorter section is equal to the entire length divided by the longer section.
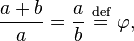
(φ) = the Greek phi which indicates the golden ratio
The standard value of the golden mean ratio is:
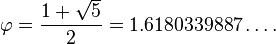
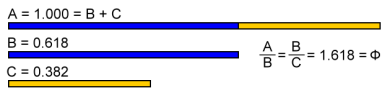
Few curricula talk about Phi in schools. In order to understand the concept and expressions of Phi, one must go beyond the academic sphere and embrace the spiritual aspects as well. In this respect, the golden ratio shows unique design that captures several aspects of life. However, the Greek Phi remains an irrational concept, which has several, infinite numbers after the decimal place. While one can cut a string at any place and obtain a ratio of the whole, there is a unique position, which if cut, provides the golden ratio at 1.618 to 1.
The concept of the golden ratio has achieved uniqueness and becomes a fascinating exercise in mathematics because the ratio appears in several elements and creations, such as the human body and face. Moreover, analyses of other animals, plants, and the solar system have also revealed the golden ratio. At the same time, others have noted the pattern of the ratio in the price and instances of the stock markets and trading in foreign currency exchange. Thus, the golden ratio cuts across various fields from natural, artistic, mathematics to investments.
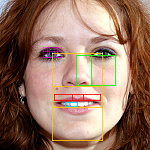
The Greek Phi is also in geometry. One may find the golden ratio in basic elements like equilateral triangle, pentagon, and square when placed within a circle (Avramović, Vladić, Kašiković and Ivan 30). Still, these figures in three-dimensional blocks would reveal the golden ratio. These elements of geometry depict mathematical relationships and uniqueness of Phi. One can only explore Phi in depth in order to understand it. For now, one can observe nature and denote fascinating manifestations of the golden ratio in flowers and animals. The positions and sections of key measures of many animals rely on the golden ratio. A closer analysis of the body parts and wings of an insect would reveal these unique patterns. The spiral lines on the seashell and the location of the dorsal fins reveals the concept of the golden ratio. The most fascinating discovery is the presence of Phi on most sections of the human body, such as face, fingers, body, and even the teeth. These proportions affect how one perceives human beauty and aesthetic in other works of art.
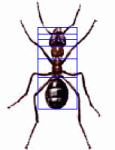
Although people may argue that beauty is relative, there are credible discoveries and evidence in scientific investigations to support the concept of human beauty and its relationships to proportions of the body and face, which relates to the golden ratio. As a result, the concept of Phi is critical in explaining human beauty. For this reason, surgeons have applied the golden ratio in both cosmetic and facial plastic surgeries. This allows such professionals to perfect and achieve the natural beauty, qualities, and manifestation in designs.

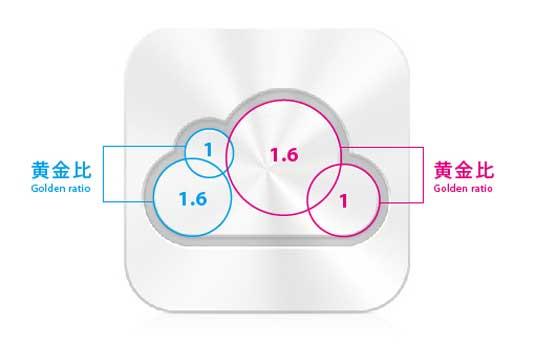
Given the unique mathematical attributes of the golden ratio and its presence in most creatures, man took interest in it. As a result, several works of art, architecture, fashion designs, Web designs, logos, and other areas of designs have applied the concept of the golden ratio to capture the ultimate beauty. Therefore, artistic use of Phi is undeniable. Today, Phi may generate debate as engineers strive to capture it in technologies and modern software. The Apple’s iCloud icon captures the modern use of the golden ratio in designing company logos.
In buildings and construction, the Egyptian Pyramid depicts the golden ratio in its base, hypotenuse, and height. However, the Pyramid’s current state of depreciation and the failure to capture Phi aspects in writing present obstacles to proving the use of Phi in the design. It is undeniable that the golden ratio has found its way in many areas in which it is hard to believe that designers could have applied it in their works. The most valuable Stradivarius violin of 1700 also shows the application of Phi. This is one area many believed that the use of the golden ratio would never be present. At the same time, modern applications of the golden ratio have also emerged in different designs and construction. For instance, designers of the United Nations building situated in New York and Notre Dame of Paris applied the golden ratio in their works. Today, major organizations rely on the concept to create beautiful, iconic logos.
The most important part of this essay is the use of the golden ratio in fashion clothing designs. There are ‘Phi Collection’ designers who apply the golden ratio and Fibonacci concepts to design their clothes. These fashion designers include Elle, Vogue, and Vanity Fair.

They believe that the golden ratio has a natural appeal of beauty to people (Stecker 75). In this regard, the beauty of the golden ratio attracts people irrespective of their cultures or even if they are not aware of its mathematical relations.
One may wonder what the golden ratio, 1.618 has to do with tailors and sewing clothes. Fashion designers have established that the use of the golden ratio results in attractive and harmonious parts of the garment, more so with consideration of lengths of different parts of the human body.
When fashion designers apply the golden ratio, they can decide on how to make the best clothes that fit the body. In this case, they consider lengths of jackets against trousers, the length, and width of the collar among other parts of the cloth. For instance, a fashion designer who applies the golden ratio rule in this case would get harmonious outfit.
The length of the jacket = 66 cm
What is the length skirt or trouser required to be visible?
A =?
B = 66
A/B = 1.618
A/66*1.618 =
B = 106.7 cm
106.7/66 = 1.6
Hence, the required length of the skirt would be 106 cm.

A clear example of the use of the golden ratio is in the works of Sara and Ruth Lee (Mannes 1-2). The sisters apply the concept of the golden ratio to find the perfect fit for their clients. They noted that past designers and artists had applied the golden ratio in their works in order to achieve a perfect visual balance. They reviewed the works of da Vinci and the portrait of Mona Lisa and noted the concept. These fashion designers have applied the golden ratio concept in their Rancho Santa Fe fashion business. They refer to the ratio as the fashion code. Ruth and Sara use the ratio to determine measurements required for outfits’ hemlines and other parts of the cloth. Customers can change their garments based on the golden ratio in order to look attractive and flattering. A mathematical calculation would show exactly what length of a neckline is required for a given client and the garment.


Still, fashion designers have applied the rule of the thirds (1/2 or 2/3) in order to make designs. They derived it from 1.6 by reducing their measurements. In the rule of thirds, designers break up a picture into three parts and determine both vertical and horizontal lines and their intersections. Intersection points are important for placing a given visual constituent. The rule of the thirds has guided many fashion designers to determine the correct designs.


Some critics of fashion designers have claimed that the application of the golden ratio in clothing design has become extreme. They claim that too much mathematics and science in artworks may distort beauty. In some cases, the beauty may be imperfect. Perfect tailoring and unity of lengths alongside chaotic patterns could create the attractiveness required. Good designers should apply both harmony balanced with the golden ratio. In addition, the fashion must also account for contents. In other words, fashion should not be timeless and short-lived in terms of message.
The golden ratio or the rule of the thirds also guides fashion designers to match the best colors. The aim of matching colors is to avoid uneven parts and patterns when one dresses. For instance, the ratio of 1:1 would look blocky, unattractive, and boxy. However, the ratio of 1:2 would result into elongated, flattering figure. In this case, the rule of the thirds (1/3 or 2/3) applies.
A good designer and mathematician should be able to identify the divine proportion of Phi in designs. It explains most concepts found in designs. Understanding proportions is a critical rule in designing. It is the perfect approach for laying out and understanding required lengths of garments. However, designers must recognize that Phi is not the only tool in design. Hence, they must consider other guidelines and elements involved in design. Visual elements should enhance composition alongside texture, colors, balance, and shape of the body among other features.
Works Cited
Avramović, Darko, Gojko Vladić, Nemanja Kašiković and Pinćjer Ivan. “Applicability of golden ratio rule in modern product design.” Journal of Graphic Engineering and Design 4.1 (2013): 28-35. Print.
Mannes, Tanya. Golden ratio lends itself to fashion. 2010. Web.
Stecker, Pamela. The Fashion Design Manual. South Yarra: Macmillan Education, 2006. Print.