Introduction
Fault Tree Analysis and Event Tree Analysis are hazard assessment tools that have been widely used estimate the likelihood of occurrence of accidents and other undesired losses in life’s events. They help identify and detect hazards in a system or facility and give a provisional evaluation of any scenario that may lead to events that can be considered potentially hazardous (Acharya et al. 1990).
With increased sharing of information and the use of internet and computerization created a challenge that had to be handled: the challenge of security of these security models and intelligence that was to be shared. This then made the importance of the safety aspect in any industry become one of the main sources of its success.
In search of security models and systems such tools like fault tree, event tree, failure mode effect analysis, and reliability block diagram emerged as a way to assess system’s safety. This paper is a detailed study of the concept of Fault Tree analysis and Event Tree Analysis with a focus on the safety injection system (SIS).
Fault tree analysis refers to a graphical representation of an interaction of failures which lead to a defined top event. A Fault Tree Analysis (FTA) is developed using a “top-down” approach, and is a powerful tool for modeling combinations of independent and common mode failures.
They are used to capture both hardware and human errors. Event tree analysis, on the other hand, is a graphical representation of logic, showing how the time sequences of events develop. They can be multiple outcomes, and are mostly used with binary branches (Rechard 1999).
In the fault tree analysis, minimum cut sets are crucial in pointing out leads to undesired events that may result to top-event. In the event tree analysis, the steps to be followed are: identifying the initiating event; identifying safeguards and then determining the outcomes; constructing event tree on the basis of all customers; classifying the outcomes in groups with consequences that are similar; quantifying branch probabilities; quantifying outcomes; and testing outcomes.
Thus, an event tree is simply a graphical illustration of scenarios of events that are likely to result from an initiating-event.
Definition of the Problem
The problem for which this system is designed is the problem of losing of coolant from a nuclear reactant plant. It is crucial to have a well operational system for a nuclear plant given the danger that the plant poses to the environment and the lives of those working on it and residing in its vicinity.
It therefore crucial for every part of it to operate fully well and satisfactory which means that failures of such a crucial place as the coolant is of great importance to the proper running of the system and its safety to those working on it (Gianni 2006).
Description of the System together with its Schematic and Principle of Operations
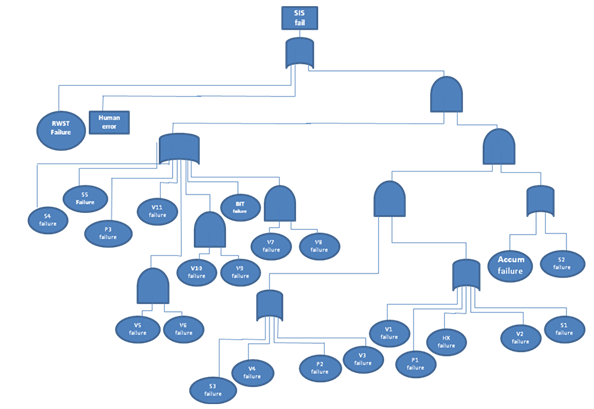
The illustration in figure 1 shows the safety injection pump flow paths. The major components of the system include the accumulators, the storage tanks, the pressure pumps, and the containment sump. The safety injection pump functions in two phases, the first being the injection or the suction from the tank into the reactor, and the recirculation phase wherein the pumps suck from the containment sump.
They key objectives of a nuclear safety system includes shutting down the reactor, ensuring it remains shut down and preventing any discharge of radioactive materials in case of accidents or unfortunate events. A safety injection system makes use of the variations of the density of water in inducing natural circulatory flow (Hixenbaugh 1968).
For nuclear power plants, a kind of emergency water system is important in cases where normal functioning may be lost or in cases where there may be an occurrence of a major breakdown. The safety injection pump system is a very important component in any given system especially in a nuclear power plant where a lot of heat is generated.
The failure of a safety injection system thus has fatal implications to the system and an elaborate risk assessment is essential to contain the situation. The heat exchanger is also a vital part of the nuclear power reactor which is responsible for the cooling and therefore its failure is tremendous to the operation of the system.

Data Sources and Assumptions for Reliability and Human Error Data
Calculation of Failure Probability
In the calculation of the failure probability of the system, the test intervals that have been taken were done so at the interval of three months each.
This information is shown in the table 1 below. This failure rate data was taken from books which contained quantitative risk assessment methods and the past research which have been conducted to determine probabilities of failures of the various components or the events in a given system identical to the one under study.
Computation
The computational formula was FP= FRD x time in hours/2
Given a test interval of three months, the time interval was taken to be 2190 hours, obtained as (365 days x 24 hours) x (3 /12 months) = 2190 hours
For example, the failure probability (FP) for the RWST = 63E-6*2190/2 = 3.942E-3
Where 22.456E-6 is the failure rate data for the core obtained from the available literature (Gertman and Blackman 1994). The rest of the computations are summarised below
Analysis Results and Conclusions
The second column of the Table shows a brief description of the failure; column three shows the failure rate data obtained from available literature (Gertman & Blackman 1994); the fourth column shows the assumed reference of the failure rate, while the last column displays the failure probability.
Fault tree analysis logically explains how and why a failure might come about (Aven 2008). An appropriate design of a Fault Tree Analysis has to have specific elements that have to be done key of which are:
- The gate symbols and types should be set so as to represent fault tree logic
- A top-down approach ought to be employed
- Failure modes ought to be identified.

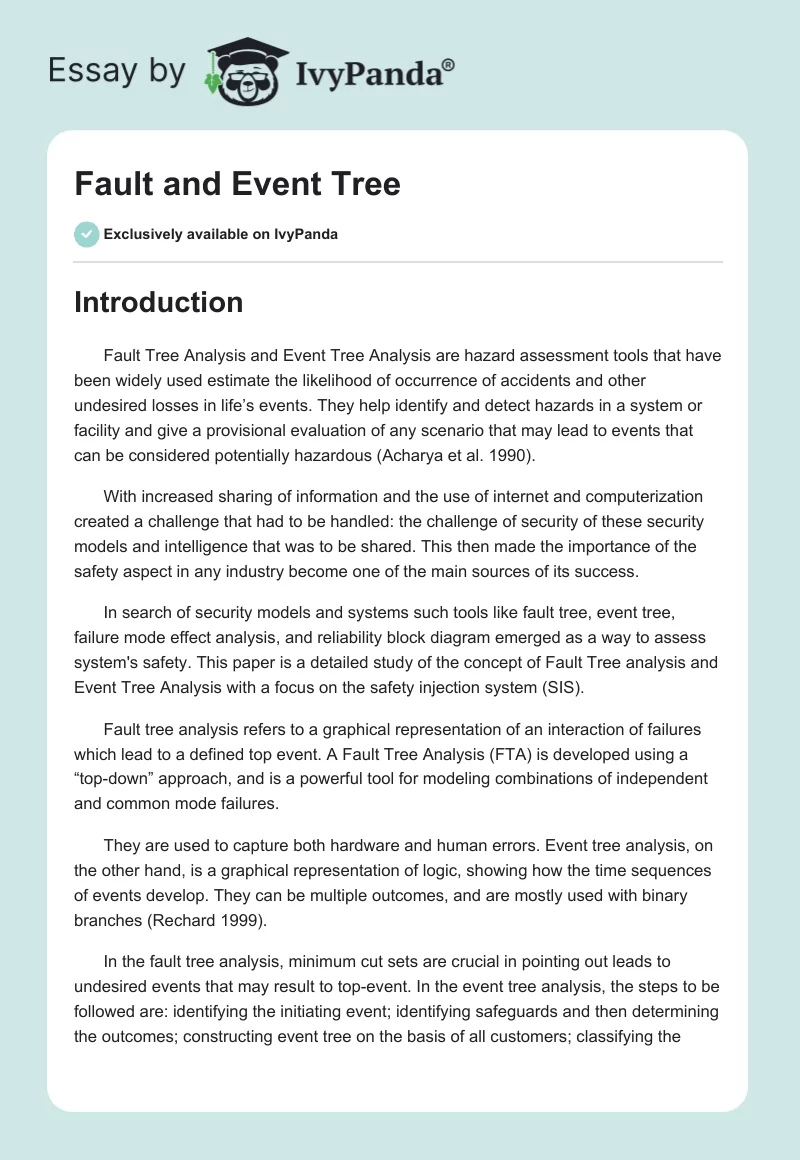
The minimum cut set table makes use of AND gates in computation of the probabilities. This means that all the components in Table 2 are AND gates and are therefore multiplied. Cut set values are obtained by multiplying probabilities of two related components in the system. These cut set values are very vital in fault tree analysis since they show trends for different fault points in a given system.
Minimum cut sets for a simple fault tree such as this for an injection system could be directly determined “from the fault tree or from the associated reliability diagram” (Aven 2008, p. 75).
However for more complex fault tree diagrams, computer programs can be written to compute it automatically. The probabilities of individual components in the system were obtained from Table 1. In this system, the following formula was applied (for the first cut set):
(Probability of RWST) X( High Pressure Safety Injection Pump(HPSIP)) = the probability of time RWST with High Pressure Safety Injection Pump.
For example, RWSTX High Pressure Safety Injection (HPSI) Pump (HPSIP) = 3.942 E-3*1.606 E-4= 1.683e-7. Cut set values for the whole system are found in this manner.
The total probability of failure to cool the RSWT on demand was found to be 2.858 E-5. This number will be the Total Probability TP.
Fussel Vessely and Birnbaum
Fussel vessely and birnbaum values play a critical role in fault tree analysis. These values also indicate probability of a risk in the system. The Fussel Vessely is obtained by adding all the probabilities containing a specific component in table 2 then dividing by the total probability TP found in table 2 (Ericson 1999).
An example can be given as
(Core.SIS) + (Core. SP)/TP= (1.676+1.536)E-5/4.673E-5=0.676
Birnbaum values are obtained by taking the sum of probability in table 2 and dividing by the specific component probability (Gianni 2006).
For example, Core/TP= 22.44E-5/4.673E-5=0.481 (Lindsay 1997).
It is obvious that more emphasis should be given to the core in the AC power supply parts to increase the reliability of the safety injection system. Both Fussel Vessely and Birnbaum analyses concurred on this matter. The major contributor to the failure probability is common mode failure in the AC power supply parts of the safety injection system.
Also, it is much easier and cheaper to increase the reliability of the DC system than the AC part. For instance, the Fussel Vessely analysis indicates that increasing the reliability of switches can increase reliability significantly.
So, it is easy to do so by using diversification, redundancy, segregation of switches to increase the reliability of the DC system. Meanwhile, Birnbaum analysis indicates that more diversified batteries will achieve higher reliability. This also can be easily achieved.
The fault tree diagram is ascertained by using both the table of failure rate and failure probabilities and the minimum cut sets. This is done based on the assessment of the results and in this case the top event is RWST. However, realistic failure of this event will emanate from sequential failure events that fall under the top event. The probability value is used in the development of a fault tree.
The failure of a given part in the event tree is ascertained by using a AND logic function for all the components which make up that particular part. The various parts’ probabilities of failure are then combined using OR gate so that they can built up to the ultimate event which is a representation of the all system (Fayssal 2000).
Moreover the cut set values are the most probable causes of the failure of the top event. The main reason for the use of cut set values is that they are critical in the analysis of the fault tree since they give the various combinations which lead to failure junctions in the all system. In this case the cooling system displays multiple fault points indicated by either AND or OR gate depending on the relationship of the preceding events or components.
Event Tree Analysis Model for Plant Hazard
To illustrate the event tree analysis, several hypothetical scenarios were analyzed. First is the scenario where a valve fails to open or close as required, taking for instance v2, then the heat exchange will not get the heated water from the reactor and therefore there will be no heat exchange taking place.
The pump p1 will fail to function and as a result the valve v1 will also not function and thus the top event which is the RWST will be affected.
A second scenario is where the heat exchange fails to function as expected and therefore the heat from the reactor is not removed. This means that the heat is returned back to the reaction chambers therefore this makes the reactor to malfunction or melt.
RWST will be affected since the hot fluid in the reaction chamber which is meant to be cooled first before circulating back remains hot. The heat exchanger is also meant to transfer heat to be reused in the system but when this fails it means that heat is wasted.
The cooling system with no doubt will fail whenever any of the activities which lead to the top most event, RWST malfunctions. It is evident therefore that the failure of one of the events in the event tree will lead to malfunctioning of the preceding event in t and eventually affect the top most event in the system.
This calls for effective measure to be put in place to mitigate the failure of any of the events in the event tree. The event tree analysis in this case was conducted in a qualitative manner (Faysbe et al 2000).
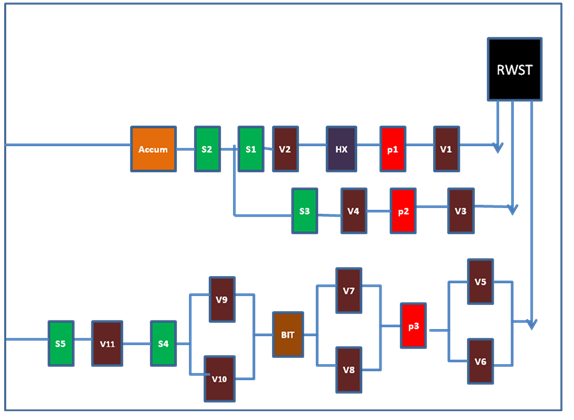
This analysis is based on the event of core failure as discussed hereunder. The core can melt the moment a relentless, compounded failure of a system or components makes the reactor-core to stop being cooled properly, thus making its assemblies to be overheated and/or melt and hence may cause them to explode. Typically, the event tree analysis is created with the aim of illustrating the various impacts of the core event.
Event Tree Analysis Assessment, results and Conclusion
Given the results obtained and indicated above, there are several conclusions that can be drawn from the foregoing discussion for the Event Tree Analysis. It can be seen that the impact with the highest probability is valve failure and/ or heat exchange failure, which haves a probability of as high as 50 percent.
The explanation for this is that the valve is likely to have failed and therefore remained open. In actual sense, heat exchange failure can lead to a core melt making the reactor unusable until the power plant is repaired. The corollary of this is that the operator will incur additional expenses, or effort to prevent this from taking place or to repair it (Eckberg 1964).
Conclusion
The main objective behind all hazard assessment tools such fault tree analysis (FTA) and event tree analysis (ETA) is to identify hazards in a facility, and evaluate any possible scenario that leads to unwanted events. Identifying the hazards is a crucial step in risk management. If hazards were not identified, they will not be managed (Launer 2005).
All in all, Fault Tree and Event Tree Analysis are among the most proficient methods of risk assessment and this takes special specialty when they are used to identify the most probable causes of failure in a system as well as giving particular details of cases of multiple failures.
The tree analyses are important especially in the nuclear industry because of the involvement of huge costs and substantial effort. In the fault tree analysis, minimum cut sets are crucial in pointing out leads to undesired events that may result to top-event.
The foregoing discussions, assessments, designs and conclusions of the application of ETA and FTA to a nuclear power plant specifically referring to the problem of failure in the plant’s safety injection system greatly helps to pontificate this idea of the centrality of these methods in fault determination and failure identification in systems.
They key objectives of a nuclear safety system includes shutting down the reactor, ensuring it remains shut down and preventing any discharge of radioactive materials in case of accidents or unfortunate events.
The effectiveness of these methods therefore makes them centrally important in the formulation of possible remedies to foreseen failures in different systems and plants in any industrial design as well as corporations.
References
Acharya et al., 1990. Severe Accident Risks: An Assessment for Five U.S. Nuclear Power Plants. Washington, DC: U.S. Nuclear Regulatory Commission.
Aven, T., 2008. Risk Analysis: Assessing Uncertainties Beyond Expected Values and Probabilities. Wiley: Chichester.
Eckberg, C.R., 1964. Fault Tree Analysis Program Plan. Seattle, WA: The Boeing Company.
Ericson, C., 1999. Fault Tree Analysis – A History, Proceedings of the 17th International Systems Safety Conference. Washington: Seattle.
Fayssal, S., 2000. Overview of Quantitative Risk Assessment Methods. MSFC, WA: The Boeing Company.
Gertman, D. & Blackman, H.S., 1994. Human reliability and safety analysis data handbook Handbook. New York: John Wiley and Sons.
Gianni, P., 2006. Nuclear Safety. Seattle, WA: The Boeing Company.
Hixenbaugh, A.F., 1968. Fault Tree for Safety. Seattle, WA: The Boeing Company.
Launer, L.J., 2005. Severe Accident Risks: An Assessment for Five U.S. Nuclear Power Plants, WA: The Boeing Company.
Lindsay, J., 1997. Fault Tree Analysis Program Plan. Seattle, WA: The Boeing Company.
Rechard, P., 1999. Historical Relationship between Performance Assessment for Radioactive Waste Disposal and Other Types of Risk Assessment in the United States. Risk Analysis, (Springer Netherlands), 19(5), p.763807.