Introduction
Rotational motion apparatus entails a shaft through which a threaded rod is mounted. Metal is cylintounted on the threaded rod, and string is wrapped around the shaft to apply a force to cause the system to rotate. The string is placed over a pulley so that force applied is from a vertically hanging mass.
Theory
The mass appears to push outward due to its inertia in the case of a spinning system because the centripetal force pulls the mass inward to follow a curved path. But in each of these instances, there is only one actual force at work, and the other is merely an appearance. The mass appears to push outward due to its inertia in the case of a spinning system because the centripetal force pulls the mass inward to follow a curved path. But in each of these instances, there is only one actual force at work, and the newton’s merely an appearance. The rem majorly applies the law of newton’s first law which states that force equals mass times acceleration or F = ma. The radius (r) of this circle is equal to the mass (m) times the square of the velocity (V) modeling the Centripetal force (F), or r = mv^2/F.
Data Collection and Data Analysis
This modeling process requires a learner to carefully design and implement appropriate experiments to quantitatively generate the association between angular acceleration and the applied torque on the system. A good model Aisling always keeps one variable changing while another independent variable is constant. The purpose of this experiment is to develop quantitatively the link between the applied torque to the system and the angular acceleration. The mass, height, and time data from this experiment were gathered and used to calculate the torque and angular acceleration.
The following relationship was used to obtain acceleration:
User Data 1 User Data 2
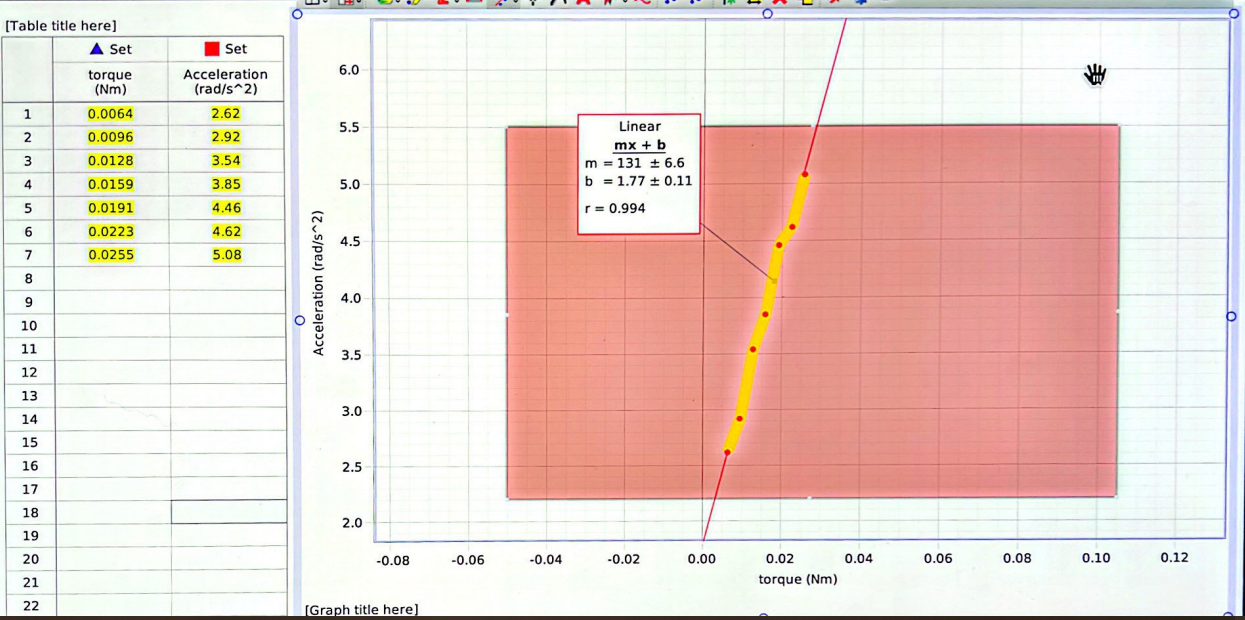
The graphical representation of the modeling process is a linear function, the equation of the graph is y=mx+b
m=131±6.6
b=1.77±0.11
r=0.994
The tension of the string at π rad/s2
Therefore π=3.142 from the graph tension will be 0.0099
The angular acceleration of the system is low due to the high effect of friction on the system. When measured value and value obtained from the model slightly differ due to environmental conditions that lower the efficiency of the practical. It results seem consistent with the model since the addition of mass will increase efficiency.
The value of the moment of inertia of the system is found by the slope that is:
m=131±6.6 Kg/m2 moment of inertia
Conclusion
A rotational system can be modeled in various ways and also graph to give a precise data presentation. The system applies the law of Newton’s second whereby the force is equal to the product of mass and acceleration. The resultant force is called centripetal force which is a force that results in a rotating mass. The rotating mass is pushed inwards by a centripetal force and keeps the mass on the path of a given radius. From the results obtained above, we can confidently conclude that the aim of this experiment was successfully achieved and the results obtained were by the theoretical expectations of the relationship between angular acceleration and torque. It was found that the angular acceleration and the torque have a linear relationship.
Reference
Morin, D. (2008). Introduction to Classical Mechanics. Cambridge University Press.